
|
|
|
Tipuri de modele economico-matematice
Modelele economico-matematice utilizate de intreprinderi in procesele economice se impart in doua categorii
Modele descriptive, care urmaresc reproducerea unor proprietati ale sistemului modelat
Modele normative, utilizate pentru aplicarea unor reguli eficiente de decizie in intreprindere cu scopul cresterii performantelor.
In practica, intre modelele descriptive si cele normative exista o intrepatrundere, deoarece majoritatea modelelor economico-matematice construite in intreprinderi au atat trasaturi descriptive, cat si trasaturi normative. Ceea ce le diferentiaza este ca unele sunt dominant descriptive, iar altele sunt dominant normative.
Distingerea intre cele doua aspecte (descriptiv si normativ) prezinta importanta pentru a evita confuzia dintre ceea ce exista si ceea ce dorim sa fie.
In raport de corespondenta dintre problemele economice si modelele economico-matematice, modelele descriptive pot fi grupate in
Modele ce surprind aspecte tehnologice si de productie
Modele informational-decizionale
Modele ale relatiilor umane;
Modele informatice.
1. Modele ce surprind aspecte tehnologice si de productie
In literatura de specialitate sunt prezentate o multitudine de modele privind aspectele tehnologice si de productie. Cateva dintre acestea sunt prezentate in continuare.
a) Modelul arborescent pentru descrierea structurii produselor si calculul necesarului de resurse materiale.
Cu ajutorul unui graf, modelul prezinta arborescenta unui produs P.
Arborescenta unui produs consta in partile componente ale produsului finit, cu precizarea normelor de consum retetei de fabricatie. Partile componente ale produsului se descriu pe mai multe niveluri, asfel incat, pe ultimul nivel sa poata fi citite componentele de baza, care descriu resursele materiale.
Exemplu
Consideram
PFi (i=1,.,p) - produsul finit;
ai (i=1,.,p) - cantitatile ce urmeaza a fi fabricate dinprodusul finit PFi
Cik - norma de consum din materialul MPk pentru produsul PFi
Nn - cantitatea necesara din materia prima n.
Pentru calculul necesarului de materii prime pe un singur nivel al arborescentei, vom avea
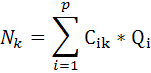
Pentru situatiile in care arborescenta este mai complicata pe mai multe niveluri, vom nota cu V - numarul de niveluri care intervin si cu h - rangul nivelului.
In acest caz, formula de calcul al necesarului de resurse materiale va fi
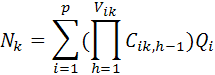
pentru k=![]()
Suma arata ca se vor aduna cantitatile pentru subproduse identice, fiind denumit calculul cu ajutorul exploziilor sumarizate.
Pe baza structurilor arborescente ale produselor finite se poate construi un model matriceal pentru determinarea necesarului de subansamble si componente, denumit modelul matricei exploziilor sumarizate.
Metoda de calcul consta in determinarea matricei
MES E+M1+M2+.+Mk
Unde: k numar niveluri de descompunere
M1 matricea initiala
E matricea unitate
Informatiile oferite de acest model arborescent sunt completate cu Fisa tehnologica a produsului, oferind astfel imaginea completa asupra structurii tehnologice a unui produs.
b) Modele tip grafice GANTT
Aceste modele sunt folosite in domeniile in care apare problema succesiunii in timp a unor activitati.
Pot fi folosite atat ca mocele descriptive, cat si ca modele normative, atunci cand este vorba despre secvente tehnologice.
c) Modele de tip ADC (Analiza Drumului Critic)
Graficele ADC reprezinta conditionarile logice si tehnologice dintre activitatile unui proiect si ofera posibilitatea luarii in considerare a necesarului de resurse materilae, umane si financiare.
Modelele de tip ADC ofera informatii utile cu privire la termenele de incepere si terminare a activitatiilor, rezerve, activitati critice, diagrame privind nivelarea, alocarea resurselor etc.
d) Modele de ordonantare si lotizare
Ordonantarea presupune stabilirea unei ordini de efectuare a activitatilor unui proces de productie, astfel ca interdependentele dintre ele sa fie respectate in limita resurselor deisponibile si cu o durata totala minima de executie.
Aceste modele se bazeaza pe tehnici combinatorice si pe procedee cunoscute sub denumirea branch-and-bound (ramifica si margineste).
Printre modelele clasice ale teoriei ordonantarii sunt: ordonantarea a n repere pe m masini (job shop), ordonantarea in flux (flow shop), algoritmi pentru ordonantarea cu restrictii de resurse limitate, modele de ordonantare bazate pe programarea liniara in numere intregi, modele ADC de tip euristic.
Alaturi de problemele de ordonantare se recomanda sa fie integrate si modelele de lot optim.
Modelele de ordonantare si lotizare constituie perspectiva moderna asupra programarii productiei.
e) Modele pentru determinarea capacitatilor de productie
Capacitatea de productie a unei intreprinderi se stabileste pe baza fondului de timp disponibil al utilajelor.
Modelele utilizate pentru determinarea capacitatilor de productie sunt modele complexe, deoarece se utilizeaza mai multi indicatori fizici si valorici, cum ar fi: fondul tehnic de timp pe grupe de masini, valoarea cifrei de afaceri, volumul productiei exprimat in unitati fizice, fondul de timp necesar pentru principalele piese de schimb etc.
Cu ajutorul acestor indicatori se exprima situatia tehnico-economica a intreprinderii la un moment dat (caracter descriptiv). Se poate formula un model de programare liniara cu mai multe functii obiectiv, incluzand astfel si aspecte normative.
Capacitatea de productie se poate optimiza din mai multe puncte de vedere reducerii consumului de materii prime sau de energie, al reducerii numarului de personal utilizat etc., in conditiile satisfacerii sentimentelor contractate si a unor costuri minime.
f) Modele pentru determinarea structurii de productie pe o perioada data
Aceste modele urmaresc determinarea unei structuri de productie, pe o perioada data, in functie de cerintele pietei (contracte incheiate) si de resursele disponibile pentru maximizarea sau minimizarea, dupa caz, a unor functii obiectiv, ca de exemplu: maximizarea profitului, minimizarea costului de productie, maximizarea cifrei de afaceri etc.
Consideram
Pj(j=1,n) - produsele care pot fi realizate intr-o intreprindere incantitatile xj
bi(i=1,m) - resursele disponibile (capacitati de productie, materii prime, materiale, muncitori, specialisti);
aij(i=1,.,m; j=1,.,n) - coeficienti tehnologici ai capacitatilor de productie, norme de materiale si de munca
P'j, P''j - limita inferioara, respectiv, limita superioara ce urmeaza a se fabrica din fiecare produs j, impuse de cerintele pietei
Crj - coeficientul variatiei xj fin functia obiectiv cu h=1,.,r pentru cele r functii obiectiv luate in considerare.
Modelul va fi
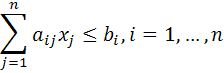
![]()
![]()
Opt
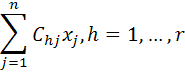
Acesta este un model de programare liniara cu mai multe functii obiectiv, in care restrictiile reprezinta partea descriptiva a modelului, iar functia obiectiv, partea normativa.
g) Modele pentru probleme de amestec
Continutul unei probleme de amestec sau dieta poate fi formulat astfel:
Un produs final P are in componenta produsele Pj (j=1,.,n), care trebuie amestecate.
Produsul P are caracteristici calitative impuse si exprimate prin m indicatori I1, I2,., In de marime bi (i 1,., m)
aij - marimea indicatorilor pentru fiecare produs (i 1,.,n)
Eh - (h=1,.,r) - indicatori de eficienta ai fiecarui produs cu marimile Chj (h=1,.,r); (j=1,.,n), care, dupa caz, vor fi maximizati sau minimizati.
Modelul matematic este de forma
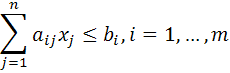
![]()
Opt
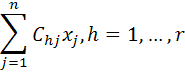
Si in cazul modelului de amestec, partea descriptiva a modelului o constituie restrictiile, iar partea normativa, functia obiectiv.
h) Modele de croire
In intreprinderi apar probleme de debitare (croire) a unor materiale uni sau bidimensionale (bare de otel, tevi, tabla, scanduri, stafe etc).
Modelul se bazeaza pe programarea matematica.
Consideram
aij - numarul de piese/bucati de tip i care se debiteaza/croiesc conform solutiei (tiparului) j
Cj - costul deseurilor ramane conform solutiei j
Ni - numarul de piese/bucati necesare de tip i
Xj numarul de suprafete debitate/croite conform solutiei j
Modelul general al problemei de croire va fi
![]()
![]()
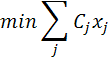
In practica, problemele de croire sunt rezolvate cu produse program specializate.
i) Modele de transport - repartitie
Aceste modele reprezinta cazuri particulare ale programarii liniare, care permit utilizarea unui algoritm de rezolvare.
Problema de transport, in general, consta in gasirea unui plan optim de transport al unui produs omogen, astfel incat, tinand seama de disponibilitatile furnizorilor si de cerintele clientilor, sa se minimizeze cheltuielile de transport sau numarul de t/km parcursi.
Daca notam cu
xij - cantitatea de marfa ce se transporta de la centrul de expeditie (furnizori) i la centrul de destinatie j
bj - necesarul la clientul j;
Cij - distanta sau costul asociat transportului unei unitati de produs de la furnizorul i la clientul j
ai - cantitetea disponibila la furnizorul i.
Modelul va fi
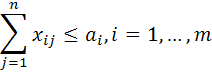
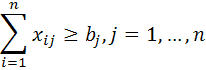
![]()
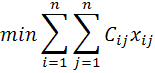
In acest caz, partea descriptiva a modelului o reprezinta restrictiile, iar partea normativa o reprezinta functia obiectiv.
j) Modele pentru probleme de afectare
Aceste modele se utilizeaza in urmatoarele situatii practice repartizarea muncitorilor pe masinile existente, a utilajelor pe lucrari, a specialistilor pe diverse sarcini complexe de cercetare/proiectare etc.
Pentru construirea modelului luam in considerare ca exista o multime de resurse M= care in procesul de productie trebuie afectate (repartizate) fiecare in parte, cate una din cele n resurse ale multimii N=.
Asfel iau nastere niste cupluri MiNj cu i=1, ., m si j=1, ., n, adica:
Muncitori pe masini
Utilaje pe lucrari
Specialisti pe sarcini de rezolvat etc.
Modelele cele mai utilizate in functie de specificul problemei sunt algoritmul ungar si metode de tip branch-and-bound (ramifica si margineste).
k) Modele de flux in retele de transport
Cu ajutorul acestor modele pot fi rezolvate urmatoarele tipuri de probleme din practica: se poate descrie procesul transportului intern intr-ouzina, distributia unei materii prime fluide sau gazoase (apa, CH4, abur, titei etc.) in procesul de productie etc.
Reteaua de transport este reprezentata de un graf, cu sau fara circuite, in care fiecarui arc XiXj i se asociaza o capacitate Cij, care reprezinta fluxul maxim care poate strabate o portiune din retea, reprezentata de arcul XiXj.
Problema consta in maximizarea fluxului total efectiv care strabate reteaua, cu respectarea restrictiilor de capacitate.
In general, pentru rezolvare se foloseste algoritmul Ford-Fulkerson.
l) Modele pentru amplasarea utilajelor
Amplasarea utilajelor in sectiile de productie trebuie facuta in asa fel, incat drumul parcurs de piesele care se prelucreaza sa fie cat mai redus, introducand pentru aceasta un indicator de eficienta.
Problema are doua parti, si anume
O parte descriptiva, care consta in caracterizarea tuturor utilajelor din punct de vedere al posibilitatii de prelucrare a reperelor
O parte normativa, care consta in intocmirea algoritmilor pentru formarea liniilor tehnologice si amplasarea propriu-zisa a utilajelor in cadrul acestora.
Caracterizarea utilajelor se face cu o matrice booleana de dimensiuni m x n (m= numarul reperelor, n= numarul utilajelor), cu ajutorul careia se pune in evidenta posibilitatea de a prelucra reperul Ri (i=1, ., m) pe masna Mj (j=1, ., n).
m) Modele pentru descrierea muncii fizice
Metodele mai importante de modelare descriptiva a muncii fizice au ca obiectiv sa ofere o imagine cat mai fidela a modului cum se efectueza munca fizica pentru ca pe baza acesteia sa se elaboreze modele normative.
Din categoria modelelor pentru descrierea muncii fizice fac parte si studiile ergonomice privind interactiunea dintre om si mediul de munca.
n) Modele pentru fenomene de asteptare
In activitatea practica din domeniul economic apar adesea situatii de asteptare, generate de imposibilitatea de a corela temporal diverse activitati care se interconditioneaza.
Conceperea unui model de asteptare presupune cunoasterea unor caracteristici ale fenomenului studiat privind numarul mediu de: unitati in sistem, a unitatilor in curs de servire, de unitati in sirul de asteptare, de statii neocupate, de unitati ce sosesc intr-o unitate de timp data, precum si timpul mediu: de servire, de asteptare in sistem si de asteptare in sir.
Aceste modele au un caracter complex descriptiv-normativ.
o) Modele de stocare
Avand in vedere ca stocarea presupune cheltuieli directe si indirecte generate de achizitionarea, transportul si depozitarea materiilor prime, materialelor etc, si uneori de deprecierea acestora, este oportun sa se utilizeze un program optim de productie, care sa asigure un nivel minim a cheltuielilor ocazionate de depozitare.
Sistemele moderne de gestiune a stocurilor raspund urmatoarelor cerinte
Determinarea cantitatii optime de comandat
Determinarea perioadei de aprovizionat (moment optim de lansare a comenzii de aprovizionare)
Determinarea stocului de siguranta optim in conditiile minimizarii cheltuielilor.
Modelul economico-matematic de stocare cuprinde principalele elemente ale oricarui proces de stocare, si anume cererea, aprovizionarea, parametrii temporali si costurile specifice (cost de lansare a unei comenzi, cost de stocare si cost de penalizare sau rupere).
Daca notam cu
![]() consumul de material m, la momentul t pentru a
obtine o cantitate din produsul i
consumul de material m, la momentul t pentru a
obtine o cantitate din produsul i
Xi - cantitatea de produs i exprimata in unitati fizice;
![]() stocul din materialul m existent la momentul t.
stocul din materialul m existent la momentul t.
Daca ![]()
Atunci ![]()
Asa incat ![]()
Componenta ∆S trebuie determinata cu modelele economico-matematice.
Exista o multitudine de modele de stocare deterministe, probabiliste, statice, dinamice, cu cerere continua, cu cerere discontinua etc.
Modelele de stocare cuprind atat elemente descriptive, cat si o parte normativa procesul de determinare a politicii optime de reaprovizionare.
p) Modele ale controlului static al calitatii produselor
Aceste modele au atat caracter descriptiv cat si normativ si se bazeaza pe cunostinte de statistica matematica.
2. Modele infomational-decizionale
Modelele informational-decizionale se impart in doua categorii
Modele pentru descrierea retetei informational-decizionale
Modele care descriu structura procesului decizional.
Din prima categorie fac parte
Modele de tip organigrama a structurii organizatorice
Diagrama de flux a documentelor
Diagrama informational-decizionala
Modelele de tip aval-amonte.
Din cea de-a doua categorie fac parte
a) Modele logicii formale, si anume
Modelele logicii clasice
Modelele logicii matematice
Modelele axiomatizate
Modelele metateoretice
Modelele semiotice
b) Metode ale teoriei deciziei, si anume
Modelul general al procesului decizional care expliciteaza elementele acestui proces variante, consecinte, criterii, stari ale naturii
Modelul deciziilor de grup a lui Arrow
Teoria utilitatii
Modele in conditii de risc si incertitudine
Modele multicriteriu.
1.5.3. Modele ale relatiilor umane
Modelarea descriptiva a relatiilor umane din intreprinderi se refera la conditiile observarii, obiectul observarii (indivizi, grupuri si resatiile lor reciproce) si masurarea rezultatelor observatiilor.
Printre modelele de descriere a relatiilor interpersonale si de grup se afla: interviul, chestionarul, autochestionarul.
Principalele modele de descriere a relatiilor interpersonale si de grup in intreprinderi sunt:
Testele sociometrice;
Modele pentru descrierea comunicarii intre indivizi si grupuri
Modele de simulare a relatiilor umane.
Un loc important il ocupa modelele descriptive in vederea selectiei si promovarii personalului (teste de inteligenta, de aptitudini speciale, de performanta) si modele care descriu comportamentul in intreprindere.
O prima categorie de modele incearca sa surprinda relatia dintre motivatii (trebuinte, tendinte, afecte, interese, interventii, idealuri) si comportament, cum ar fi importanta rolului profesional in procesul muncii pentru orice om.
Alte modele se refera la stilul de conducere al liderilor formali sau informali.
Pentru relatiile umane din intreprinderi exista o serie de modele pur normative, si anume
Modelul conducerii descentralizate a intreprinderii
Regula stimularii lucratorilor si specialistilor
Prioritatea relatiilor de respect si incredere fata de cele de autoritate
Regula responsabilitatii profesionale.
1.5.4. Modele informatice
Modelele informatice pot fi grupate in
Modele complexe hardware
Modele de tip software de aplicatii
Modele de organizare a datelor (fisiere, banci, baze de date).
Avand in vedere ca majoritatea modelelor economico-matematice au atat trasaturi descriptive, cat si normative, difera fiind doar intensitatea unora sau altora in situatia modelata, la un moment dat, se poate pune in evidenta zona de interferenta a lor printr-un modul de legatura (Fig. 2.2.).
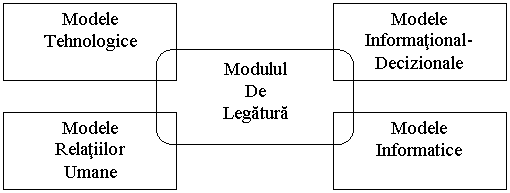
Fig. 2.2. Cele patru categorii de modele si modul de legatura