Metode de dezvoltare a creativitatii specifice matematicii

Metode de dezvoltare a creativitatii specifice matematicii

1. Natura creativitatii

In sens larg, creativitatea este un concept care se refera la potentialul de care dispune o persoana pentru a desfasura o activitate creatoare.

Activitatea creatoare este una dintre formele fundamentale ale activitatii omului (alte forme fiind jocul, invatarea, munca si comunicarea). Se deosebeste de celelalte forme de activitate umana prin caracteristicile produselor in care se concretizeaza si prin procesualitatea psihica ce ii este caracteristica.

Produsele activitatii creatoare intrunesc o serie de atribute specifice: noutate, originalitate, ingeniozitate, utilitate si valoare sociala.

Din punctul de vedere al structurilor psihologice implicate, creativitatea este o dimensiune integrala a personalitatii subiectului creativ: presupune imaginatie, dar nu se reduce la procesele imaginative; implica inteligenta, dar nu orice persoana inteligenta este si creatoare; presupune motivatie si vointa, dar nu poate fi explicata doar prin aceste aspecte etc.

Ca proces, creativitatea este legata de rezolvarea de probleme, insa persoana creatoare este cea care descopera noi probleme, pentru care nu exista o strategie rezolutiva anterioara, caci problema nu poate fi incadrata intr-o clasa cunoscuta de probleme.

2. Strategii pedagogice de stimulare a creativitatii elevilor

Dezvoltarea potentialului creativ uman presupune, in primul rand, o optima interactiune educativa a tuturor factorilor de educatie care interactioneaza intr-o societate, scoala nefiind singurul factor de influenta. Sunt necesar actiuni concertate in trei planuri distincte: a) social; b) individual- psihologic; c) calitatea vietii.

In plan social, de o deosebita importanta pentru descatusarea energiilor creatoare umane sunt preocuparile de a asigura (1) o larga participare democratica si creativa la procesele decizionale care privesc viata oamenilor; (2) aprecierea sociala a muncii creative si a persoanelor creative de catre societate; (3) crearea unor posibilitati reale cetateanului de a-si petrece timpul liber prin desfasurarea unor activitati creative, dupa preferinta s.a.

In plan individual psihologic, prezinta importanta: (1) crearea unui sistem eficient de instruire si educatie permanenta; (2) ridicarea calitatii educatiei si invatamantului; (3) preocupari sistematice de calificare a oamenilor; (4) educatia pentru creativitate s.a.

In ceea ce priveste calitatea vietii se impune crearea unor conditii favorabile unui regim de munca igienic, de natura sa sustina fizic efortul creator.

In contextul tuturor acestor conditii social-educative ale creativitatii, scoala urmeaza sa realizeze finalitati educative specifice, de care este direct responsabila. Ei ii revine responsabilitatea de a actiona pentru stimularea potentialului creativ al elevilor in urmatoarele directii:

• identificarea potentialului creativ al elevilor;
• crearea premiselor gnoseologice ale activitatii creatoare, libere si constiente a omului (o conceptie despre lume care sa dea sens si sa orienteze activitatea creativa);
• dezvoltarea posibilitatilor individuale de comunicare, care sa inlesneasca punerea rezultatelor creatiei la dispozitia societatii;
• dinamizarea potentialului creativ individual, in sensul valorificarii adecvate a talentelor si a cultivarii unor atitudini creative in special a acelor care constituie principalii factori vectoriali ai creativitatii;
• asigurarea suportului etic al comportamentului creator.

Cata vreme creatia era socotita un privilegiu dobandit ereditar de o minoritate, scoala nu s-a ocupat in mod special de acest aspect, desi, e drept, s-au creat ici colo clase speciale pentru supradotati. De cand se arata ca automatele dirijate de calculatoare infaptuiesc toate muncile monotone, stereotipe si deci omului ii revin mai mult sarcini de perfectionare, de innoire, cultivarea gandirii inovatoare a devenit o sarcina importanta a scolilor de masa. Pe langa efortul traditional de educare a gandirii critice, stimularea fanteziei apare si ea ca un obiectiv major. Aceasta implica schimbari importante, atat in mentalitatea profesorilor, cat si in ce priveste metodele de educare si instruire.

In primul rand, trebuie schimbat climatul, pentru a elimina blocajele culturale si emotive, puternice in scoala din trecut. Se cer relatii distinse, democratice, intre elevi si profesori, ceea ce nu inseamna a cobora statutul social al celor din urma. Apoi, modul de predare trebuie sa solicite participarea, initiativa elevilor, e vorba de acele metode active, din pacate prea putin utilizate in scoala romaneasca. In fine, fantezia trebuie si ea apreciata corespunzator, alaturi de temeinicia cunostintelor, de rationamentul riguros si spiritul critic.

In cele ce urmeaza, prezentam cateva metode de dezvoltare a creativitatii  care

se pot folosi in cadrul orelor de matematica: brainstorming, metoda mozaicului, metoda cubului, turul galeriei, ciorchinele.

3. Brainstorming

Brainstormingul este o metoda care ajuta la crearea unor idei si concepte creative si inovatoare. Pentru un brainstorming eficient, inhibitiile si criticile suspendate vor fi puse de-o parte. Astfel exprimarea va deveni libera si participantii la un proces de brainstorming isi vor spune ideile si parerile fara teama de a fi respinsi sau criticati. Un brainstorming dureaza in jur de o jumatate de ora si participa in medie 10 elevi sau grupuri de minim 10 elevi. Se expune un concept, o idee sau o problema si fiecare isi spune parerea despre cele expuse si absolut tot ceea ce le trece prin minte, inclusiv idei comice sau inaplicabile. O varianta a brainstormingului este brainwritingul.

O sesiune de brainstorming bine dirijata da fiecaruia ocazia de a participa la dezbateri si se poate dovedi o actiune foarte constructiva.

Etapele unui brainstorming eficient sunt urmatoarele: deschiderea sesiunii de brainstorming, o perioada de acomodare de 5-10 minute, partea creativa a brainstormingului, prelucrarea ideilor si stabilirea unui acord.

In deschiderea sesiunii de brainstorming se prezinta scopul acesteia si se discuta tehnicile si regulile de baza care vor fi utilizate.

Perioada de acomodare dureaza 5-10 minute si are ca obiectiv introducerea grupului in atmosfera brainstormingului. Este o mini-sesiune de brainstorming unde participantii sunt stimulati sa discute idei generale pentru a putea trece la un nivel superior.

Partea creativa a brainstormingului are o durata de 25-30 de minute. Este recomandabil ca in timpul derularii acestei etape, coordonatorul (profesorul) sa aminteasca timpul care a trecut si cat timp a mai ramas. Sa "preseze" participantii si in finalul partii creative sa mai acorde cate 3-4 minute in plus. In acest interval de timp grupul participant trebuie sa fie stimulati sa-si spuna parerile fara ocolisuri.

La sfarsitul partii creative coordonatorul brainstormingului clarifica ideile care au fost notate si puse in discutie si verifica daca toata lumea a inteles punctele dezbatute. Este momentul in care se vor elimina sugestiile prea indraznete si care nu sunt indeajuns de pertinente. Se face si o evaluare a sesiunii de brainstorming si a contributiei fiecarui participant la derularea sesiunii. Pot fi luate in considerare pentru evaluare: talentele si aptitudinile grupului, repartitia timpului si punctele care au reusit sa fie atinse.

Pentru a stabili un acord obiectiv cei care au participat la brainstorming isi vor spune parerea si vor vota cele mai bune idei. Grupul supus la actiunea de brainstorming trebuie sa stabileasca singuri care au fost ideile care s-au pliat cel mai bine pe conceptul dezbatut.

Pe timpul desfasurarii brainstormingului participantilor nu li se vor cere explicatii pentru ideile lor. Aceasta este o greseala care poate aduce o evaluare prematura a ideilor si o ingreunare a procesului in sine.

Metoda creativa denumita brainstorming are o lunga istorie, dar ea a fost reactivata de profesorul Alex Osborne, prorector la Universitatea Buffalo si fondator al Institutului de Creatie Tehnica, USA.

Fiecare dintre noi este o persoana creativa sau are anumite laturi creative. De multe ori ideea este "omorata" chiar de catre creatorul ei de frica infruntarii criticilor colegilor sai, de teama de a nu se face de ras. Autocritica distruge momentul in care o idee creativa este irosita inainte de a prinde viata. Brainstormingul functioneaza dupa principiul: asigurarea calitatii prin cantitate si isi propune sa elimine exact acest neajuns generat de autocritica.

Va recomandam 7 reguli pe care elevii le vor respecta in scopul unei sedinte reusite de brainstorming:

1. Nu judecati ideile celorlalti - cea mai importanta regula.

2. Incurajati ideile nebunesti sau exagerate.

3. Cautati cantitate, nu calitate in acest punct.

4. Notati tot.

5. Fiecare elev este la fel de important.

6. Nasteti idei din idei.

7. Nu va fie frica de exprimare.

Exemplul 1. Aplicarea metodei brainstorming la rezolvarea unei probleme

de geometrie la clasa a VII-a (a se vedea Anexa1).

Este important de retinut ca obiectivul fundamental al metodei brainstorming

consta in exprimarea libera a opiniilor prin eliberarea de orice prejudecati. De aceea, acceptati toate ideile, chiar traznite, neobisnuite, absurde, fanteziste, asa cum vin ele in mintea elevilor, indiferent daca acestea conduc sau nu la rezolvarea problemei. Pentru a determina progresul in invatare al elevilor este necesar sa ii antrenati in schimbul de idei; faceti asta astfel incat toti elevii sa isi exprime opiniile!

4. Mozaicul (Metoda Jigsaw)

Jigsaw (in engleza jigsaw puzzle inseamna mozaic) sau "metoda grupurilor

interdependente" este o strategie bazata pe invatarea in echipa (team-learning). Fiecare elev are o sarcina de studiu in care trebuie sa devina expert. El are in acelasi timp si responsabilitatea transmiterii informatiilor asimilate, celorlalti colegi.

In cadrul acestei metode rolul profesorului este mult diminuat, el intervine semnificativ la inceputul lectiei cand imparte elevii in grupurile de lucru si traseaza sarcinile si la sfarsitul activitatii cand va prezenta concluziile activitatii.

Exista mai multe variante ale metodei mozaic iar noi vom prezenta varianta standard a acestei metode care se realizeaza in cinci etape.

1. Pregatirea materialului de studiu

• Profesorul stabileste tema de studiu si o imparte in 4 sau 5 sub-teme. Optional,

poate stabili pentru fiecare sub-tema, elementele principale pe care trebuie sa puna accentul elevul, atunci cand studiaza materialul in mod independent. Acestea pot fi formulate fie sub forma de intrebari, fie afirmativ, fie un text eliptic care va putea fi completat numai atunci cand elevul studiaza materialul.

• Realizeaza o fisa-expert in care trece cele 4 sau 5 sub-teme propuse si care va

fi oferita fiecarui grup.

2. Organizarea colectivului in echipe de invatare de cate 4-5 elevi (in functie de numarul lor in clasa)

• Fiecare elev din echipa, primeste un numar de la 1 la 4-5 si are ca sarcina sa

studieze in mod independent, sub-tema corespunzatoare numarului sau.

• El trebuie sa devina expert in problema data. De exemplu, elevii cu numarul 1

din toate echipele de invatare formate vor aprofunda sub-tema cu numarul 1. Cei cu numarul 2 vor studia sub-tema cu numarul 2, si asa mai departe.

• Faza independenta: fiecare elev studiaza sub-tema lui, citeste textul

corespunzator. Acest studiu independent poate fi facut in clasa sau poate constitui o tema de casa, realizata inaintea organizarii mozaicului.

3. Constituirea grupului de experti

• Dupa ce au parcurs faza de lucru independent, expertii cu acelati numar se

reunesc, constituind grupe de experti pentru a dezbate problema impreuna. Astfel, elevii cu numarul 1, parasesc echipele de invatare initiale si se aduna la o masa pentru a aprofunda sub-tema cu numarul 1. La fel procedeaza si ceilalti elevi cu numerele 2, 3, 4 sau 5. Daca grupul de experti are mai mult de 6 membri, acesta se divizeaza in doua grupe mai mici.

• Faza discutiilor in grupul de experti: elevii prezinta un raport individual

asupra a ceea ce au studiat independent. Au loc discutii pe baza datelor si a materialelor avute la dispozitie, se adauga elemente noi si se stabileste modalitatea in care noile cunostinte vor fi transmise si celorlati membrii din echipa initiala.

• Fiecare elev este membru intr-un grup de experti si face parte dintr-o echipa

de invatare. Din punct de vedere al aranjamentului fizic, mesele de lucru ale grupurilor de experti trebuie plasate in diferite locuri ale salii de clasa, pentru a nu se deranja reciproc.

• Scopul comun al fiecarui grup de experti este sa se instruiasca cat mai bine,

avand responsabilitatea propriei invatari si a predarii si invatarii colegilor din echipa initiala.

4. Reintoarcerea in echipa initiala de invatare

• Faza raportului de echipa: expertii transmit cunostintele asimilate, retinand la

randul lor cunostintele pe care le transmit colegii lor, experti in alte sub-teme. Modalitatea de transmitere trebuie sa fie scurta, concisa, atractiva, putand fi insotita de suporturi audio-vizuale, diverse materiale.

• Specialistii intr-o sub-tema pot demonstra o idee, citi un raport, folosi

computerul, pot ilustra ideile cu ajutorul diagramelor, desenelor, fotografiilor. Membrii sunt stimulati sa discute, sa puna intrebari si sa-si noteze, fiecare realizandu-si propriul plan de idei.

5. Evaluarea

• Faza demonstratiei: grupele prezinta rezultatele intregii clase. In acest moment

elevii sunt gata sa demonstreze ce au invatat. Profesorul poate pune intrebari, poate cere un raport sau un eseu ori poate da spre rezolvare fiecarui elev o fisa de evaluare. Daca se recurge la evaluarea orala, atunci fiecarui elev i se va adresa o intrebare la care trebuie sa raspunda fara ajutorul echipei.

Exemplul 2. Aplicarea metodei mozaicului la predarea unei lectii de

aritmetica la clasa a V-a (a se vedea Anexa 2).

Ca toate celelalte metode de invatare prin cooperare si aceasta presupune urmatoarele avantaje:

stimularea increderii in sine a elevilor;

dezvoltarea abilitatilor de comunicare argumentativa si de relationare in cadrul grupului;

dezvoltarea gandirii logice, critice si independente;

dezvoltarea raspunderii individuale si de grup;

optimizarea invatarii prin predarea achizitiilor altcuiva.

"Trebuie sa remarcam calitatea metodei grupurilor interdependente de a

anihila manifestarea efectului Ringelmann. Lenea sociala, cum se mai numeste acest efect, apare cu deosebire atunci cand individul isi imagineaza ca propria contributie la sarcina de grup nu poate fi stabilita cu precizie. Interdependenta dintre membri si individualizarea aportului fac din metoda Jigsaw un remediu sigur impotriva acestui efect".

5. Metoda cubului

Metoda cubului presupune explorarea unui subiect, a unei situatii din mai multe perspective, permitand abordarea complexa si integratoare a unei teme.

Sunt recomandate urmatoarele etape:

Realizarea unui cub pe ale carui fete sunt scrise cuvintele: descrie, compara,

analizeaza, asociaza, aplica, argumenteaza.

Anuntarea temei, subiectului pus in discutie.

Impartirea clasei in 6 grupe, fiecare dintre ele examinand tema din perspectiva

cerintei de pe una din fetele cubului.

Descrie: culorile, formele, marimile, etc.

Compara: ce este asemanator? Ce este diferit?

Analizeaza: spune din ce este facut, din ce se compune.

Asociaza: la ce te indeamna sa te gandesti?

Aplica: ce poti face cu aceasta? La ce poate fi folosita?

Argumenteaza: pro sau contra si enumera o serie de motive care vin in sprijinul afirmatiei tale.

Redactarea finala si impartasirea ei celorlalte grupe.

Afisarea formei finale pe tabla sau pe peretii clasei.

Exemplul 3. La lectia de recapitulare si sistematizare a cunostintelor

- Unitatea de invatare: Divizibilitatea numerelor naturale - clasa a VI-a, am folosit metoda cubului si turul galeriei (a se vedea Anexa 3).

6. Turul galeriei

Turul galeriei este o metoda interactiva de invatare bazata pe colaborarea

intre elevi, care sunt pusi in ipostaza de a gasi solutii de rezolvare a unor probleme. Aceasta metoda presupune evaluarea interactiva si profund formativa a produselor realizate de grupuri de elevi.

Astfel, turul galeriei consta in urmatoarele:

1. Elevii, in grupuri de trei sau patru, rezolva o problema (o sarcina de invatare)

susceptibila de a avea mai multe solutii (mai multe perspective de abordare).

2. Produsele muncii grupului se materializeaza intr-o schema, diagrama, inventar

de idei etc. notate pe o hartie (un poster).

3. Posterele se expun pe peretii clasei, transformati intr-o veritabila galerie.
4. La semnalul profesorului, grupurile trec pe rand, pe la fiecare poster pentru a

examina solutiile propuse de colegi. Comentariile si observatiile vizitatorilor sunt scrise pe posterul analizat.

5. Dupa ce se incheie turul galeriei (grupurile revin la pozitia initiala, inainte de

plecare) fiecare echipa isi reexamineaza produsul muncii lor comparativ cu ale celorlalti si discuta observatiile si comentariile notate de colegi pe propriul poster.

Turul galeriei se foloseste cu succes impreuna cu metoda cubului asa cum se poate vedea si in exemplul 3 prezentat anterior.

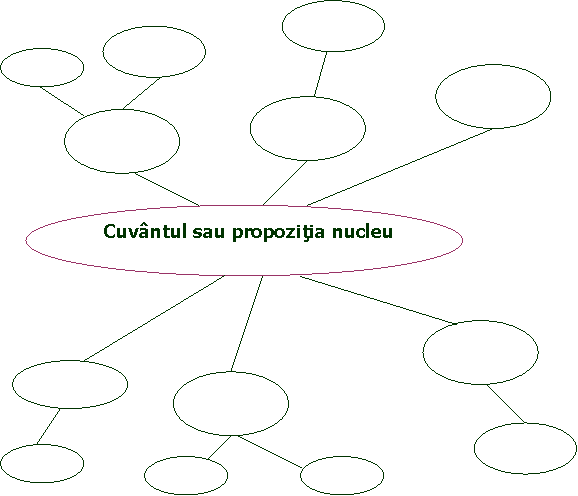
7. Ciorchinele

Desi este o varianta mai simpla a brainstorming-ului, ciorchinele este o

metoda care presupune identificarea unor conexiuni logice intre idei, poate fi folosita cu succes atat la inceputul unei lectii pentru reactualizarea cunostintelor predate anterior, cat si in cazul lectiilor de sinteza, de recapitulare, de sistematizare a cunostintelor.

Ciorchinele este o tehnica de cautare a cailor de acces spre propriile cunostinte evidentiind modul de a intelege o anumita tema, un anumit continut.

Ciorchinele reprezinta o tehnica eficienta de predare si  invatare care incurajeaza elevii sa gandeasca liber si deschis.

Metoda ciorchinelui functioneaza dupa urmatoarele etape:

1. Se scrie un cuvant / tema (care urmeaza a fi cercetat) in mijlocul tablei sau a

unei foi de hartie.

2. Elevii vor fi solicitati sa-si noteze toate ideile, sintagmele sau cunostintele pe

care le au in minte in legatura cu tema respectiva, in jurul cuvantului din centru, tragandu-se linii intre acestea si cuvantul initial.

3. In timp ce le vin in minte idei noi si le noteaza prin cuvintele respective, elevii

vor trage linii intre toate ideile care par a fi conectate.

4. Activitatea se opreste cand se epuizeaza toate ideile sau cand s-a atins limita

de timp acordata.

Exista cateva reguli ce trebuie respectate in utilizarea tehnicii ciorchinelui:

Scrieti tot ce va trece prin minte referitor la tema / problema pusa in discutie.

Nu judecati / evaluati ideile produse, ci doar notatiile.

Nu va opriti pana nu epuizati toate ideile care va vin in minte sau pana nu expira timpul alocat; daca ideile refuza sa vina insistati si zaboviti asupra temei pana ce vor aparea unele idei.

Lasati sa apara cat mai multe si mai variate conexiuni intre idei; nu limitati nici numarul ideilor, nici fluxul legaturilor dintre acestea.

Avantajele acestei tehnici de invatare sunt:

• In etapa de reflectie vom utiliza "ciorchinele revizuit" in care elevii vor fi ghidati prin intermediul unor intrebari, in gruparea informatiilor in functie de anumite criterii.

• Prin aceasta metoda se fixeaza mai bine ideile si se structureaza infomatiile facilizandu-se retinerea si intelegerea acestora.

• Adesea poate rezulta un "ciorchine" cu mai multi "sateliti".

Exemplul 4. Aplicarea metodei ciorchinelui la rezolvarea unei probleme de

geometrie la  clasa a VII-a (a se vedea Anexa 4).

BIBLIOGRAFIE

Ardelean L., Secelean N. - Didactica matematicii - notiuni generale,

comunicare didactica specifica matematicii, Ed. Universitatii Lucian

Blaga , Sibiu, 2007

Ardelean L., Secelean N. - Didactica matematicii - managementul,

proiectarea si evaluarea activitatilor didactice, Ed. Universitatii Lucian

Blaga , Sibiu, 2007

Dumitru I.A. Dezvoltarea gandirii critice si invatarea eficienta,

Ed. de Vest, Timisoara, 2000

Sarivan L. coord. - Predarea interactiva centrata pe elev, Educatia 2000+,

2005, Bucuresti, 2005

Singer M., Voica C. - Recuperarea ramanerii in urma la matematica,

Educatia 2000+, 2005, Bucuresti, 2005

ANEXE

Anexa 1. Aplicarea metodei brainstorming la rezolvarea unei probleme

de geometrie la clasa a VII-a.

Etape:

1. Alegerea sarcinii de lucru

Fie ABCD un patrulater convex, in care BC si AD nu sunt paralele, fie

EI(BC) si FI(AD) astfel incat . Construim paralelogramele ABEG si ECDH. Demonstrati ca:

a) AG DH; b) < GFA s < DFH; c) Punctele G, F, si H sunt coliniare;

d) EF este bisectoarea unghiului GEH.

(cf. Manual de matematica pentru clasa a VII-a, Ed. Teora, 2000)

2. Solicitarea exprimarii intr-un mod cat mai rapid, a tuturor ideilor legate de rezolvarea problemei. Sub nici un motiv, nu se vor admite referiri critice.

Cereti elevilor sa propuna strategii de rezolvare a problemei. Pot aparea, de

exemplu, sugestii legate de realizarea unei figuri cat mai corecte, de verificare "pe desen" a proprietatilor cerute in concluzia problemei, de masurare a unor unghiuri sau segmente. Lasati elevii sa propuna orice metoda le trece prin minte!

3. Inregistrarea tuturor ideilor in scris (pe tabla). Anuntarea unei pauze pentru asezarea ideilor (de la 15 minute pana la o zi).

Notati toate propunerile elevilor. La sfarsitul orei, puneti elevii sa transcrie

toate aceste idei si cereti-le ca pe timpul pauzei, sa mai reflecteze asupra lor.

4. Reluarea ideilor emise pe rand si gruparea lor pe categorii, simboluri, cuvinte cheie, etc.

Pentru problema analizata, cuvintele-cheie ar putea fi: masurare, congruenta,

asemanare, paralelism.

5. Analiza critica, evaluarea, argumentarea, contraargumentarea ideilor emise anterior. Selectarea ideilor originale sau a celor mai apropiate de solutii fezabile pentru problema supusa atentiei.

Puneti intrebari de tipul: Am putea rezolva problema folosind masuratori pe o

figura cat mai corecta? Este util sa studiem un caz particular al problemei? Au intrebarile problemei legatura intre ele? Ce anume trebuie sa demonstram?

6. Afisarea ideilor rezultate in forme cat mai variate si originale: cuvinte, propozitii, colaje, imagini, desene, etc.

Ca urmare a discutiilor avute cu elevii, trebuie sa rezulte strategia de rezolvare

a problemei. Aceasta poate fi sintetizata sub forma unor indicatii de rezolvare de tipul:

• construim figura;
• aplicam un criteriu de asemanare;
• folosim teorema bisectoarei.

Anexa 2. Aplicarea metodei mozaicului la predarea unei lectii de

aritmetica la clasa a V-a.

Etape:

1. Impartirea clasei in grupuri eterogene de 4 elevi, fiecare dintre acestia primind cate o fisa de invatare numerotata de la 1 la 4. Fisele cuprind parti ale unui material, ce urmeaza a fi inteles si discutat de catre elevi.

Propuneti lectia "Propozitii compuse" din Manualul de matematica pentru

clasa a V-a, Ed. Sigma, 2002. Cele patru fise de lucru sunt paragrafele prezentate in manual cu titlurile: Cand obtinem propozitii adevarate folosind "si" "sau" "nu" "daca.atunci."?.

2. Prezentarea succinta a subiectului tratat. Explicarea sarcinii de lucru si a modului in care se va desfasura activitatea.

In cazul analizat, subiectul analizat este "Propozitii compuse".

3. Regruparea elevilor, in  functie de numarul fisei primite, in grupuri de experti: toti elevii care au numarul 1 vor forma un grup, cei cu numarul 2 vor forma alt grup s.a.m.d.

Asadar, unul dintre grupurile de "experti" va fi format din toti elevii care au

primit, in cadrul grupului initial de 4, portiunea de lectie cu titlul: Cand obtinem propozitii adevarate folosind "si"?

4. Invatarea prin cooperare a sectiunii care a revenit fiecarui grup de experti. Elevii citesc, discuta, incearca sa inteleaga cat mai bine, hotarasc modul in care pot preda ceea ce au inteles colegilor din grupul lor originar.

Elevii din fiecare grup decid cum vor "preda". Ei pot folosi desene, exemple

numerice, texte in vorbirea curenta, simboluri matematice.

5. Revenirea in grupul initial si predarea sectiunii pregatite celorlalti membri. Daca sunt neclaritati, se adreseaza intrebari expertului. Daca neclaritatile persista se pot adresa intrebari si celorlalti membrii din grupul expert pentru sectiunea respectiva.

In fiecare grup, sunt astfel "predate" cele patru secvente ale lectiei. In acest

fel, fiecare elev devine responsabil atat pentru propria invatare, cat si pentru transmiterea corecta si completa a informatiilor. Este important sa monitorizati aceasta activitate, pentru ca achizitiile sa fie corect transmise.

6. Trecerea in revista a materialului dat prin prezentare orala cu toata clasa cu toti participantii.

Cateva intrebari bine alese de profesor vor evidentia nivelul de intelegere a

temei.

Metoda Mozaicului are avantajul ca implica toti elevii in activitate si ca fiecare dintre ei devine responsabil, atat pentru propria invatare, cat si pentru invatarea celorlalti. De aceea, metoda este foarte utila in motivarea elevilor: faptul ca se transforma, pentru scurt timp, in "profesori" le confera un ascendent moral asupra colegilor.

Anexa 3. La lectia de recapitulare si sistematizare a cunostintelor

- Unitatea de invatare: Divizibilitatea numerelor naturale - clasa a VI-a, am folosit metoda cubului si turul galeriei.

Am realizat un cub din carton si am colorat fiecare fata diferit, iar fiecarei fete
i-am asociat un verb, astfel:

Fata 4 - portocaliu

- verbul ANALIZEAZA

Fata 5 - galben

- verbul ARGUMENTEAZA

Fata 6 - mov

verbul APLICA