|
|
|
PROBLEME GENERALIZATE DE TRANSPORT
Prezentam in continuare cateva dintre cele mai reprezentative generalizari ale problemei de transport, mentionand de fiecare data aspectele deosebite pe care le ridica rezolvarea celor trei subprobleme mentionate mai sus si care le disting de problema standard.
1. PPOBLEMA DE TRANSPORT CU CENTRE INTERMEDIARE
Presupunem ca produsele realizate de 
producatori 
in
cantitatile 
respectiv, sunt transportate la 
depozite 
de
capacitati 
, produse ce
urmeaza a fi transportate la 
consumatori 
, care solicita
cantitatile 
, respectiv.
Daca 
sunt costurile de
transport ale unei unitati de produs de la 
la , iar 
sunt costurile unitare
de transport de la la 
se cere sa se
determine un plan optim de transport, adica valorile necunoscutelor 
ce reprezinta
cantitatile de produs ce urmeaza a fi transportate de la
producatorii la depozitele 
si ale
necunoscutelor 
ce reprezinta
cantitatile de produs ce urmeaza a fi transportate de la
depozitele la consumatorii .
Modelul problemei formulate este:
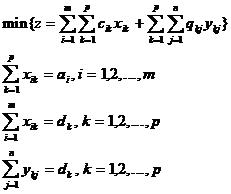(6)
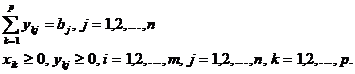
Modelul (6) este echivalent cu doua modele de tipul (1) si admite solutii in ipoteza ca sunt satisfacute conditiile:
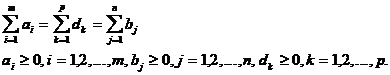(7)
Cele doua modele echivalente cu modelul (6) sunt (8) si (9).
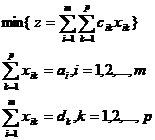(8)
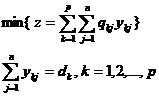(9)
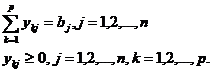
2. PROBLEMA DE TRANSPORT CU CAPACITATI LIMITATE
In multe situatii economice concrete capacitatile rutelor de transport sunt limitate, limitarile fiind impuse din diverse considerente tehnico-economice.
Modelul unei asemenea probleme este urmatorul:
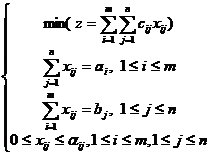(10) Echivalentul
relatiei (2) care asigura existenta programelor pentru problema
(10) sunt, de aceasta data, relatiile (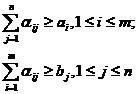11):
(11)
In acest caz subproblemele DPBI si TOPB comporta modificari, in timp ce subproblema IP ramane neschimbata.
Subproblema DPBI consta in atribuirea variabilei xpq a valorii 
cu mentiunea ca variabila xpq este considerata variabila de baza
numai in cazul in care 
sau 
.
Datorita restrictiilor 
este posibil ca vectorul 
sa nu fie
program, deoarece este posibil ca disponibilul de produs sa nu fie complet
epuizat, sau necesarul de produs sa nu fie complet satisfacut. Se
poate arata ca in conditiile (7) pornind de la programul 
se poate determina un program de baza. Presupunem
ca in centrul de productie Pk
a ramas neexpediata cantitatea de produs K, iar in centrele de consum Ch
si Cl sunt
necesare cantitatile H
respectiv L. Deoarece cererea este
egala cu oferta rezulta ca K
= H + L.
3. MODELE TRIDIMENSIONALE DE TRANSPORT
Problemele
de organizare optima a transporturilor necesare pentru aprovizionarea
consumatorilor cu mai multe produse diferite conduc la modele matematice ale
caror variabile sunt marcate cu trei indici. Presupunem ca
producatorii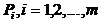 
dispun de produsele 
, solicitate de consumatorii 
. Daca se cunosc cantitatile:
cantitatea totala
de produse expediate de producatorul
, consumatorului 
;
cantitatea de produse 
, necesare consumatorului ;
cantitatea de produse 
, disponibile la
producatorul ;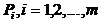
si se noteaza cu:
costul transportului
unei unitati de produs 
de la
producatorul 
la consumatorul 
;
cantitatea din
produsul primita de
consumatorul de la
producatorul ; modelul standard al problemei de transport tridimensionale
este urmatorul:
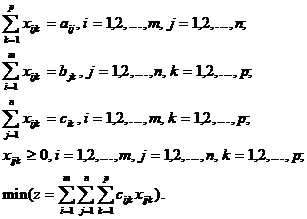(12)
Problema de transport al carei model este (12) admite programe daca sunt indeplinite conditiile 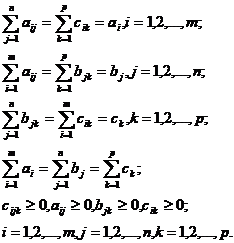(13):
(13)
