Modelarea problemelor de transport si aprovizionare

Modelarea problemelor de transport si aprovizionare

1.Retele de transport

1.1.Clasificarea problemelor de transport si aprovizionare

Graful asociat unei probleme clasice de transport este bipartit, nodurile care reprezinta furnizorii formeaza multimea S, iar nodurile corespunzatoare consumatorilor formeaza multimea T si se numeste retea de transport.

Pentru Cercetarea Operationala prezinta interes analiza problemelor de optim in retele de transport in urmatoarele ipoteze:

1.Cel putin o sursa poate aproviziona mai multe destinatii si cel putin o destinatie poate primi unitati de flux de la mai multe surse. Rutele de legatura pot avea si alte puncte comune in afara surselor si destinatiilor, acestea fiind numite puncte intermediare sau puncte de tranzit. Legaturile directe intre surse nu sunt excluse. In principiu, orice ruta poate fi parcursa in ambele sensuri, dar pot exista si rute cu sens unic.

50300

100

120

300

230 400

a) b)

destinatie sursa

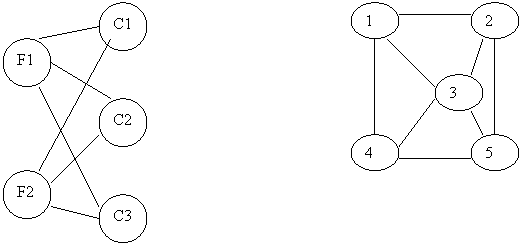
Figura 1.

Totalitatea surselor, destinatiilor, al punctelor de tranzit si al rutelor de legatura formeaza reteaua de transport. Ansamblul acesta care formeaza reteaua de transport se identifica cu un graf neorientat sau partial orientat(vezi figura 1.).

Unele rute de legatura pot avea limitari superioare si/sau inferioare pentru volumul unitatilor de flux ce se deplaseaza intr-un anumit sens. Aceste limitari poarta numele de capacitati ce pot fi inferioare respectiv superioare. In continuare vom lua in considerare numai cazul in care toate capacitatile inferioare sunt egale cu zero, iar cele superioare sunt exprimate prin numere pozitive.

3.Exista un cost al deplasarii unei unitati de flux de la un punct al retelei la altul, acest cost poate fi exprimat in bani timp sau distanta. In unele situatii acest cost poate semnifica profitul obtinut de pe urma deplasarii. Pe aceeasi ruta atat costurile cat si capacitatile pot diferi in functie de sensul de parcurgere.

Intotdeauna ipoteza 1. va fi presupusa in timp ce celelalte doua pot fiinta atat separat cat si simultan.

a)In prezenta ipotezei 3. si absenta ipotezei se pune problema deplasarii cantitatii de flux Q de la surse la destinatii la un cost total minim. Putem obtine problema clasica de transport in cazul in care sursele sunt in legatura directa cu destinatiile. Daca exista si puncte intermediare obtinem problema transferului. In cazul particular al unei singure surse S, al unei singure destinatii T si a unei singure unitati de flux se obtine problema drumului de cost minim de la S la T.

b)In prezenta ipotezei    si absenta ipotezei 3.se pune problema daca reteaua, ale carei rute sunt capacitate, este capabila sa permita acoperirea integrala a cererilor in punctele de destinatie. In cazul acesta vom folo si problema determinarii volumului maxim Q* de unitati de flux ce pot fi deplasate de la surse la destinatii. In cazul in care Q*<Q vor exista destinatii a caror cerere este acoperita partial si atunci se ridica problema maririi capacitatii de transfer a retelei.

c)In prezenta ambelor ipoteze se pune problema satisfacerii cererilor in punctele de destinatie la un cost de transport minim. Aceasta este problema fluxului (maxim) de cost minim.           

1.Problema clasica de transport si PTE

Un produs omogen se afla disponibil in localitatile F1, F2,,Fm in cantitatile a₁,a₂,,a_m si este cerut pentru consum in centrele b₁,b₂,,b_n.Se presupune cunoscut costul c_ij al transportului unei unitati de produs de la Fi la Cj. Se pune problema satisfacerii cererii in punctele de consum la un cost de transport minim.

Centrele furnizoare, cele consumatoare, legaturile directe intre ele si costurile unitare de transport sunt vizualizate de obicei printr-un graf orientat ca in figura 1.a).

Sub forma generala, un model liniar de tip transport poate fi scris astfel:

^{m n}

^{[opt]f=a acijxij}

^i=1j=1

_n

aX_ij ≤a_i, 1≤i≤m

_j=1

_m

ax_ij≥b_j, 1≤i≤n

_i=1

unde:

_{m n}

1) a ac_ijx_ij reprezinta fie costul total al operatiunii de tip transport (cand se

_i=1j=1

cere minimizarea acestuia), fie profitul total al operatiunii de tip transport (cand se cere maximizarea acestuia);

2)a_i reprezinta disponibilul furnizorului Di, 1≤i≤m;

3)b_j reprezinta necesarul consumatorului Cj, 1≤j≤n;

4)c_ij reprezinta costul unitar (sau profitul unitar) pe relatia (Di,Cj);

5)x_ij reprezinta cantitatea transportata de la furnizorul Di la consumatorul Cj, x=(x_ij), 1≤i≤m, 1≤j≤n;

6)restrictia _n

ax_ij ≤a_i,

_j=1

arata ca nu se pot aloca tuturor consumatorilor mai mult decat este disponibilul furnizorului Di;

7)restrictia _m

ax_ij≥b_j,

ⁱ⁼¹

arata ca de la toti furnizorii se aloca pentru consumul Cj cel putin cat este necesarul sau;

_m

8)a= aa_i, disponibilul (sau oferta) tuturor furnizorilor,

ⁱ⁼¹

_n

iar b=ab_j, necesarul (sau cererea) tuturor consumatorilor in

_j=1

ipoteza ca insumarile au sens.

Se spune ca o problema de transport este :

a)echilibrata daca oferta totalaa este egala cu cererea totala, adica

_{m n}

a= aa_i=ab_j=b.

^i=1j=1

b)neechilibrata daca oferta totala este diferita de cererea totala, adica

_{m n}

a= aa_i ab_j=b.

^i=1j=1

Conceptul de echilibrare este fundamental pentru construirea procedurilor de solutionare a unei probleme de tip transport.

In cazul PTE rezulta un tabel de forma:

Tabelul 1.

La problema de tip neechilibrat in scopul echilibrarii acesteia intalnim doua cazuri:

m n n m

1) Daca aq_i<ad_j, sfiind oferta, s = ad_j-aq_i, in scopul

i=1j=1 j=1 i=1

echilibrarii se introduce un consumator fictiv, de unde rezulta un tabel de forma :

Tabelul

m n mn

2) Dacaaq_i>ad_j, D fiind cererea, D=aq_i-ad_j,in

i=1 j=1i=1 j=1

scopul echilibrarii se introduce un furnizor fictiv, de unde rezulta un tabel de forma:

Tabelul 3.

In concluzie, rezulta ca orice problema de tip neechilibrat poate fi transformata in PTE.

1.3.Formalizarea problemei PTE

Posibilitati de rezolvare

Forma particulara a problemei de tip transport a condus la unele metode specifice relativ simple, de determinarea a solutiei de baza .

Cele mai folosite metode sunt:

-metoda costului minim pe ansamblu (tabel);

-metoda diferentelor maxime (VOGEL).

Metoda costului minim pe ansamblu (tabel)

Aceasta metoda consta din a aloca pentru fiecare pereche sau relatie (Di,Cj) a cantitatii x_ij egala cu minimul dintre cerere si oferta existente in momentul acelei alocari, procedeul se aplica pe tabel in ordinea crescatoare a costurilor unitare c_ij.

Metoda diferentelor maxime (VOGEl)

Aceasta este o metoda mai elaborata.

Presupunem costurile unitare de transport inscrise intr-un tabel cu m randuri si n coloane.

1)Pe fiecare rand si pe fiecare coloana a acestui tabel se calculeaza diferenta dintre cel mai mic cost de transport si cel imediat superior; daca costul minim nu este unic, diferenta se va lua egala cu zero.

2)Se identifica randul sau coloana cu cea mai mare diferenta si aici, in ruta de cost minim, se executa prima alocare din algoritmul precedent.

3)Se refac diferentele pe randurile si coloanele neblocate folosind numai costurile neblocate, dupa care se reia procedura de alocare.

Voi prezenta in continuare intr-o schema logica algoritmul de rezolvare a PTE.

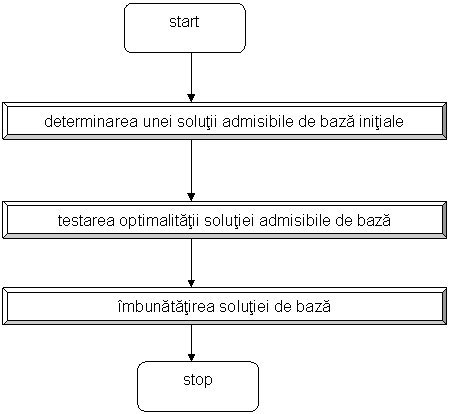Figura Schema logica a algoritmului de rezolvare a PTE prin metoda Simplex

1.4.Problema de transfer

In problema clasica de transport, sursele erau in legatura directa cu destinatiile, rutele erau orientate de la surse catre destinatii si nu era permis nici un transport intre doua surse sau intre doua destinatii. Problema de transfer este o generalizare a problemei clasice de transport in urmatoarele directii:

.In reteaua asociata exista si centre intermediare sau de tranzit ; pot exista legaturi intre surse sau destinatii; ca urmare,este posibil ca o sursa (o destinatie) sa 'functioneze' la un moment dat si ca punct de tranzit pentru unitati de flux provenind de la o alta sursa (sau care se deplaseaza catre o alta destinatie).

.Pe unele rute de transport pot fi efectuate in ambele sensuri,costul unitar al transportului putand depinde de sensul de parcurgere al rutei.

Diferentele existente intre retele asociate unei probleme aclasice de transport respectiv unei probleme de transfer sunt puse in evidenta in figura 1.

Modelul matematic al problemei de transfer

Problema de transfer se poate descrie in urmatorii termeni.

Exista n localitati, notate 1,2,,n si se pune problema organizarii transportului unui anumit produs omogen intre aceste localitati la un cost total minim. Intre unele localitati exista legaturi directe numite rute. Pe fiecare ruta este precizat un cost al transportului unei unitati de produs de la o extremitate la cealalta. Este posibil ca aceste costuri unitare sa depinda de sensul de parcurgere al rutei respective. Pentru uniformitatea expunerii vom presupune ca intre oricare doua localitati i si j exista o legatura directa accesibila in ambele sensuri, convenind ca daca o asemenea ruta sau sens de parcurgere nu exista in realitate, costul corespunzator sa fie luat egal cu +

Ansamblul localitatilor si al rutelor de legatura poarta numele de retea de transport si poate fi vizualizata printr-un graf finit, neorientat sau partial orientat, simplu si conex.

Nodurile retelei sunt diferentiate in:

-surse: localitati in care produsul este disponibil pentru a fi transportat in alte locuri;

-destinatii: localitati in care produsul este cerut pentru consum, cererea neputand fi acoperita din productia locala;

-centre intermediare (de tranzit): localitati in care produsul se gaseste doar in tranzit eventualul consum fiind asigurat din productia locala.

Pentru fiecare i=1,.,n vom nota:

-a_i, cantitatea disponibila in nodul i pentru a fi transportata spre alte localitati.Evident a_i>0 daca i este o sursa si a_i=0 in celelalte cazuri.

-b_i, cantitatea neta solicitata pentru consum in nodul i.Daca i este o destinatie atunci b_i>0, in celelalte noduri b_i=0.

-c_ij (undei j), costul transportului unei unitati de produs de la i la j.Vom presupune ca c_ij>0 si ca c_ij=+ in cazul in care deplasarea de la i la j nu este posibila in realitate.Pentru simplificarea notatiilor vom pune c_ij=0.

-x_ij (i j), cantitatea de produs transportata din nodul i in nodul j. Daca transportul de la i la j nu este permis conditia c_ij=+ va implica x_ij=0 in orice solutie admisibila a problemei.

-x_j, i= 1,.,n cantitatea de produs aflata in tranzit in nodul i (adica primita din unele localitati si expediata spre altele).

Putem atasa fiecarui nod al retelei de transport urmatoarele relatii:

n

ax_ik-x_ij=a_i , i=1,.,n(1)

k=1

k i

sau: Totalul unitatilor Cantitatatea aflata Productia

expediate din - in tranzit in= in nodul i

nodul inodul i (disponibila

spre a fi

expediata

catre alte

noduri)

n

ax_ik-x_ij=b_i , i=1,.,n(2)

k=1

k I

x_ij 0 ,x_ij 0 (3)

Variabilele x_ij , i j si x_ij nu pot lua decat valori pozitive.

sau: Totalul cantitatilor Cantitatea aflata Consum net

ajunse in nodul i - in tranzit in nodul i = in nodul i

Costul transporturilor efectuate in cele n localitati este reprezentat prin urmatoarea functie ce trebuie minimizata

_{n m}

(min)f=aac_ijx_ij (4)

i=1 j=1

unde , c_ij=0 , i=1,.,n.

Ansamblul restrictiilor (1) si (2), conditia de nenegativitate (3) si functia obiectiv (4) constituie modelul matematic al problemei de transfer. Problema astfel definita este compatibila daca si numai daca totalul l al cantitatilor expediate din surse este egal cu totalul cantitatilor ajunse in destinatie, adica:

_nn

aa_i=ab_j=L (5)

i=1j=1

Restrictiile (1) si (2) ca si modul de formare al functiei obiectiv (4) pot fi citite usor pe liniile si coloanele tabelului 4.:

Tabelul4.

Reducerea problemei de transfer la problema clasica de transport.

Se constata ca in nici un nod cantitatea tranzitata nu poate depasi 'plafonul' l definit in (5).Pe aceasta baza introducem variabilele nenegative:

x_ii=L-x_ii , i=1,.,n

Substituind x_ii=L-x_ii (6)

in ecutia (1) si (2) problema de transfer se reduce la problema clasica de transport echilibrata:

n

ax_ik=L+a_i , i=1,n

k=1

n

ax_ik=L+b_i , i=1,n

k=1

x_ij 0 , i,j=1,n (7)

n m

(min)f=aac_ijx_ij

i=1j=1

Dupa rezolvarea problemei (7), relatia (6) ne permite sa punem in evidenta cantitatile aflate in tranzit in nodurile retelei.

Flux intr-o retea de transport

1.Problema cererii si a ofertei

Enunt: O anumita marfa este disponibila intr-un numar de locuri iIs si este ceruta in alte locuri jIt in cantitatile bj, jIt.

Admitem ca :

aa_i=ab_j=Q

iIs jIt

Intre surse si destinatii exista o retea de legatura, unele directe, altele indirecte. Pe unele transoane se poate circula in ambele sensuri, pe altele nu. Exista, de asemenea, limitari in ceea ce priveste cantitatile transportate de la un punct la altul. Intrebarea ce se pune este daca reteaua capacitata permite satisfacerea integrala a cererilor.

Problema cererii si a ofertei se reduce la o problema de flux maxim astfel:

se completeaza reteaua originala cu:

-un nod s si rutele orientate (s,i), iIs dotate cu capacitatile ai;

-un nod t si rutele orientate (j,t), jIt dotate cu capacitatile bj;

Un flux din reteaua extinsa de la s la t se poate asimila deplasarii unei cantitati de marfa din locul in care aceasta se afla disponibila spre locul unde este ceruta pentru consum. De aici rezulta ca valoarea oricarui flux de la s la t nu poate depasi valoarea Q. Construind fluxul maxim f* cererea in punctul de destinatie va fi acceptat integral numai daca v(f*)=Q.

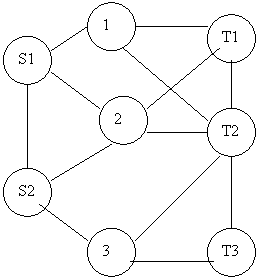
In prima figura de mai jos este vizualizata o retea de transport cu doua surse si trei destinatii, iar in cealalta apare reteaua extinsa.

9

17

15

13

6

a)reteaua initiala

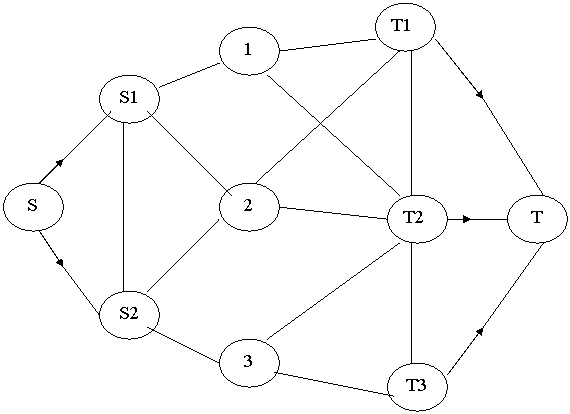
b)reteaua extinsa

figura 3.

In cazul in care in reteaua initiala totalul cantitatii de marfa ceruta difera de totalul cantitatii cerute, problema se va echilibra reducand sau majorand proportional cantitatile disponibile/cerute in nodurile sursa/destinatie.

Flux de volum maxim

Fie G=(X,T) o retea de transport finita, fara bucle cu un nod de intrare s si unul de iesire t. Fiecarui arc uIT al grafului ii este asociata o capacitate c(u)IZ.

Daca j(u) este fluxul asociat unui arc uIT, atunci, acesta, verifica relatia

0 j(u) c(u).

Fie j(u)IZ, marime intreaga.

Prin reteaua de transport se propaga un flux j j (u))_uIT care verifica proprietatea ca : « Suma fluxurilor pe arcele incidente spre interior, intr-un nod x este egala cu suma fluxurilor pe arcele incidente spre exterior, in acelasi nod x »,

aj(u)=aj(u).

uIU^-_x uIU _x

Proprietatea mai sus enuntata se numeste legea conservarii fluxului.

Fluxul reprezinta acea cantitate de materie ce trece prin arc (sau prin graf), materializata in vehicule, lichid,etc.

j_s reprezinta valoarea fluxului care circula printr-o retea de transport in nodul de intrare s.

j_t reprezinta valoarea fluxului care circula printr-o retea de transport in nodul de iesire t.

Din legea conservarii fluxului rezulta urmatoarea relatie :

j_s aj(u)=f aj(u)=j_t ,

uIU^-_tuIU _s

f-valoarea fluxului.

Daca pentru un arc uIT avem j(u)=c(u), arcul u este numit saturat.

Determinarea unui flux de volum maxim, ce trece prin reteaua de transport considerata, revine la determinarea unui flux care verifica conditiile de mai sus si pentru care valoarea f este maxima.

3.Algoritmul lui Ford-Foulkerson

Pentru determinarea unui flux de valoare maxima intr-o retea de transport data, se parcurge in general trei etape :

Etapa 1: Construirea unui flux compatibil

Fie intr-o ordine oarecare drumurile nesaturate care unesc intrarea s si iesirea t.Fie µ₁ un drum nesaturat de la s la t.Fluxul propagat de-a lungul acestui drum, este dat de urmatoarea relatie :

j_i =min[c(u)-j(u)]

^uI Vom obtine un nou flux care satureaza cel putin un arc, cu relatia :

j(u)+j_i ,cand uIµ_i

j(u)=

j(u) , cand uIµ_i

Daca reteaua de transport contine muchii, in identificarea drumurilor vom avea grija ca o ruta neorientata (muchie) sa nu fie folosita decat intr-un singur sens. In momentul identificarii unui drum se orienteaza si rutele. Pe fiecare arc se insumeaza fluxurile propagate.

Suma fluxurilor propagate de-a lungul drumurilor identificate este egala cu fluxul propagat in retea.

f aj_i

Etapa 2: Determinarea fluxului de valoare maxima

Pentru aceasta etapa se aplica urmatorul procedeu de marcare :

i)se marcheaza intrarea s cu [+] ;

ii)daca nodul i este marcat si (i,j)IT cu j(i,j)<c(i,j) atunci nodul i se marcheaza cu [+i];

iii)daca nodul j este marcat si (i,j)IT cu j(i,j)>0 atunci nodul i se marcheaza cu [-j] ;

vi)daca i este nod marcat si (i,j) este arc saturat atunci nodul j nu se marcheaza.

Daca iesirea t va fi marcata atunci exista un drum de la s la t.De-a lungul acestui drum notat µ_k se propaga un flux dat de relatia urmatoare :

j_k= min(min(c(u)-j(u)), min j(u)), j_k>0,

uIBuIC

B=multimea arcelor pe care se efectueaza marcaj de tip ii),

C=multimea arcelor pe care se efectueaza marcaj de tip iii).

Vom obtine un flux nou, imbunatatit, cu relatia

j(u)+j_k , cand uIB

j(u)= j(u)-j_k , cand uIC

j(u),in rest

Algoritmul se termina, in momentul in care nodul de iesire t al retelei nu mai poate fi marcat.

Fluxul de valoare maxima in reteaua de transport este egal cu suma fluxurilor propagate de-a lungul drumurilor si lanturilor care unesc nodul de intrare s cu nodul de iesire t.

Etapa 3: Determinarea taieturii de capacitate minima

Notam cu A multimea nodurilor nemarcate ale retelei, conform procedeului de marcare din etapa Multimea arcelor (i,j) cu iIA, jIA[incidente spre interior multimii A] notata cu UA se numeste taietura de capacitate minima in graf.

U A, granita intre nodurile marcate si nemarcate.Cu C(U A) vom nota capacitatea taieturii si se defineste ca fiind suma capacitatilor arcelor de :

C(U A)=ac(u)

^{uIU A}

In conformitate cu enuntul teoremei lui Ford-Foulkerson intr-o retea de transport data, fluxul de valoare maxima este egal cu capacitatea taieturii de valoare minima:

maxf j)=minC(U A)

j           s A

tIA

Arcele taieturii de capacitate minima fiind saturate inseamna ca pentru marirea fluxului propagat trebuie marita capacitatea unuia sau mai multor arce ale taieturii.

Varianta a algoritmului lui Ford-Foulkerson

Considerand un graf orientat, partial orientat sau neorientat, cu o intrare numita nodul sursa si o iesire numita nod terminal.

Se cere fluxul de valoare maxima intre nodul sursa si nodul terminal intr-o perioada de timp. Marimea fluxului este limitata pe fiecare muchie sau arc de capacitate care specifica disponibilul maxim in fiecare directie a arcului. Notam cu c_ij capacitatea arcului (i,j) in directia i j; c_ij reprezinta capacitatea aceluiasi arc (i,j) dar in cealalta directie j i. Daca un arc este orientat capacitatea in directia opusa este egala cu zero.

Fie C=(c_ij), matricea capacitatilor grafului.Inexistenta unui arc in graf, in matricea C se pune in evidenta prin '-'.

Consideram s ca fiind nodul sursa, iar t nodul terminal si n numarul nodurilor in graf.

Vom urma urmatorii pasi :

Pasul 1: -se determina un drum µ care conecteaza nodurile s si t, astfel ca, fluxul propagat sa fie mai mare ca zero pe fiecare arc al drumului. Daca nu exista un astfel de drum, se trece la pasul 3. Pasul 2: -se marcheaza cu c_ij capacitatile arcelor selectate in drumul µ in directia s t si cu c⁺_ij capacitatile arcelor aceluiasi drum in directia opusa t s.

Se defineste q=min>0.

Matricea C mai sus definita, se modifica astfel :

i) se scade q din toate elementele marcate c_ij ;

ii) se aduna q la toate elementele marcate c⁺_ij.

Cu aceasta noua matrice C se trece la pasul 1.

Conform modificarii i) cantitatea q propagata de la nodul s la nodul t trebuie redusa din capacitatile arcelor drumului m. Pe de alta parte ii) este introdusa pentru conservarea capacitatii arcelor. Descresterea capacitatii unui arc intr-o directie este echivalenta cu cresterea capacitatii aceluiasi arc in directie opusa.

Pasul 3: -in cadrul acestui pas se determina fluxul de valoare maxima in retea.

Daca C=(c_ij) este matricea initiala a capacitatilor vom nota cu C*=(c*_ij) ultima matrice in urma modificarilor. In C* nu se mai identifica nici un drum de la nodul s la nodul t.

Fluxul in arcele grafului se calculeaza folosind urmatoarea formula :

c_ij - c*_ij, daca c_ij>c*_ij

j_ij

0                , daca c_ij c*_ij

Fluxul maxim intre nodul sursa si nodul terminal este :

j₀ aj_si aj_jt

ij

j₀=suma marimilor q determinate in iteratiile (pasul 2) algoritmului.