|
|
|
Una dintre utilizarile importante ale coeficientului de corelatie este realizarea de predictii. Daca stim corelatia dintre doua variabile, putem sa prezicem valorile uneia dintre ele pe baza valorilor celeilalte. Este vorba despre o variabila predictor, si una variabila criteriu.
Asadar corelatia ar putea permite fundamentarea unei proceduri de "predictie" reciproca intre variabilele respective. Daca stim, de exemplu, ca doua variabile au o corelatie egala cu 1 (indiferent de semn) putem prezice orice valoare a unei variabile pe baza valorii celeilalte.
Formula de mai sus descrie modul de predictie in valori z pentru variabila Y, pornind de la valorile variabilei X, numita din acest motiv "predictor". Pentru ca valoarea lui Y din formula de mai sus este una "prezisa", se noteaza cu indicele "prim".
Sa ne imaginam ca am descoperit o corelatie perfecta (r=+1) intre scorul la un test de inteligenta verbala (X) si cel la un test de inteligenta abstracta (Y). Conform formulei, pentru o valoare zx=1.5 vom prezice o valoare identica pentru Y, zy'=1.5.
Din pacate corelatiile perfecte sunt rare sau de loc intalnite in realitate. Ca urmare, predictia suporta riscul unei erori. Pentru aceasta formula se modifica:
unde r este valoarea coeficientului de corelatie dintre cele doua variabile.
Conceptul de regresie a fost introdus de Francis Galton care, studiind relatia dintre inaltimea copiilor si a parintilor a observat ca parintii cu inaltimi excesive tind sa aiba copii cu inaltime mai mica decat a lor, adica mai aproape de medie decat a parintilor. Galton a denumit aceasta tendinta ca "regresie catre mediocritate". Dar pentru ca intra in calcul corelatia de tip liniar se vorbeste de "regresie liniara catre medie".
Reprezentarea grafica a regresiei
Imaginea alaturata reprezinta linia de regresie simpla in cazul unei corelatii perfecte pozitive (r=+1).
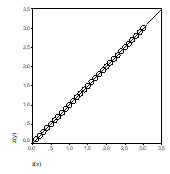Se poate observa ca distanta dintre
fiecare punct de intersectie si linie este nula, fapt ce ne
spune ca linia de regresie estimeaza perfect, fara erori,
modelul relatiei dintre cele doua variabile.
Atunci cand corelatia este diferita de 1, linia regresie este trasata pe o traiectorie de "aproximare" prin norul de puncte, astfel incat distanta dintre fiecare punct si linie sa fie cat mai mica posibil. In esenta, pentru a putea trasa dreapta de regresie a doua variabile, ne sunt necesare punctul de origine al acesteia si inclinarea, sau "panta". Odata aflate, putem trasa linia de regresie utilizand formula clasica a liniei drepte: Y=a+b*X, unde:
Y este valoarea prezisa a fiecarui punct de pe dreapta
a este originea dreptei, punctul in care linia de regresie intersecteaza ordonata (axa Oy).
b este panta liniei de regresie
X este valoarea predictor a variabilei Y
Intuitiv, linia de regresie poate fi vazuta ca o "medie" a norului de puncte, fiind trasata astfel incat distantele fata de punctele distributiei celor doua variabile sa fie similare de o parte si de alta a liniei.
Analiza reziduurilor
Linia de regresie se obtine, de fapt, prin cautarea unui traseu prin norul de puncte astfel incat distanta insumata dintre dreapta si punctele de deasupra sa fie egala cu distanta insumata fata de punctele de sub linie.
in cazul unei corelatii perfecte toate punctele de intersectie ale valorilor celor doua variabile se afla exact pe dreapta de regresie.
in cazul corelatiilor "imperfecte" distantele dintre puncte si dreapta de regresie exprima, de fapt, eroarea de estimare a asocierii dintre variabile. Distanta dintre pozitia reala a punctelor si cea estimata cu ajutorul liniei de regresie se numeste "valoare reziduala" si exprima, desigur, o eroare de estimare. .
Cu cit suma distantelor de la fiecare punct la linia de regresie este mai mare, cu atat eroarea de estimare este mai pronuntata. Cu cat vor fi mai apropiate punctele de intersectie de linia de regresie, cu atat mai putina eroare vom avea in predictie si, implicit, o corelatie mai mare. Invers, cu cat punctele de intersectie vor fi mai indepartate de linia de regresie, cu atat cu atat valoarea reziduala va fi mai mare iar corelatia va fi mai mica. La limita, pentru o corelatie egala cu 0, linia de regresie va avea o traiectorie orizontala, inclinarea ei fiind 0.
Utilitatea analizei de regresie
Analiza de regresie se utilizeaza in situatiile in care suntem interesati sa facem predictii asupra unei variabile, pe baza alteia obtinuta masurari anterioare. De exemplu, daca am efectuat o analiza de regresie intre coeficientul de inteligenta si performanta in munca pe un lot de subiecti, putem ulterior sa estimam nivelul performantei in munca a altor subiecti prin evaluarea inteligentei lor. Aceasta este procedura tipica pe care se bazeaza predictiile psihologice in contextul examenelor de selectie.
