INFERENTA STATISTICA

STRUCTURA MODULULUI

1. Proprietatile distributiei normale

2. Probleme de estimare

2.1. Semnificatia unei medii

2.2. Semnificatia frecventei

3. Sarcini sau probleme de comparatie

3.1. Semnificatia diferentei intre doua medii in cazul esantioanelor independente

3.2. Semnificatia diferentei intre doua medii in cazul esantioanelor perechi

Sumar

Bibliografie

Anexa.1.1 (distributia t)

Exercitii

Intrebari cu raspunsuri multiple

OBIECTIVELE MODULULUI

Dupa parcurgerea acestui modul studentul va cunoaste:

• proprietatile distributiei normale
• interpretarea semnificatiei mediilor si frecventelor
• rationamentul ipotezei nule
• modalitati de testare a ipotezei nule in cazul esantioanelor independente
• modalitati de testare a ipotezei nule in cazul esantioanelor perechi

1. PROPRIETATILE DISTRIBUTIEI NORMALE

Dupa cum s-a aratat, datele obtinute in cursul unei experiente, a unei observatii sistematice sau anchete, constituie un esantion pe care il consideram extras dintr-o "colectivitate" mai larga sau populatie. In final, extrapolam de la esantion la populatie, extindem concluziile asupra intregii colectivitati vizate prin cercetare.

Sa luam cateva exemple

1^o. Ne propunem sa determinam, pe baza unor metode precizate, volumul vocabularului la copiii de 5 ani. Prin enuntul ei, sarcina sau problema stabileste populatia pe care o avem in vedere: copiii de 5 ani. Ancheta noastra nu poate cuprinde in mod practic decat o subcolectivitate limitata, un esantion de populatie, in care un numar de N copii sunt alesi la intamplare. Inregistrarile facute pe acest lot stabilesc un volum al vocabularului sa zicem de 2024 de cuvinte. Un alt cercetator, propunandu-si aceeasi problema, ajunge la o cifra usor diferita, sa zicem 1936 de cuvinte. Repetand procedura, un al treilea cercetator gaseste 2000 de cuvinte.

2^o. Cerinte de ordin practic ne impun determinarea procentului tulburarilor de vorbire in clasele I-II, pentru a aproxima schema de organizare a retelei logopedice.

Determinarile efectuate pe cateva esantioane ne evidentiaza un procent de circa 12-13 %.

Se ridica intrebarea daca aceasta frecventa caracterizeaza populatia scolara din clasele mentionate.

3^o. Pentru organizarea retelei de invatamant special se ridica problema estimarii proportiei de deficienti mintali pentru palierul de varsta 6-7 ani. Determinarile arata un procent de circa 2%, daca se considera ca prag psihometric al debilitatii mintale IQ 70. Daca se fixeaza un prag mai sever, evident procentul va fi mai mare.

Aceste diferente de la un esantion la altul se datoresc hazardului si se numesc fluctuatii de esantionare. Situatia este identica si in alte conditii. Compozitia esantioanelor prezinta variatii, diferente intamplatoare in diferite studii pe aceeasi populatie. Daca vom lua de pilda, sase clase paralele de elevi dintr-o scoala si le vom supune aceleiasi probe vom constata diferente sau fluctuatii in rezultatele obtinute de la o clasa la alta. Este vorba despre fluctutii de esantionaj datorate factorilor aleatori. Un grup natural intact, luat in compozitia sa data, constituie un esantion la intamplare, daca nu au intervenit factori de selectie controlati de noi.

Prelucrarea statistica, asa cum am vazut, reduce datele brute la cateva valori caracteristice: frecvente sau procente, medii, abateri standard etc. Se pune intrebarea: in ce masura datele obtinute sunt relevante pentru populatie. Aceasta operatie se numeste inferenta statistica.

Datele obtinute asupra esantionului se apropie de indicii adevarati ai populatiei, aceasta apropiere sau aproximatie fiind cu atat mai mare cu cat volumul esantionului N este mai mare.

Practic, nu reusim sa determinam exact indicii caracteristici ai populatiei. Indicii esantionului constituie estimari ale parametrilor populatiei. In exemplul ales mai sus, volumul mediu m - stabilit pe baza studierii grupului de copii - reprezinta o estimare a mediei adevarate a colectivitatii generale. Intrucat nu se pot cerceta toti copiii de 5 ani ne bazam in afirmatiile noastre pe datele asupra esantionului cercetat. Luand ca baza indicii esantionului, extrapolandu-i deci la populatie, comitem o anumita eroare, a carei valoare probabila trebuie sa fie, evident, cat mai mica.

In felul acesta, in legatura cu indicii stabiliti asupra esantionului - medii sau frecvente - se pune problema erorii probabile pe care o comitem bazandu-ne pe ei in extrapolarea la populatie.

Rationamentul se intemeiaza pe proprietatile distributiei normale, schitate deja in capitolul precedent in legatura cu semnificatia abaterii standard. In psihologie, ca si in alte domenii, modelul distributiei normale este un model privilegiat, pentru ca il regasim in numeroase situatii.

S-a stabilit ca ±2σ, mai exact ±1,96σ, in raport cu media acopera 95% din rezultate (elemente). Cu alte cuvinte, 95% din elemente cad in intervalul m ± 1,96σ, iar 5% cad in afara acestui interval. Procentul de 5% se compune din 2,5%, respectiv 2,5% de o parte si de alta a mediei spre extremitatile distributiei.De asemena, s-a stabilit ca 99% din rezultate (elemente) sunt cuprinse in intervalul m ± 2,58σ , in timp ce 1% (0,5% + 0,5%) din elemente sunt exterioare acestui interval. (Fig. 1.).

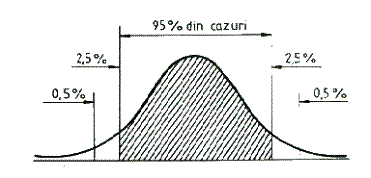
Figura 1. Proprietatile distributiei normale

Pentru a evita o anumita variabilitate a situatiilor se introduce o distributie - standard. Variabila bruta x se inlocuieste cu variabila normata z pe baza formulei de transformare deja amintite:

prin care se imparte fiecare abatere de la medie (x - m) cu abaterea standard σ. Gratie transformarii amintite, orice distributie normala, are media egala cu zero si varianta egala cu 1. Pentru aceasta ultima distributie s-a intocmit un tabel, care permite sa avem proportia de elemente pentru care variabila este exterioara unui interval oarecare centrat pe medie.

Este vorba de tabelul legii normale reduse , care ne permite sa vorbim in cele din urma in limbajul sanselor, al probabilitatilor. Variabila redusa | z | prezinta de regula valori intre 0 si 3,00 (cu doua zecimale). Figura 2 reda un exemplu pentru | z | = 1,00. Variabila initiala x este inlocuita cu variabila standardizata z, avand m = 0. Din punctele z, respectiv - z, ridicam ordonatele corespunzatoare, care indica punctele de inflexiune ale curbei si hasuram spre cele doua extremitati suprafata exterioara benzii cuprinse intre cele doua ordonate (Fig. 2).

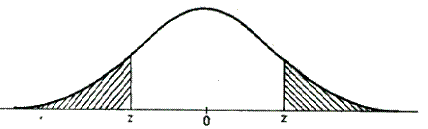
Fig. 2.

Pentru | z | = 1,00 corespunde o valoare de 0,317, ceea ce inseamna ca pentru un element extras la intamplare din multime exista 317 sanse dintr-o mie ca acesta sa cada in una din suprafetele hasurate - intr-o parte sau alta- deci sa-i corespunda o valoare | z | >1,00. Retinem in continuare doua repere: pentru | z | =1,96 corespunde 0,05 , iar pentru

| z |= 2,58 , valoarea 0,01. Cu alte cuvinte, exista 5 sanse din 100 ca unui element considerat la intamplare din multime sa-i corespunda o valoare | z | > 1,96, dupa cum exista o sansa din 100 ca | z | sa fie mai mare decat 2,58. De aceste doua repere, frecvent utilizate, se leaga deci sanse sau probabilitati precizate: 5%, respectiv 1%.

Rezumand: intr-o distributie normala standard avem 95% din valorile z cuprinse intre -1,96 si + 1,96; de asemenea avem 99% din valorile z cuprinse intre -2,58 si +2,58.

De aici se poate face pasul spre o distributie normala oarecare avand media m si abaterea standard σ. Intrucat variabila standardizata z s-a obtinut - plecand de la variabila initiala x - gratie formulei:

reiese ca: a spune ca z este cuprins intre -1,96 si +1,96 inseamna a spune ca

-1,96 < (x-m)/σ < 1,96

sau

(m - 1,96σ) < x < (m + 1,96σ),

ceea ce s-a enuntat la inceput.

Cu alte cuvinte, exista 95% din valorile x interioare intervalului :

[m - 1,96σ; m +1,96σ],

dupa cum exista 99% din valorile x interioare intervalului:

[m - 2,58σ; m + 2,58σ].

Afirmatiile facute anterior au devenit astfel propozitii motivate.

2. PROBLEME DE ESTIMARE

Asa cum s-a aratat, marcam indicii esantionului cu o bara asazata deasupra , ,, iar parametrii populatiei ii notam in mod obisnuit: m, f, σ. Pornind de la indicii esantionului stabilim cu o anumita probabilitate valoarea parametrilor. In mod obisnuit nu putem determina exact valoarea parametrului, ci stabilim un interval in care se gaseste cu certitudine practica parametrul respectiv. Cu cat acest interval este mai mic, cu atat informatia noastra asupra adevaratei valori in populatie este mai precisa . Se cere deci o concentrare a masei de probabilitate intr-o regiune restransa. Intervalul mentionat se numeste interval de incredere.

2.1. Semnificatia unei medii

Semnificatia unei medii depinde pe de o parte de volumul esantionului studiat (N), iar pe de alta parte, de variabilitatea populatiei (σ) din care s-a extras grupul dat. Cu cat volumul datelor creste, cu atat media devine mai stabila si deci mai reprezentativa.

S-a numit eroarea standard a mediei cantitatea σ/ care se noteaza cu E. Aceasta ne ofera un etalon pentru a evalua eroarea ce o comitem luand drept baza media esantionului in locul mediei adevarate m a colectivitatii generale (pe care practic nu reusim de cele mai multe ori sa o determinam).

In relatia de mai sus σ reprezinta abaterea standard a colectivitatii generale, care ramane aproape intotdeauna necunoscuta, fiind inlocuita in calcule cu determinata pe baza datelor esantionului (cand N este destul de mare).

Reluand tabelul din tabelul 3.4, avem:

N=51; ; ;

Facand inlocuirile:

In mod curent nu ne putem astepta sa determinam valori punctuale pentru parametrii populatiei. In acest sens se stabilesc intervale. Pe baza erorii standard a mediei E se stabilesc limitele intre care se gaseste, cu o probabilitate data adevarata valoare m a colectivitatii generale. Aceste limite se numesc limite de incredere, iar intervalul delimitat de ele este intervalul de incredere. Intrucat mediile prezinta distributie normala, se stabilesc drept limite de siguranta : -1,96E si +1,96E.

In exemplul mentionat vom avea: L₁ = 13,17 - (1,96 x 0,66) si L₂ = 13,17 + (1,96 x 0,66). Efectuand inmultirile obtinem: 13,17 +/- 1,29, adica 11,88 si 14,46. Acestea sunt limitele intre care se gaseste aproape sigur (cu o probabilitate de 95%) adevarata medie m a colectivitatii generale.Afirmand ca media adevarata se va gasi intre 11,88 si 14,46 riscam totusi sa gresim in 5% din cazuri.

Se obisnuieste sa se noteze si riscul pe care ni-l asumam de a gresi facand o asertiume sau alta. Aceasta a capatat denumirea de prag sau nivel de semnificatie. Astfel, intervalul (-1,96E; +1,96E) se numeste interval de incredere la pragul de p = 0,05, ceea ce inseamna ca in 5% din cazuri adevarata medie se afla in afara intervalului ales. In practica, se ia adeseori pragul p = 0,01, ceea ce indica riscul de a gresi in 1% din cazuri. Limitele de incredere vor fi atunci L₁=-2,58E si L₂=+2,58E.

2.2. Semnificatia frecventei

Transpunand notiunile prezentate anterior, putem spune ca eroarea - tip a frecventei este:

si ca limitele de incredere, la pragul de p = 0,05vor fi:

.

Practic, N fiind mai mare (>100), vom comite o eroare foarte mica inlocuind in calculul limitelor de incredere pe p prin f , si pe q prin 1- f. Dupa inlocuire vom avea:

Exemplu (dupa Faverge)

Sa consideram un exemplu.

Intr-o statistica a erorilor de la casierie s-au observat 134 de erori in plus si 289 de erori in minus. Frecventa f a erorilor in plus este:

(423 = 134 + 289).

Vom avea:

La pragul de semnificatie de p = 0,05, limitele de incredere se obtin calculand:

1,96 x 0,020 = 0,0

Ele sunt:

0,32 + 0,04 = 0,36,

0,32 - 0,04 = 0,28.

Cu alte cuvinte, admitand ca esantionul nostru face parte din cele 95% pentru care parametrii se situeaza in intervalul de incredere, putem afirma ca procentajul erorilor in plus va fi cuprins intre 36% si 28%.

3. SARCINI SAU PROBLEME DE COMPARATIE

In chip frecvent intervin in cercetarile psihologice probleme de comparatie. Astfel, se compara intre ele mediile obtinute intr-o experienta si se pune intrebarea daca diferentele constatate sunt semnificative sau nu, se pot extinde la populatie sau nu.

Exemplu (dupa I. Radu):

Intr-o experianta de instruire programata au fost cuprinse doua clase paralele. La probele de control date in post- test s-a constatat la clasa experimentala - cu un efectiv de 33 elevi - o medie a notelor de 7,7, iar in clasa de control (N = 34), media la aceleasi teste a fost de 6,7. Diferenta dintre medii este 1,00. Se pune intrebarea daca aceasta diferenta este semnificativa, daca putem extrapola la populatie, ceea ce ne indica daca metoda de instruire incercata este mai buna decat cele curente.

Rezultatele unei investigatii pot sa apara exprimate si sub forma de frecvente sau proportii. In exemplul citat mai sus rezultatele experimentului ar putea fi exprimate si in frecvente, indicand proportiile consemnate de raspunsuri corecte si de raspunsuri gresite. Si in cazul acesta se pune intrebarea daca diferentele constatate sunt semnificative sau nu. Raspunsul la intrebarea pusa s-ar putea obtine repetand experienta. Daca rezultatele se mentin statornice vom putea conchide asupra semnificatiei lor. Cum experientele nu se pot repeta indefinit - procedeu de altfel neeconomic - s-a conturat un mecanism logic prin care se infirma ipoteza hazardului, notata H₀.

In conditiile experientei obisnuite ne-am putea multumi cu diferente intre medii de 0,5 sau 0,7 ori 0,9 s.a.m.d., dupa cum diferente de 5%, 7% etc intre frecvente ar parea doveditoare.

Experimentul stiintific nu poate face extrapolari la populatie bazate doar pe simpla evaluare intuitiva. Intrebarea este: de la ce nivel (0,5 sau 0,7, respectiv 5%; 7%;) diferentele pot fi considerate semnificative?

In orice experienta studiem procesul dat in anumite conditii, intr-un anumit context: la lectie, la joc, in activitatile practice, in conditii de laborator etc. Trebuie sa admitem ca, intr-un fel sau altul, intamplarea poate interveni in desfasurarea fenomenului cercetat prin conditii neasteptate, prin compozitia grupului, prin deosebiri in personalitatea profesorului etc. Datele obtinute sunt afectate in felul acesta de un element aleator (intamplator). In consecinta, alaturi de ipoteza specifica (H_s), ce sta la baza experientei respective si care este o ipoteza psihologica sau pedagogica se poate formula si o alta ipoteza care sa atribuie numai intamplarii tendintele sau diferentele constatate. Aceasta din urma este 'ipoteza intaplarii'sau ipoteza nula (H₀) si se enunta pentru toate cazurile in aceiasi termeni. De notat ca atat ipoteza nula (H₀) cat si ipoteza alternativa (H_s) se refera la populatie, nu la esantioane ca atare.

Preocupat sa dovedeasca in mod temeinic justetea ipotezei specifice, cercetatorul va admite in mod provizoriu -in rationamentul sau - ipoteza nula si va determina sansele (probabilitatea) ca diferentele obtinute in experiment sa aiba loc numai pe baza ' legilor intamplarii' (care sunt legi de probabilitate bine studiate). Stim ca probabilitatea ia valori intre 0 si 1, iar transcrisa in procente - intre 0 si 100%.

Daca probabilitatea obtinerii diferentei date, in baza ipotezei nule, este foarte mica (de pilda, mai mica decat 0,05 ceea ce se scrie p < 0,05), atunci respingem ipoteza hazardului si aratam toata increderea ipotezei specifice. Daca insa, probabilitatea determinata in lumina ipotezei nule este mai mare (de pilda, p > 0,10 putand merge pana la 1), atunci nu ne putem asuma riscul respingerii ipotezei nule si vom considera diferentele efectiv obtinute ca fiind inca nesemnificative.

Prin urmare se accepta ca semnificative acele rezultate care au sansele de a se produce prin simpla intamplare numai intr-un numar mic de cazuri: sub 5% din cazuri, uneori sub 10%. Sansele de a obtine rezultatele respective prin simplul joc al factorilor aleatori se afla in acest caz sub 10%, respectiv 5% ( ceea ce se scrie p < 0,10 respectiv p < 0,05). Inseamna ca, acceptand rezultatele unei experiente drept proba justetei ipotezei specifice, ne asumam totodata riscul de a gresi in mai putin de 10%, respectiv 5% din cazuri. Fiecarei asertiuni i se asociaza astfel un prag de semnificatie, care indica riscul de a gresi pe care ni-l asumam.

Rezumand: mecanismul logic al ipotezei nule permite infimarea ipotezei hazardului si acceptarea in consecinta a ipotezei alternative (H_s). Ipoteza nula si ipoteza alternativa sunt contradictorii; a respinge ipoteza nula inseamna a accepta ipoteza specifica. Daca plasam pe o axa probabilitatile amintite vom avea situatia din figura 3.

10,05 0,01 p

|----- ----- ---------- . . . ----- ----- -------|----- ----- --------|----- ----- -------->

H₀ nu se considera infirmata | H₀ se considera infirmata

si se suspenda decizia si se accepta H_s

limita semnificativitatii

Fig. 3

Respingand ipoteza nula si accepand existenta unui efect al variabilei independente - ceea ce sustine H_s - ne asumam un risc de a gresi destul de mic: 5% respectiv 1%. Masurarea acestui risc, notata cu α, constituie pragul de semnificatie, care insoteste fiecare asertiune.

Se poate intapla ca ipoteza nula sa nu fie infirmata, z cal fiind mai mic decat 1,96 (deci p > 0,05). In cazul acesta nu se conchide ca H₀ ar fi validata, ci, pur si simplu, ca nu se poate decide; intervine o zona de suspendare a judecatii. Valoarea | z | care separa cele doua zone - zona de respingere a ipotezei nule si zona de suspendare a judecatii - se numeste valoare critica. Ea corespunde valorii z cal avand o probanbilitate asociata egala cu α. Riscul de a gresi α se poate lua 10%, 5%, 1%. Traditia a acreditat pragul de p≤ 0,05 sau p≤ 0, 01. In functie de cerintele cercetarii se alege pragul indicat.

De notat ca ipoteza nula nu poate fi niciodata acceptata; a nu se respinge H₀ nu echivaleaza cu acceptarea ei. In schimb, ipoteza specifica nu poate fi niciodata respinsa. Fiind o ipoteza statistica imprecisa nu se poate calcula distributia de esantionaj sub ipoteza alternativa (Abdi, 1987).

Valorile cririce ale criteriului z, t, s.a. au fost calculate pentru diferite praguri a fiind prezentate sub forma de tabele ce urmeaza doar a fi consultate. Regula de decizie este precizata:

- daca criteriul z, calculat pe esantionul experimental este mai mare sau egal cu valoarea critica (z critic), probabilitatea sa asociata este mai mica sau egala cu pragul α (se decide respingerea H₀);

- daca criteriul z cal, calculat pe esantionul experimental, este mai mic decat valoarea critica (z critic), probabilitatea asociata este mai mare decat pragul α. In consecinta intervine suspendarea judecatii: nu se va respinge nici accepta H₀. In sens strict, se va decide de a nu se decide (Abdi, 1987).

In probleme de comparatie statistica urmeaza sa se faca distictia intre esantioane independente si esantioane perechi.

O clasa de elevi, spre exemplu, poate fi considerata practic ca un esantion la intamplare extras dintr-o colectivitate mai larga. Daca se considera o alta clasa, paralela, in vederea unei experiente determinate, atunci alegerea poate fi facuta in doua feluri. Se pot alege in mod independent cele doua esantioane: faptul ca un element sau altul din primul esantion a fost ales nu are nici o influenta asupra alegerii elementelor din esantionul al doilea. Compozitia celor doua grupe nu este reglementata pe baza unei probe prealabile; cele doua clase sunt considerate in compozitia lor stabilita prin ' legile intamplarii'. In acest caz este vorba despre esantioane independente.

Se poate proceda si altfel. Se pot constitui esantioane perechi. In cazul acesta, fiecare element dintr-un esantion corespunde unui element dintr-un alt esantion (formeaza o pereche cu el). De exemplu, pentru a compara doua metode de instruire se constituie doua grupe cu acelasi numar de elevi, astfel ca fiecarui elev dintr-o grupa sa-i corespunda un elev din cealalta grupa, avand acelasi nivel de cunostinte, eventual acelasi C.I. In felul acesta, compozitia grupelor este precizata pe baza unei probe anterioare, in virtutea careia elementele celor doua esantioane nu se determina la intamplare. Fiecare individ dintr-o grupa are 'corespondent" in grupa a doua, avand aceeasi nota (sau acelasi nivel) in proba preliminara. Situatia este identica si in cazul cand acelasi grup de subiecti este supus de doua ori la probe diferite (de exemplu, inainte si dupa actiunea unui anumit factor experimental). Se obtin atunci doua grupe de masurari efectuate pe aceiasi subiecti, care constituie perechi.

Prin urmare putem alege grupele de studiu in mod independent si atunci este vorba de o alegere la intamplare a elementelor; sau putem asocia intr-un anumit fel - pe baza unui criteriu precis - elementele celor doua esantioane, doua cate doua, si atunci compozitia lor este determinata de regula in virtutea unei probe prealabile: test de inteligenta, test de cunostinte etc.

3.1. Semnificatia diferentei intre doua medii in cazul

esantioanelor independente

Probele de semnificatie difera in functie de doua situatii:

●cand numarul de masuratori (N) in fiecare esantion este destul de mare (mai mare ca 30);

●cand numarul de masurari sau volumul esantionului este mai mic dacat 30.

In experimentele cu caracter instructiv de la care am pornit N₁= 33 si N₂ = 34, deci ne aflam in prima situatie.

Pentru a vedea daca cele doua medii constatate difera semnificativ, facem rationamentul care urmeaza.

Admitem pentru moment ipoteza nula si stabilim care este sansa de a fi verificata. Cu alte cuvinte presupunem ca diferenta intre cele doua medii si se datoreste intamplarii si ca nu exista diferente reale intre esantioanele considerate. In limbaj statistic inseamna ca cele doua grupe constituie esantioane extrase la intamplare din aceeasi populatie.

Pentru a testa ipoteza nula se utilizeaza criteriul sau raportul:

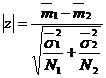
in care notatiile sunt deja cunoscute.

Calculand valoarea raportului de mai sus, notat cu | z |, ne vom referi la proprietatile curbei normale schitand valorile calculate (z cal) in raport cu valorile critice (1,96 si 2,58). Daca valoarea ce va corespunde indicelui z cal este mai mare decat 1,96, atunci diferenta intre cele doua medii este semnificativa la pragul de p < 0,05, iar daca z cal > 2,58, atunci diferenta este semnificativa la pragul de p < 0,01. Bineinteles, daca vom avea z cal < 1,96, atunci ipoteza nula nu va fi infirmata, iar diferenta obtinuta in cadrul experientei nu va fi considerata concludenta pentru a proba justetea ipotezei specifice (vom suspenda decizia).

In exemplul considerat trebuie sa cunoastem cu privire la fiecare grup , N si .

Utilizand formula stabilita obtinem:

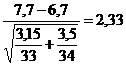
Raportul gasit este mai are decat 1,96 si mai mic decat 2,58, deci p < 0,05. Facand un calcul de interpolare se afla p = 0,02; deci diferenta este net semnificativa, ipoteza nula fiind infirmata.

Cand volumul datelor obtinute in fiecare esantion este mai mic (numarul de masurari este mai mic decat 30) se utilizeaza un procedeu intrucatva diferit.

Ipoteza nula se enunta la fel: presupunem ca cele doua grupe de date sunt doua esantioane intamplatoare ce provin din aceesi colectivitate generala. Verificam apoi sansa acestei ipoteze pe baza criteriului t:

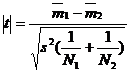
Pentru a obtine o estimare a dispersiei colectivitatii - care este notata in formula cu s² - se combina datele celor doua esantioane:

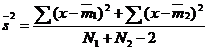
Formulele de la numarator ne sunt cunoscute de la calcularea dispersiei (sumei de patrate referitoare la cele doua grupe), iar N₁ si N₂ sunt efectivele celor doua esantioane.

Exista un tabel special (intocmit de Student) in care figureaza probabilitatile raportului | t | corespunzator numarului 'gradelor de libertate' care depinde de volumul esantioanelor (vezi Anexa 1.1.). In cazul nostru numarul acesta - notat n - este:

n = N₁ + N₂ - 2.

Sa luam un exemplu.

In procesul invatarii esalonarea repetitiilor este mai productiva decat concentrarea lor. Intr-o experienta se ia cate o grupa formata fiecare din cate 10 subiecti si se experimenteaza in cele doua situatii prevazute: repetitii esalonate sau concentrate in timp. Inca din prima perioada subiectii manifesta o diferenta. Vrem sa stim daca ea este semnificativa (dupa P. Oleron).

Datele consemnate de autor sunt:

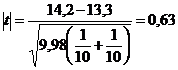
| t | fiind calculat, ne referim la tabelul distributiei | t | intocmit de Student. Acest tabel prezinta o coloana n sau v, care corespunde gradelor de libertate. In tabelul de mai sus n = 10 +10 - 2 = 18. Cautam in coloana n pe 18. Dupa ce l-am fixat, mergem pe randul respectiv si cautam valoarea lui | t | la pragul de 0,05 si 0,01 (probabilitatea o citim in prima linie de sus a tabelului unde gasim de la dreapta spre stanga: 0,01; 0,02; 0,05; 0,10). In cazul nostru tabelul indica 2,10 pentru | t | la pragul de 0,05 respectiv 2,88 la oragul de 0,01. Valoarea calculata in exemplul ales este 0,63, deci este mult mai mica decat 2,10 careia ii corespunde p = 0,05. Putem spune atunci ca pentru | t | = 0,63 avem p > 0,05. si astfel ipoteza nula nu este infirmata. Consideram diferenta dintre medii ca nesemnificativa, mai exact suspendam decizia.

In general, daca valoarea gasita prin calcul este mai mica decat valoarea | t | indicata in tabel la pragul p = 0,05, atunci consideram ca ipoteza nula nu este infirmata, iar diferentele obtinute in experienta ca nesemnificative. Daca valoarea calculata de noi este mai mare decat valoarea | t | la pragul 0,05, dar mai mica dacat valoarea lui | t | la pragul de 0,01, vom spune ca diferenta este semnificativa la pragul de 0.05. In sfarsit, daca valoarea gasita de noi este mai mare decat valoarea | t | indicata in tabel pentru

p = 0,01, atunci vom spune ca diferenta este semnificativa la pragul de 0,01.

Observam ca respingerea ipotezei nule se face considerand un prag de semnificatie ales in prealabil (cel mai riguros este p = 0,01). De retinut este faptul ca ipoteza nula nu se considera niciodata demonstrata; ea poate fi doar infirmata. Efectul admiterii sau respingerii ipotezei nule se rasfrange asupra ipotezei specifice. Neinfirmarea ipotezei nule pune sub semnul intrebarii ipoteza specifica, infirmarea ipotezei nule consolideaza foarte mult ipoteza specifica. Cele doua ipoteze H₀ si H_s sunt, cum s-a spus, contradictorii.

3.2. Semnificatia diferentei intre doua medii in cazul

esantioanelor perechi

Cand elementele celor doua esantioane sunt asociate intr-un anumit mod doua cate doua (de exemplu, rezultatele inregistrate inainte si dupa actiunea unui factor experimental), procedeul cel mai simplu consta in a rationa asupra diferentelor pe care le prezinta fiecare pereche de date asociate, corelate.

Sa notam cu x rezultatele din primul grup de masurari (esantion) si cu x' valorile asociate din esantionul al doilea. Diferenta corespunzatoare fiecarei perechi de note x - x' o insemnam cu d. Se obtin astfel patru coloane.

Exemplu

Cu o grupa de 10 elevi s-a incercat la geografie, in decursul trimestrului II al anului scolar, o metoda noua de invatare individuala, pe baza unor intrebari de control fixate pe cartonase. S-au inregistrat notele elevilor la geografie la inceputul experientei, adica la sfarsitul trimestrului I si apoi la incheierea trimestrului II. Vrem sa stim daca metoda respectiva aduce o imbunatatire semnificativa a situatiei scolare.

Pentru a determina acest lucru intocmim un tabel in care vom inscrie subiectii, rezultatele obtinute in cele doua situatii si vom calcula diferentele dintre ele (Tab.1.).

Se observa din tabel ca avem diferente nule, pozitive si negative.

Formulam ipoteza nula, adica atribuim numai intamplarii diferentele constatate, Daca s-ar datora numai intamplarii, aceste diferente ar fluctua in jurul lui 0 intr-un sens sau altul, iar media lor ar fi egala cu zero m_d= 0 (cu m_d am notat media diferentelor).

Tabelul 1

Vom insuma algebric coloana d (tinand deci seama de semne) si vom afla

∑d = T. Apoi, facand raportul T/N, vom afla media diferentelor m_d.

In exemplul ales, m_d = T/N = 0,09, deci m_d difera de zero; nu stim daca diferenta aceasta este suficient de mare pentru a putea fi considerata semnificativa sau nu.

Se utilizeaza criteriul:

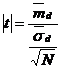
in care cunoastem si N, dar nu cunoastem (abaterea standard a diferentelor).

Tratam diferentele asa cum am considerat inainte datele brute.

Calculam mai intai dispersia diferentelor:

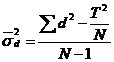
si

In exemplul ales adaugam in tabel o coloana d^2, pe care insumand-o obtinem Σd²=27.

Facand inlocuirile:

de unde

Deci

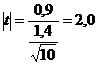
Cautam in Anexa 1.1. | t | tinand seama de faptul ca in acest caz numarul gradelor de libertate este N - 1 (si nu N₁+N₂- 2, ca in primul caz).

In exemplul de mai sus, N - 1 = 9. Cautand in tabel gasim pentu 9 grade de libertae,la pragul de p = 0,05 cifra 2,26. Valoarea calculata de noi este inferioara acestei cifre. Inseamna ca nu s-a demnostrat falsitatea ipotezei nule si, in felul acesta nu se poate spune ca rezultatele experientei sunt semnificative.

Cand N este destul de mare (>60) putem raporta valoarea gasita prin calcul la valorile z (1,96 si 2,58) fara sa mai facem apel la Tabelul lui Student.

Trebuie reamintit in incheiere ca atat raportul | z | cat si criteriul | t | presupun drept conditie aspectul normal al distributiilor supuse comparatiei.

Sumar

In cercetarea psihologica modelul consacrat este cel al investigarii la nivelul esantioanelor urmat de extrapolarea la nivelul populatiei, proces denumit inferenta. In cadrul inferentei statistice se disting doua tipuri de probleme: probleme de estimare, respectiv probleme de comparatie. Problemele de estimare, permit pe baza unui indice obtinut la nivelul esantionului estimarea cu o anumita probabilitate a intervalului in care se afla parametrul pentru populatie. In problemele de comparatie pe baza unor teste de semnificatie adaptate situatiei concrete se determina probabilitatea ipotezei nule (pragul de semnificatie). In cazul esantioanelor independente se folosesc doua teste in functie de volumul esantionului; pentru esantioane cu efective mai mari de 30 de subiecti se utilizeaza testul z, iar pentru esantioane cu un volum sub 30 de subiecti testul t. In cazul esantioanelor perechi se foloseste testul t.

Bibliografie

Abdi H. (1987). Introduction ou traitemant statistique des données expérimentale, Grenoble:

Presses Universitaire de Grenoble.

Faverge, J.M. (1965). Méthodes statistiques en psychologie appliquée. t.III, Paris, P.U.F.

Jaccard J & Becker, M. (1997). Statistics for the behavioral sciences (third edition), Brooks, Cole Publishing Company, Pacific Grove.

Rouanet, H., Le Roux, B., Best, C. (1987). Statistique en sciences humaines: procedures naturelles, Paris, Bordas.

Spence, J., Underwood, B.J., Duncan, C.P., Cotton, J.W. (1968). Elementary statistics, New York, Appleton

ANEXA 1.1.

Distributia t

EXERCITII

1. Precizati si explicati care este rolul inferentei statistice in prelucrarea datelor unei cercetari de psihologie experimentala.

2. In ce conditii intreaga colectivitate a universitatii in care invatati poate fi considerata o populatie? In ce conditii colectivitatea universitatii poate fi considerata un esantion? In cazul in care colectivitatea universitatii este folosita ca si esantion, cum este realizata selectia ? Se poate vorbi de o selectie randomizata? De ce?

3. Avand urmatoarele ipoteze specifice, formulati pentru fiecare ipoteza nula corespunzatoare.

1.      Exista o diferenta intre baieti si fete in ceea ce priveste abilitatile de invatare si domeniile de studiu pentru care prezinta interes: baietii preferand stiintele exacte, iar fetele stiintele sociale.

2.      Persoanele cu un stil de invatare vizual retin mai multe informatii din grafice decat persoanele cu un stil de invatare verbal.

3.      Un program regulat de exercitii duce la imbunatatirea performantelor scolare.

Ce rol are formularea si testarea ipotezei nule in desfasurarea unui experiment prin care se testeaza ipotezele specifice formulate?

INTREBARI CU RASPUNSURI MULTIPLE

1.Pornind de la indicii unui esantion se pot:

a)      calcula parametrii populatiei

b)      estima parametrii populatiei

c)      determina intervalul in care se gasesc parametrii populatiei

d)      determina probabilitatea cu care parametrii populatiei se incadreaza intr-un anumit interval

e)      determina valoarea parametrilor populatiei

R. b,c,d,

2. Pe baza unui test de semnificatie statistica s-a determinat o probabilitate a ipotezei nule H₀ de 0,01. Ce probabilitate va avea ipoteza specifica H_S in acest caz?

a)      99%

b)      95%

c)      1%

d)      toate raspunsurile sunt corecte

e)      toate celelalte raspunsuri sunt gresite

R. e

3. Cand probabilitatea ipotezei nule (H₀ ) este mai mare de 5%:

a)      putem accepta ipoteza specifica

b)      putem accepta ipoteza nula

c)      respingem ipoteza specifica

d)      respingem ipoteza nula

e)      se suspenda decizia

R. e