CARACTERISTICI ALE ESTIMATORILOR
Un estimator
trebuie sa satisfaca doua conditii: sa fie
nedistorsionat si relativ eficient. Se spune ca un estimator este nedistorsionat,
daca media aritmetica a distributiei sale de esantionare
este egala cu media aritmetica a populatiei de
referinta. Conform teoremei limitei centrale, mediile aritmetice ale
esantioanelor satisfac aceasta conditie: media aritmetica a
distributiei de esantionare a mediilor aritmetice,  , este egala cu media aritmetica a populatiei,
μ. Statisticienii au demonstrat ca si proportiile
esantioanelor, p, sunt nedistorsionate, intrucat media
aritmetica a distributiei de esantionare a proportiilor
pentru esantioane, μp, este egala cu
proportia populatiei, P. Prin contrast, un estimator este distorsionat,
daca media aritmetica a distributiei sale de esantionare
este diferita de media aritmetica a populatiei. De pilda,
abaterea standard a unui esantion este un estimator distorsionat al
abaterii standard a populatiei: de regula, dispersia unui
esantion este mai mica decat cea a populatiei de
referinta, astfel ca s tinde sa subestimeze pe σ.
Dupa cum am mentionat in capitolul 3, aceasta distorsiune poate
fi corectata.
, este egala cu media aritmetica a populatiei,
μ. Statisticienii au demonstrat ca si proportiile
esantioanelor, p, sunt nedistorsionate, intrucat media
aritmetica a distributiei de esantionare a proportiilor
pentru esantioane, μp, este egala cu
proportia populatiei, P. Prin contrast, un estimator este distorsionat,
daca media aritmetica a distributiei sale de esantionare
este diferita de media aritmetica a populatiei. De pilda,
abaterea standard a unui esantion este un estimator distorsionat al
abaterii standard a populatiei: de regula, dispersia unui
esantion este mai mica decat cea a populatiei de
referinta, astfel ca s tinde sa subestimeze pe σ.
Dupa cum am mentionat in capitolul 3, aceasta distorsiune poate
fi corectata.
Un estimator
nedistorsionat permite, intre altele, determinarea probabilitatii ca
o marime statistica a unui esantion sa se afle la o
anumita distanta fata de parametrul corespunzator
pe care incercam sa-l estimam. Pentru ilustrare, sa
presupunem ca ne intereseaza venitul mediu al unei populatii.
Pentru aceasta, alcatuim un esantion aleatoriu cu n = 500
si calculam media aritmetica pentru acest esantion. Sa
presupunem ca am gasit  . Dupa cum am aratat, variabila venit
prezinta o distributie asimetrica. Cu toate acestea, conform
teoremei limitei centrale, distributia de esantionare a
. Dupa cum am aratat, variabila venit
prezinta o distributie asimetrica. Cu toate acestea, conform
teoremei limitei centrale, distributia de esantionare a 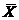 pentru esantioane mari (n 100) aproximeaza normalitatea, avand media
aritmetica,
pentru esantioane mari (n 100) aproximeaza normalitatea, avand media
aritmetica,  , egala cu media aritmetica a populatiei,
, egala cu media aritmetica a populatiei, 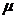 . Stim ca toate curbele normale contin
aproximativ 68% din cazuri intre 1Z, 95%
din cazuri intre 2Z si
98% din cazuri intre 3Z
fata de medie. Aici, cazurile sunt medii aritmetice ale
esantioanelor, astfel ca exista o probabilitate mare
(aproximativ 68 de sanse din 100) ca media aritmetica a
esantionului considerat, 5000000, sa se afle intre 1Z, o probabilitate foarte mare (95 din 100)
ca aceasta medie sa se afle intre 2Z si o probabilitate extrem de mare (98 din
100) ca aceasta medie sa se afle intre 3Z fata de media aritmetica a
distributiei de esantionare
. Stim ca toate curbele normale contin
aproximativ 68% din cazuri intre 1Z, 95%
din cazuri intre 2Z si
98% din cazuri intre 3Z
fata de medie. Aici, cazurile sunt medii aritmetice ale
esantioanelor, astfel ca exista o probabilitate mare
(aproximativ 68 de sanse din 100) ca media aritmetica a
esantionului considerat, 5000000, sa se afle intre 1Z, o probabilitate foarte mare (95 din 100)
ca aceasta medie sa se afle intre 2Z si o probabilitate extrem de mare (98 din
100) ca aceasta medie sa se afle intre 3Z fata de media aritmetica a
distributiei de esantionare  , care are aceeasi valoare cu
, care are aceeasi valoare cu 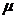 :
:
Figura 6.1 Procente din aria de sub curba normala
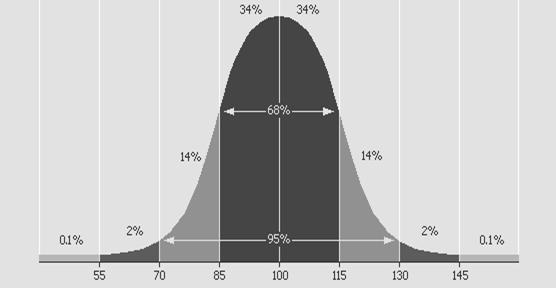
De remarcat ca in aproximativ 2% din cazuri, media
aritmetica de 5000000 se afla la mai mult de 3Z fata de media aritmetica a
distributiei de esantionare. Practic, putem spune ca media
aritmetica de 5000000 nu se afla in acea "minoritate".
Cea de-a doua
conditie pe care trebuie sa o satisfaca un estimator,
eficienta, este legata de dispersie. Un estimator este cu atat mai eficient,
cu cat distributia de esantionare este mai grupata in jurul
mediei sale aritmetice sau, altfel spus, cu cat este mai mica abaterea
standard a distributiei de esantionare. Sa consideram
mediile aritmetice ale esantioanelor. Din teorema limitei centrale
stim ca abaterea standard a distributiei de esantionare a
mediilor aritmetice ale esantioanelor,  , este egala cu
, este egala cu 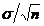 , deci
, deci  este invers
proportionala cu n: cu cat dimensiunea esantionului este
mai mare, cu atat este mai mica
este invers
proportionala cu n: cu cat dimensiunea esantionului este
mai mare, cu atat este mai mica  . Ca atare, eficienta mediei aritmetice ca estimator
poate fi imbunatatita (=
. Ca atare, eficienta mediei aritmetice ca estimator
poate fi imbunatatita (= poate fi micsorata) prin marirea dimensiunii
esantionului. Pentru ilustrare, sa consideram urmatorul
exemplu:
poate fi micsorata) prin marirea dimensiunii
esantionului. Pentru ilustrare, sa consideram urmatorul
exemplu:
|
Esantionul 1
|
Esantionul 2
|
|

|

|
|
n1 = 100
|
n2 = 1000
|
Sa presupunem ca abaterea standard a populatiei, σ,
este de 275000 (evident, valoarea lui σ este rareori cunoscuta
in realitate). In privinta primului esantion, abaterea standard a
distributiei de esantionare a mediilor aritmetice ale tuturor
esantioanelor cu n = 100 este  = 27500. In privinta celui de-al doilea esantion,
abaterea standard a distributiei de esantionare a mediilor aritmetice
ale tuturor esantioanelor cu n = 1000 este considerabil mai
mica:
= 27500. In privinta celui de-al doilea esantion,
abaterea standard a distributiei de esantionare a mediilor aritmetice
ale tuturor esantioanelor cu n = 1000 este considerabil mai
mica: 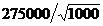 = 8697. Cea de-a doua distributie de esantionare
este mult mai grupata decat prima distributie.
= 8697. Cea de-a doua distributie de esantionare
este mult mai grupata decat prima distributie.
Rezumand, intrucat  este invers
proportionala cu n, cu cat esantionul este mai mare, cu
atat distributia de esantionare este mai grupata si
eficienta estimatorului este mai mare.
este invers
proportionala cu n, cu cat esantionul este mai mare, cu
atat distributia de esantionare este mai grupata si
eficienta estimatorului este mai mare.

![]() , este egala cu media aritmetica a populatiei,
μ. Statisticienii au demonstrat ca si proportiile
esantioanelor, p, sunt nedistorsionate, intrucat media
aritmetica a distributiei de esantionare a proportiilor
pentru esantioane, μp, este egala cu
proportia populatiei, P. Prin contrast, un estimator este distorsionat,
daca media aritmetica a distributiei sale de esantionare
este diferita de media aritmetica a populatiei. De pilda,
abaterea standard a unui esantion este un estimator distorsionat al
abaterii standard a populatiei: de regula, dispersia unui
esantion este mai mica decat cea a populatiei de
referinta, astfel ca s tinde sa subestimeze pe σ.
Dupa cum am mentionat in capitolul 3, aceasta distorsiune poate
fi corectata.
, este egala cu media aritmetica a populatiei,
μ. Statisticienii au demonstrat ca si proportiile
esantioanelor, p, sunt nedistorsionate, intrucat media
aritmetica a distributiei de esantionare a proportiilor
pentru esantioane, μp, este egala cu
proportia populatiei, P. Prin contrast, un estimator este distorsionat,
daca media aritmetica a distributiei sale de esantionare
este diferita de media aritmetica a populatiei. De pilda,
abaterea standard a unui esantion este un estimator distorsionat al
abaterii standard a populatiei: de regula, dispersia unui
esantion este mai mica decat cea a populatiei de
referinta, astfel ca s tinde sa subestimeze pe σ.
Dupa cum am mentionat in capitolul 3, aceasta distorsiune poate
fi corectata.![]() . Dupa cum am aratat, variabila venit
prezinta o distributie asimetrica. Cu toate acestea, conform
teoremei limitei centrale, distributia de esantionare a
. Dupa cum am aratat, variabila venit
prezinta o distributie asimetrica. Cu toate acestea, conform
teoremei limitei centrale, distributia de esantionare a ![]() pentru esantioane mari (n 100) aproximeaza normalitatea, avand media
aritmetica,
pentru esantioane mari (n 100) aproximeaza normalitatea, avand media
aritmetica, ![]() , egala cu media aritmetica a populatiei,
, egala cu media aritmetica a populatiei, ![]() . Stim ca toate curbele normale contin
aproximativ 68% din cazuri intre 1Z, 95%
din cazuri intre 2Z si
98% din cazuri intre 3Z
fata de medie. Aici, cazurile sunt medii aritmetice ale
esantioanelor, astfel ca exista o probabilitate mare
(aproximativ 68 de sanse din 100) ca media aritmetica a
esantionului considerat, 5000000, sa se afle intre 1Z, o probabilitate foarte mare (95 din 100)
ca aceasta medie sa se afle intre 2Z si o probabilitate extrem de mare (98 din
100) ca aceasta medie sa se afle intre 3Z fata de media aritmetica a
distributiei de esantionare
. Stim ca toate curbele normale contin
aproximativ 68% din cazuri intre 1Z, 95%
din cazuri intre 2Z si
98% din cazuri intre 3Z
fata de medie. Aici, cazurile sunt medii aritmetice ale
esantioanelor, astfel ca exista o probabilitate mare
(aproximativ 68 de sanse din 100) ca media aritmetica a
esantionului considerat, 5000000, sa se afle intre 1Z, o probabilitate foarte mare (95 din 100)
ca aceasta medie sa se afle intre 2Z si o probabilitate extrem de mare (98 din
100) ca aceasta medie sa se afle intre 3Z fata de media aritmetica a
distributiei de esantionare ![]() , care are aceeasi valoare cu
, care are aceeasi valoare cu ![]() :
:![]()
![]()

![]()
![]() , este egala cu
, este egala cu ![]() , deci
, deci ![]() este invers
proportionala cu n: cu cat dimensiunea esantionului este
mai mare, cu atat este mai mica
este invers
proportionala cu n: cu cat dimensiunea esantionului este
mai mare, cu atat este mai mica ![]() . Ca atare, eficienta mediei aritmetice ca estimator
poate fi imbunatatita (=
. Ca atare, eficienta mediei aritmetice ca estimator
poate fi imbunatatita (=![]() poate fi micsorata) prin marirea dimensiunii
esantionului. Pentru ilustrare, sa consideram urmatorul
exemplu:
poate fi micsorata) prin marirea dimensiunii
esantionului. Pentru ilustrare, sa consideram urmatorul
exemplu:![]()
![]()
![]() = 27500. In privinta celui de-al doilea esantion,
abaterea standard a distributiei de esantionare a mediilor aritmetice
ale tuturor esantioanelor cu n = 1000 este considerabil mai
mica:
= 27500. In privinta celui de-al doilea esantion,
abaterea standard a distributiei de esantionare a mediilor aritmetice
ale tuturor esantioanelor cu n = 1000 este considerabil mai
mica: ![]() = 8697. Cea de-a doua distributie de esantionare
este mult mai grupata decat prima distributie[1].
= 8697. Cea de-a doua distributie de esantionare
este mult mai grupata decat prima distributie[1].![]() este invers
proportionala cu n, cu cat esantionul este mai mare, cu
atat distributia de esantionare este mai grupata si
eficienta estimatorului este mai mare[2].
este invers
proportionala cu n, cu cat esantionul este mai mare, cu
atat distributia de esantionare este mai grupata si
eficienta estimatorului este mai mare[2].![]() , in timp ce prima distributie contine ce 68% din
mediile aritmetice intr-un interval mult mai larg: 27500.
, in timp ce prima distributie contine ce 68% din
mediile aritmetice intr-un interval mult mai larg: 27500.