TESTUL CHI PATRAT (χ²)

Testul chi patrat (χ²) este aplicabil atunci cand nivelul de masura este nominal, datele fiind frecvente - numarul de cazuri care fac parte din categoriile variabilelor (variabilei) considerate. Esenta acestui test consta din compararea frecventelor observate - frecventele efective obtinute empiric de catre cercetator - cu frecventele teoretice sau asteptate - frecventele calculate sub presupunerea ca ipoteza de nul este adevarata. Testul examineaza masura in care frecventele observate sunt sau nu semnificativ diferite de frecventele care sunt asteptate daca ipoteza de nul este adevarata.

Distinctia dintre frecventele observate si cele asteptate poate fi inteleasa cu ajutorul urmatorului exemplu intuitiv. Sa presupunem ca avem un zar si dorim sa verificam ipoteza ca zarul este nemasluit. Pentru aceasta, aruncam zarul de 300 de ori si observam frecventa de aparitie a fiecarei fete. Daca ipoteza mentionata este adevarata, ne-am astepta ca fiecare fata sa apara de aproximativ 50 de ori. Acum, sa presupunem ca observam urmatoarele frecvente de aparitie:

Comparand frecventele observate cu cele teoretice, suntem indreptatiti sa spunem ca zarul respectiv este masluit sau diferentele pot fi puse pe seama fluctuatiilor intamplatoare?

Testul chi patrat poate fi folosit pentru verificarea independentei a doua variabile sau pentru verificarea concordantei dintre frecventele observate si frecventele asteptate ale unei singure variabile. Corespunzator, se vorbeste despre testul chi patrat pentru independenta si despre testul chi patrat pentru concordanta

1.1 TESTUL CHI PATRAT PENTRU INDEPENDENTA

Doua variabile sunt independente reciproc daca, pentru toate cazurile din esantionul considerat, clasificarea unui caz intr-o categorie a unei variabile nu are nici un efect asupra probabilitatii ca acel caz sa fie clasificat in oricare dintre categoriile celeilalte variabile[1]. De pilda, sa presupunem ca variabilele de interes sunt sexul si dominanta functional operativa a mainilor pentru un esantion de 50 de barbati si 50 de femei. Aceste doua variabile sunt independente reciproc in conditiile in care clasificarea subiectilor in categoriile unei variabile (masculin feminin) nu are nici un efect asupra clasificarii cazurilor in categoriile celeilalte variabile (dreapta, stanga, ambidextru). Acum, sa presupunem ca am efectuat un astfel de studiu si am obtinut urmatoarele date:

Tabelul 1 Sexul si dominanta functional operativa a mainilor

Un astfel de tabel rectangular, in care cazurile dintr-un esantion sunt clasificate concomitent dupa categoriile a doua variabile, se numeste tabel al contingentelor. Denumirile categoriilor unei variabile sunt folosite drept titluri de coloane, iar denumirile categoriilor celeilalte variabile sunt folosite drept titluri de randuri. In corpul tabelului, intersectia unui rand cu o coloana se numeste celula. Celulele indica numarul de cazuri clasificate concomitent in cate doua categorii ale celor doua variabile. Subtotalurile pentru fiecare coloana si rand se numesc marginale. Marginalele indica distributiile de frecvente pentru fiecare categorie a variabilei respective sau, altfel spus, distributiile univariate de frecvente ale fiecarei variabile. La intersectia marginalelor de pe linii si coloane se prezinta numarul total de cazuri din esantion (n).

In cazul testului chi patrat pentru independenta, ipoteza de nul enunta ca variabilele sunt reciproc independente. In exemplul nostru, ipoteza de nul este ca sexul nu are nici o influenta asupra dominantei functional operative a mainilor. Sub supozitia ca ipoteza de nul este adevarata, se calculeaza frecventele din celule la care ne-am astepta, daca ar interveni doar intamplarea. Aceste frecvente asteptate sunt apoi comparate, celula cu celula, cu frecventele observate in tabel. Daca ipoteza de nul este adevarata, atunci diferentele dintre frecventele asteptate si cele observate vor fi mici. Daca, insa, ipoteza de nul este falsa, atunci aceste frecvente vor fi relativ mari. Cu cat sunt mai mari diferentele dintre frecventele asteptate si cele observate, cu atat este mai putin probabil ca variabilele sa fie in fapt reciproc independente si deci este cu atat mai probabil ca vom putea respinge ipoteza de nul.

Pentru a afla frecventa asteptata pentru fiecare celula a tabelului, folosim urmatoarea formula:

Formula 1

in care marginalul randului pe care este situata celula respectiva

marginalul coloanei pe care este situata celula respectiva

n = numarul total de cazuri din esantion

In cazul tabelului 1, frecventele asteptate sunt urmatoarele:

Calcularea statisticii testului chi patrat pentru independenta se face cu ajutorul urmatoarei formule, care da valoarea pentru χ² (obtinut):

Formula 2

in care frecventele observate in celulele tabelului

frecventele asteptate

Astfel, odata calculate frecventele asteptate, formula 2 ne conduce la scaderea frecventei asteptate din frecventa observata pentru fiecare celula, ridicarea la patrat a acestei diferente, impartirea rezultatului la frecventa asteptata pentru acea celula si apoi la insumarea valorilor rezultate ale tuturor celulelor. Calculele pentru exemplul nostru sunt ilustrate in tabelul 2.

Tabelul 2 Calculul χ² pentru datele din tabelul 1

De notat ca suma frecventelor observate este egala cu suma frecventelor asteptate si ca suma diferentelor este egala cu 0. Aceste relatii pot fi folosite la verificarea calculelor pentru χ² (obtinut).

Distributia de esantionare folosita in acest test este distributia χ². Ca si in cazul distributiei t Student, este vorba despre o familie de distributii χ², fiecare fiind o functie de un anumit numar de grade de libertate. In cazul testului chi patrat pentru independenta, numarul de grade de libertate se calculeaza cu ajutorul urmatoarei formule:

Formula 3 gl = (r 1)(c 1)

in care r = numarul de randuri din tabelul contingentelor

c = numarul de coloane din tabelul contingentelor

Un tabel cu trei randuri si doua coloane (un tabel 3 2) are (3 1)(2 1) = 2 grade de libertate[2]. Spre deosebire de distributia t Student, care este simetrica, distributia χ² prezinta, ca si distributia F, o asimetrie pozitiva, dupa cum se ilustreaza in figura 1.

Figura 1 Un exemplu de curba χ²

Valorile pentru χ² (critic) marcheaza inceputurile zonelor critice si sunt date in tabelul valorilor critice ale distributiei χ² (Anexa E). Acest tabel este similar cu tabelul distributiei t Student, avand nivelele α dispuse pe primul rand si gradele de libertate pe prima coloana din stanga. Regula de decizie este

Se respinge H₀, daca χ² (obtinut) > χ² (critic)

Intrucat in exemplu nostru gl = 2, daca stabilim α = 0,05, scorul χ² (critic) este 5,991. Deoarece χ² (obtinut) cade in zona critica (18,00 > 5,991), se poate respinge ipoteza de nul si se poate conchide ca variabilele respective nu sunt reciproc independente: sexul influenteaza dominanta functional operative a mainilor.

In termenii modelului in patru pasi, testul decurge dupa cum urmeaza:

Pasul 1. Enuntarea ipotezelor

H₀: Variabilele sex si dominanta functional-operativa a mainilor sunt reciproc

independente.

H_a: Variabilele sex si dominanta functional-operativa a mainilor sunt reciproc

dependente.

Pasul 2. Selectarea distributiei de esantionare si stabilirea zonei critice

Distributia de esantionare = Distributia χ²

α = 0,05

gl = 2

χ² (critic) = 5,991

Pasul 3. Calcularea statisticii testului. Dupa cum am vazut,

Pasul 4. Luarea deciziei

Intrucat χ² (obtinut) cade in zona critica (18,00 > 5,991), se poate respinge ipoteza de nul si se poate conchide ca variabilele respective nu sunt independente: sexul influenteaza dominanta functional operative a mainilor (la un nivel de incredere de 95%).

1.1 TESTUL CHI PATRAT PENTRU CONCORDANTA

Testul chi patrat poate fi folosit si pentru verificarea concordantei dintre frecventele observate si frecventele asteptate (teoretice) ale unei singure variabile. Astfel, daca χ² (obtinut) > χ² (critic) pentru numarul corespunzator de grade de libertate si un nivel α dat, atunci diferentele dintre frecventele observate si cele asteptate pot fi atribuite intamplarii, concordanta dintre cele doua tipuri de frecvente fiind apreciata drept buna. In caz contrar, diferentele dintre frecventele observate si cele asteptate pot fi considerate prea mari pentru a putea fi atribuite intamplarii sau, altfel spus, aceste diferente sunt statistic semnificative.

Pentru ilustrare, sa presupunem ca un cercetator opineaza ca distributia populatiei dupa ocupatie intr-o anumita zona geografica este aproximativ urmatoarea:

20% tarani

30% muncitori industriali

30% functionari

15% mici intreprinzatori

5% manageri industriali

Cercetatorul alcatuieste un esantion aleatoriu de 864 de persoane ocupate din zona respectiva si le clasifica in categoriile mentionate. Frecventele observate pentru aceste categorii sunt urmatoarele:

145 tarani

310 muncitori industriali

305 functionari

78 mici intreprinzatori

26 manageri industriali

Cercetatorul doreste sa stie daca rezultatele obtinute pe acest esantion confirma distributia presupusa a populatiei sau, altfel spus, daca diferentele dintre frecventele observate si cele presupuse sunt sau nu statistic semnificative. Calcularea statisticii testului se face cu ajutorul formulei 2:

Pentru a afla frecventa asteptata pentru fiecare categorie a variabilei considerate, folosim urmatoarea formula:

Formula 4

in care n = numarul total de cazuri din esantion

p = proportia presupusa de cazuri din categoria respectiva

De pilda, pentru tarani, .

Calculele pentru exemplul nostru sunt ilustrate in tabelul 3.

Tabelul 3 Calculul χ² pentru datele privind ocupatia

De notat ca frecventele asteptate sunt exact acele frecvente pe care le-am intalni daca proportiile cazurilor din esantion ar fi acelasi cu proportiile cazurilor pentru populatie.

In cazul testului chi patrat pentru concordanta, numarul de grade de libertate se calculeaza cu ajutorul urmatoarei formule:

Formula 5 gl = k 1

in care k = numarul de categorii ale variabilei de interes.

Intrucat in exemplul nostru sunt considerate cinci categorii ale variabilei ocupatie, avem patru grade de libertate[3]. Pentru α = 0,05 si gl = 4, χ² (critic) = 9,488.

Testul formal este urmatorul:

Pasul 1. Enuntarea ipotezelor

H₀: Nu exista nici o diferenta intre proportiile din esantion si cele pentru populatie

H_a: Proportiile din esantion difera de cele pentru populatie

Pasul 2. Selectarea distributiei de esantionare si stabilirea zonei critice

Distributia de esantionare = Distributia χ²

α = 0,05

gl = 4

χ² (critic) = 9,488

Pasul 3. Calcularea statisticii testului. Dupa cum am vazut,

Pasul 4. Luarea deciziei

Intrucat χ² (obtinut) cade in zona critica (49,91 > 9,448), se poate respinge ipoteza de nul. Diferentele dintre esantion si populatie sunt prea mari pentru a putea fi atribuite intamplarii (la un nivel de incredere de 95%).

De notat ca, desi aici valoarea pentru χ² (obtinut) este statistic semnificativa, aceasta valoare este calculata tinand cont de toate categoriile, astfel ca nu putem spune care categorie are cea mai mare contributie la semnificatia statistica. Atunci cand avem χ² (obtinut) > χ² (critic), pentru a afla care categorie are cea mai mare contributie la semnificatia statistica, se calculeaza reziduul standard pentru fiecare categorie cu ajutorul urmatoarei formule:

Formula 6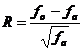

Valorile reziduurilor standard pentru fiecare categorie din exemplul de mai sus se gasesc in tabelul 3. Atunci cand valoarea absoluta (modulul) reziduului standard pentru o categorie este mai mare decat 2,00, se poate conchide ca acea categorie are o contributie majora la valoarea semnificativa a lui χ² (obtinut). In exemplul de mai sus, toate reziduurile standard in valoare absoluta sunt mai mari decat 2,00. Prin urmare, toate categoriile contribuie major la valoarea semnificativa a lui χ² (obtinut), ceea ce inseamna ca intreaga distributie din esantion nu concorda cu distributia presupusa de cercetator.