ANOVA PENTRU DOUA VARIABILE INDEPENDENTE

Testul ANOVA pentru doua variabile independente este o extindere a testului ANOVA pentru o singura variabila independenta, cu exceptia faptului ca formulele testului expus in aceasta sectiune sunt aplicabile doar in cazul grupurilor independente cu acelasi numar de subiecti in fiecare grup. Vom folosi aceeasi maniera de expunere ca mai sus: vom prezenta un exemplu ipotetic, un tabel de calcule initiale, formulele de calcul ale testului ANOVA pentru doua variabile independente, precum si modelul in patru pasi specific acestui test.

20 de elevi sunt supusi unui experiment privind metodele de instruire in matematica. Variabila independenta, A, este, deci, metoda de instruire. Elevii sunt repartizati aleatoriu in doua clase: o clasa la care se utilizeaza metoda traditionala (A1) si o clasa la care se utilizeaza o metoda moderna (A2). Variabila independenta, B, este nivelul IQ, cu categoriile : B1 (< 90) si B2 ( 90). Informatia prezentata la cele doua clase este aceeasi. La sfarsitul perioadei de instruire elevii dau acelasi test. Rezultatul (scorul) obtinut la acest test este variabila dependenta. Experimentul permite evaluarea a trei efecte: (i) efectul principal al variabilei A (daca una dintre metode conduce la rezultate diferite fata de cealalta), (ii) efectul principal al variabilei B (daca elevii cu un IQ superior obtin rezultate diferite fata de ceilalti), (iii) interactiunea A B (daca efectul unei variabile independente difera in functie de un anumit nivel al celeilalte variabile independente).

Dupa cum reiese si din cele de mai sus, un astfel de experiment are mai multe avantaje. Mai intai, prin analiza simultana a doua variabile independente se realizeaza, de fapt, doua cercetari altfel distincte. Pe langa investigarea modului in care diferitele categorii ale celor doua variabile independente afecteaza variabila dependenta, se poate verifica daca nivelele uneia dintre variabilele independente afecteaza variabila dependenta in acelasi fel ca si nivelele celeilalte variabile independente. Apoi, este vorba despre investigarea interactiunii dintre doua variabile independente. Intrucat, in situatiile reale, efectul unei variabile independente este adesea afectat de una sau mai multe variabile independente, studiul interactiunii dintre variabilele independente poate fi un obiectiv foarte important al cercetarii.

Revenind la exemplul nostru ipotetic, datele obtinute, impreuna cu marimile necesare pentru ANOVA sunt prezentate in urmatorul tabel:

Tabelul 3 Calcule initiale pentru ANOVA, doua variabile independente

In ANOVA pentru doua variabile independente se testeaza trei ipoteze de nul, fiecare corespunzand unei surse de variatie:

H₀₁: La nivelul populatiei nu exista nici o diferenta intre mediile aritmetice ale

rezultatelor obtinute prin cele doua metode.

H₀₂: La nivelul populatiei nu exista nici o diferenta intre mediile aritmetice ale

rezultatelor obtinute de elevii cu nivele IQ diferite.

H₀₃: La nivelul populatiei nu exista interactiune intre cele doua variabile.

H₀₁ corespunde variatiei mediilor aritmetice ale scorurilor variabilei dependente din fiecare categorie a variabilei A. H₀₂ corespunde variatiei mediilor aritmetice ale scorurilor variabilei dependente din fiecare categorie a variabilei B. H₀₃ corespunde variatiei mediilor aritmetice ale scorurilor variabilei dependente din categoriile combinate A B.

In acest caz, se calculeaza cinci sume de patrate: (1) SS_TOTAL, (2) SS_A, (3) SS_B,

(4) SS_{A B} si (5)SS_EROARE.

SS_TOTAL se calculeaza cu ajutorul formulei 1:

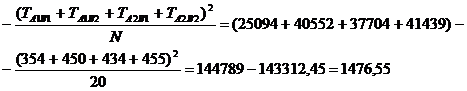
Si aici, atunci cand calculam SS_TOTAL, este recomandabil sa retinem termenii diferentei, 144789 si 143312,45, pe care ii vom folosi pentru simplificarea calculelor ulterioare.

Formula 2 este modificata corespunzator pentru calculul SS_A si SS_B. Astfel, SS_A se calculeaza cu ajutorul urmatoarei formule:

Formula 7

In aceasta formula, T_a este un simbol general pentru T_A1 si T_A2, iar n_a este un simbol general pentru n_A1 si n_A2. Prin urmare, atunci cand calculam SS_A, luam in considerare doar grupurile variabilei independente A.

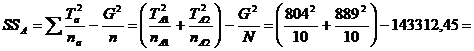
SS_B se calculeaza cu ajutorul urmatoarei formule:

Formula 8

In aceasta formula, T_b este un simbol general pentru T_B1 si T_B2, iar n_b este un simbol general pentru n_B1 si n_B2. Prin urmare, atunci cand calculam SS_B, luam in considerare doar grupurile variabilei independente B.

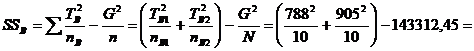
Calculam acum SS_{A B}, cu ajutorul urmatoarei formule:

Formula 9

In aceasta formula, T_ab este un simbol general pentru T_A1B1, T_A1B2, T_A2B1 si T_A2B2, iar n_ab este un simbol general pentru n_A1B1, n_A1B2, n_A2B1 si n_A2B2. Prin urmare, atunci cand calculam SS_{A B}, luam in considerare grupurile constituite dupa categoriile combinate

A B.

=

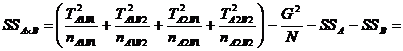
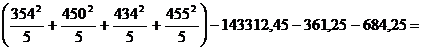
Si aici vom retine unul dintre termenii diferentei, si anume 144639,40, pe care il vom folosi pentru calculul SS_EROARE, dupa urmatoarea formula:

Formula 10

Ambele cantitati cerute de aceasta formula au fost calculate anterior, cand am obtinut SS_TOTAL si, respectiv, SS_{A B}, asa incat vom prelua direct rezultatele respective in calculul SS_EROARE:

De notat ca SS_TOTAL = SS_A + SS_B + SS_{A B} + SS_EROARE. Aceasta relatie poate fi utilizata pentru a controla corectitudinea calculelor.

Mediile aritmetice ale sumelor de patrate pentru fiecare sursa de varianta se calculeaza prin impartirea sumei de patrate respectiva la numarul corespunzator de grade de libertate.

Formula 11

In aceasta formula, k_A este numarul de grupuri constituite dupa categoriile variabilei A, iar k_A - 1 este numarul de grade de libertate asociate SS_A, notat cu gl_A. In exemplul nostru,

Formula 12

In formula 12, k_B - 1 este numarul de grupuri constituite dupa categoriile variabilei B, iar k_B - 1 este numarul de grade de libertate asociate SS_B, notat cu gl_B. In exemplul nostru,

Formula 13

In formula 13, (k_A - 1)(k_B - 1) este numarul de grade de libertate asociat SS_{A B}, notat cu gl_{A B}. In exemplul nostru,

Formula 14

In formula 14, N - k_Ak_B este numarul de grade de libertate asociat SS_EROARE, notat cu gl_EROARE.

Valoarea pentru F (obtinut) se calculeaza pentru fiecare sursa de varianta sistematica (efectele principale pentru A, pentru B si pentru interactiunea A B). Prezentam in continuare formulele de calcul pentru F_A (obtinut), F_B (obtinut) si F_{A B} (obtinut), impreuna cu calculele respective, corespunzatoare exemplului nostru.

Formula 15

Formula 16

Formula 17

Pentru luarea deciziei, fiecare valoare pentru F (obtinut) se compara cu F (critic). Intrucat in fiecare caz din exemplul nostru, gl_EROARE = 16, iar numarul de grade de libertate din numarator pentru media aritmetica este egal cu 1 (gl_A = gl_B = gl_{A B} = 1), pentru α = 0,05, F (critic) = 4,4940 sau, rotunjit, 4,49[1]. Deoarece fiecare F (obtinut) este mai mare decat F (critic), toate cele trei ipoteze de nul pot fi respinse. De notat ca toate cele trei ipoteze de nul pot fi respinse (rezultatele experimentului sunt semnificative) si pentru α = 0,01, pentru care F (critic) = 8,53.

In termenii modelului in patru pasi, testul ANOVA pentru doua variabile independente decurge astfel:

Pasul 1 Enuntarea ipotezelor

H₀₁: La nivelul populatiei nu exista nici o diferenta intre mediile aritmetice ale rezultatelor obtinute prin cele doua metode.

H_a1: La nivelul populatiei mediile aritmetice ale rezultatelor obtinute prin cele doua metode difera.

H₀₂: La nivelul populatiei nu exista nici o diferenta intre mediile aritmetice ale rezultatelor obtinute de elevii cu nivele IQ diferite.

H_a2: La nivelul populatiei mediile aritmetice ale rezultatelor obtinute de elevii cu nivele IQ diferite difera.

H₀₃: La nivelul populatiei nu exista interactiune intre cele doua variabile.

H_a3: La nivelul populatiei exista interactiune intre cele doua variabile.

Pasul 2 Selectarea distributiei de esantionare si stabilirea zonelor critice.

Distributia de esantionare = distributia F

α = 0,05

gl_EROARE = 16

gl_A = gl_B = gl_{A B} = 1

F (critic) = 4,49

Pasul 4 Calcularea statisticii testului

Organizarea calculului ANOVA pentru doua variabile independente se face cu ajutorul unui tabel de calcule initiale (v. tabelul 3), precum si al unui tabel ANOVA rezumativ (tabel al surselor de variatie). In acest caz, forma generala a unui astfel de tabel este urmatoarea:

In exemplul nostru, avem urmatorul tabel:

Tabelul 4 ANOVA rezumativ, doua variabile independente

Pasul 4 Luarea deciziei

Intrucat fiecare valoare pentru F (obtinut) este mai mare decat valoarea pentru F (critic), se resping cele trei ipoteze de nul. Pentru efectul principal al variabilei A, concluzia este ca la nivelul populatiei, mediile aritmetice ale rezultatelor obtinute prin cele doua metode difera semnificativ. Pentru efectul principal al variabilei B, concluzia este ca la nivelul populatiei, mediile aritmetice ale rezultatelor obtinute de elevii cu nivele IQ diferite difera semnificativ. Enuntul de probabilitate asociat ambelor concluzii este urmatorul: probabilitatea ca diferentele observate intre mediile aritmetice ale grupurilor constituite dupa categoriile unei variabile independente sa apara din intamplare, daca H₀ respectiva ar fi in realitate adevarata, este mai mica de 0,05 (si dupa cum am vazut, chiar decat 0,01).

Pentru interactiune, concluzia este ca la nivelul populatiei exista o interactiune intre metoda de instruire si nivelul IQ al subiectilor. Enuntul de probabilitate asociat acestei concluzii este urmatorul: probabilitatea ca diferentele observate intre mediile aritmetice ale scorurilor din categoriile combinate ale celor doua variabile sa apara din intamplare, daca H₀₃ ar fi in realitate adevarata, este mai mica de 0,05 (si decat 0,01).