
|
|
|
O particula in miscare de rotatie e caracterizata de un moment cinetic (L), vector perpendicular pe planul traiedtoriei, dependent de masa si viteza particulei si raza traiectoriei, deci descrie caracteristicile miscarii: L~mvr.
O sarcina electrica in miscare este influentata de un camp magnetic, deci se comporta ca un mic magnet, caracterizat printr‑un moment magnetic. Momentul magnetic e tot un vector perpendicular pe planul traiectoriei, sensul depinnzad de semnul sarcinii.

Electronul are
un moment cinetic si, respectiv, un moment magnetic orbital,
corespunzator rotatiei in jurul nucleului, dar si un moment
cinetic si, respectiv, un moment magnetic de spin. Acestea din urma
ar putea fi interpretate intuitiv ca fiind corespunzatoare unei
miscari de rotatie in jurul propriei axe. In mecanica
cuantica, momentul cinetic de spin sau spinul (S) e cuantificat, depinzand
de numarul cuantic de spin (s), ![]() , ce poate lua valorile
, ce poate lua valorile ![]() Momentul magnetic
corespunzator (de spin) are valoarea:
Momentul magnetic
corespunzator (de spin) are valoarea:
![]() ; [μ]=J/T
; [μ]=J/T
unde: γ=e/2m=raport giromagnetic;
g=factorul lui Landé, constanta ce depinde de natura particulei;
h=constanta lui Plank;
S=moment cinetic de spin;
s=munar cuantic de spin, s=1/2,-1/2.
Momentul magnetic se masoara in joule/tesla (J/T).
Marimea μB γh/2π=he/4πme se numeste magnetonul lui Bohr (me=masa electronului) se poate considera o cuanta de moment magnetic. In mod similar protonul are si el moment magnetic de spin. Se defineste magnetonul nuclear, μN=hγN/2π=he/4πmp, in care s‑a inlocuit masa electronului cu a protonului (mp); γN este raportul giromagnetic al protonului. Magnetonul nuclear e cu trei ordine de marime mai mic decat magnetonul lui Bohr deoarece masa protonului este mai mare. Se constata si se demonstreaza In mecanica cuantica faptul, inexplicabil in cadrul mecanicii clasice, ca neutronul, desi neutru, are totusi un moment magnetic de spin, egal cu al protonului. Ca si in cazul electronului, nucleolii se asociaza in perechi de spin opus (+1/2 si -1/2), astfel incat pentru un numar par, spinil total e nul.
Pentru un nucleu, cuprinzand un numar Z de protoni si A-Z neutroni, momentul magnetic de spin total se obtine prin insumarea momentelor corespunzatoare protonilor si, respectiv, neutronilor. Sunt posibile trei cazuri:
atat protonii cat si neutronii sunt in numar par (A si Z pare); rezulta un spin nul;
numarul de masa (A) e impar, deci fie protunii, fie neutronii, sunt in numar impar; rezulta un spin semiintreg (+1/2 sau -1/2);
A e par si Z impar, ceea ce inseamna ca atat protonii cat si neutronii sunt in numar impar; spinil este intreg (1), deoarece spinul semiintreg rezultat pentru fiecare tip de nucleoni in parte se aduna, dand 1.
Daca o particula, avand un moment magnetic nenul, e plasata in camp magnetic (B), asupra ei se exercita un cuplu de forte, ceea ce imprima o miscare de precesie, precesia Larmour, avand ca ax directia campului magnetic, in urma careia se va orienta pe directia lui B. E o miscare similara cu a unui titirez. Viteza unghiulara (ωL) si, respectiv, frecventa (νL) miscarii de presesie sunt date de relatiile:
ωL=gγB; νL ωL/2π=g(γ/2π)B.
Inmultind frecventa cu constanta lui Plank, se regaseste expresia magnetonului. Deci
hνL=g(γh/2π)B=gμBB pentru electron
hνL=gN(γNh/2π)B=gNμNB pentru un proton.
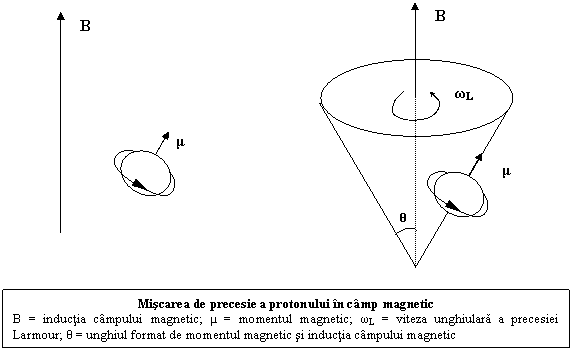
Deci νL, frecventa
Larmoure a protonului, e
proportionala cu inductia campului magnetic si cu
magnetonul nuclear. Ea este de ordinul
MHz, asadar in domeniul de radiofrecventa.
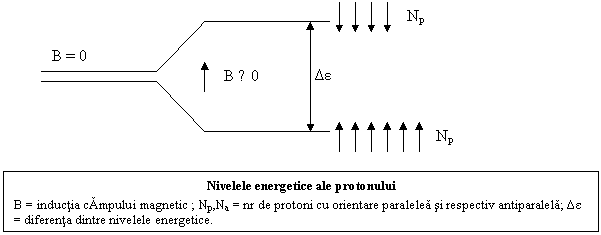
Daca o particula avand un moment magnetic se plaseaza intr-un camp magnetic uniform de inductie B, ea va avea o energie potentiala ε μB=-gNμNBs.
Comparand aceasta relatie cu expresia frecventei Larmoure, rezulta ca la o variatie a numarului cuantic de spin cu 1 unitate (intre -1/2 si +1/2), energia variaza cu Δε=hνL
Deci intr-un camp magnetic, protonul se poate afla in doua stari
energetice, cea mai joasa corespunzand spinului +1/2. Cele doua
stari reprezinta o orientare paralela (p), respectiv,
antiparalela (a), cu directia campului. La echilibru, intr-o
populatie de protoni, repartitia pe cele doua nivele este data
de relatia lui Boltzmann: ![]() , in care:
, in care:
Np si Na reprezinta numarul de protoni aflati pe cele doua nivele (paralel, respectiv antiparalel).
B=inductia campului magnetic;
k=constanta lui Boltzmann;
h=constanta lui Plank;
T=temperatura absoluta.
Raportul are o
valoare putin mai mare decat 1, deci pe nivelul fundamental se afla
mai putini protoni. In consecinta, la echilibru, μN rezultant e paralel
cu inductia campului magnetic (B).
Pentru ca un proton sa treaca de pe nivelul fundamental pe nivelul excitat, trebuie sa i se furnizeze o energie egala cu Δε. Deci el poate absorbi o radiatie electromagnetica de frecventa egala cu frecventa Larmoure; este frecventa de rezonanta. Supa cum reiese din relatiile de mai sus, aceasta frecventa e proportionala cu inductia campului magnetic B.
O populatie de nuclee cu spin nenul, plasata intr‑un camp magnetic uniform si constant se repartizeaza, asa cum am vazut intre cele doua nivele energetice conform legii lui Boltzman. Daca peste acest camp se suprapune un camp electromagnetic cu frecventa Larmour, spinii absorb energia si pot trece rapid pe nivelul energetic superior; ei intra in rezonanta cu campul EM. Reorientarea spinilor induce o tensiune electromoroare intr‑o infasurare ce inconjoara proba. Aplicandu‑se un camp electromagnetic de frecventa variabila continuu (in domeniul de radiofrecventa), fiecare specie nucleara cuprinsa in esantion va intra in rezonanta la propria frecventa Larmour (ν=νL); s‑a realizat astfel un baleiaj de frecventa. Inregistrandu‑se semnalul se obtine spectrul RMN, A(ν); frecventa liniilor spectrale corespunde frecventei Larmour a nucleelor, iar amplitudinea numarului de nuclee care absorb la frecventa respectiva.
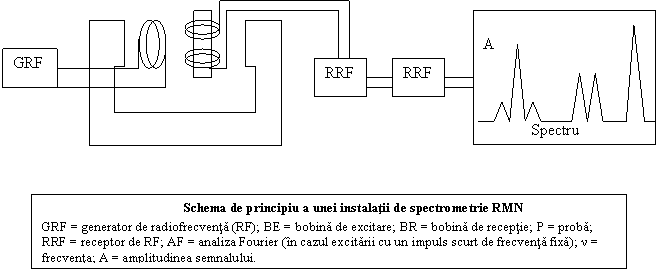
Operatia se poate realiza
si altfel: campul EM aplicat are o frecventa constanta, dar
peste campul B se aplica un al doilea camp, de intensitate mult mai
mica (ΔB) si reglabil. Rezonanta se obtine pentru gNμN(B+ΔB)=hνL. S‑a facut
un baleiaj de camp.
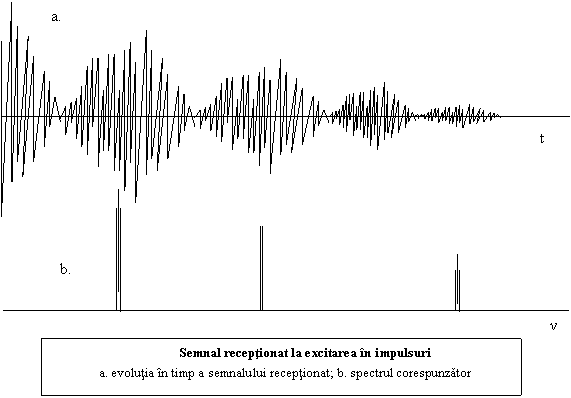
In prezent,
spectrele RMN se obtin prin aplicarea unui semnal de radiofrecventa
sub forma unor impulsuri scurte (μs), de frecventa fixa. Acestea induc o perturbare a
spinilor. Dupa incetarea impulsului, ei revin in situatia de
echilibru, printr‑o precesie Larmour libera, corespunzand unui
semnal sinusoidal amortizat, specific pentru fiecare specie nucleara
prezenta. Se inregistreaza raspunsul sistemului ca o
functie de timp f(t). Printr‑o transfirmare Fourier se obtine
spectrul A(ν) al sistemului.
Frecventa
Larmour, depinzand de inductia campului magnetic in imediata
vecinatate a nucleului, e influentata de campurile magnetice ale
altor nuclee prezente si de norul electronic ce inconjoara nucleul.
Acesta realizeaza o ecranare, ce se manifesta prin faptul ca
nucleul "simte" un camp magnetic nai nic decat cel aplicat (B). Consecinta
va fi o deplasare a frecventei de rezonanta fata de
cea a nucleului izolat. Deplasarea e de ordinul 10-6 din
frecventa de rezonanta si se exprima in parti pe milion (ppm=10-6).
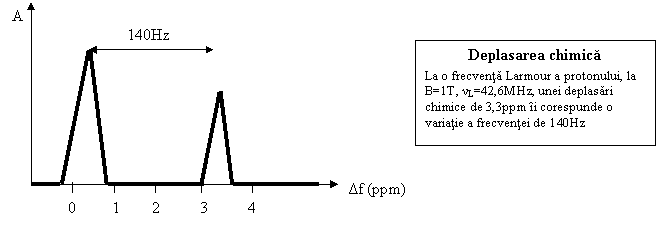
Deplasarea poate da indicatii asupra mediului ambiant. De exemplu,
frecventa de rezonanta a protonilor in grasimi e
deplasata fata de cea in apa cu 3,3ppm. La B=1T,
frecventa Larmour a protonilor fiind 42,6MHz corespunde unei
deplasari de 140Hz. Exprimarea in ppm are avantajul ca nu depinde de
intensitatea campului.
La excitarea cu un camp de RF a macromoleculelor, interactiunile dintre protoni sunt multiple, deci spectrele ce se obtin sunt extrem de complexe, multe linii spectrale suprapunandu‑se, asa ca devine destul de dificil de extras informatia. Acest lucru este inlaturat prin spectroscopia bidimensionala. Extitarea se face in secvente. Intr‑o prima etapa, proba este iradiata cu un semnal de RF care va excita toate nucleele. Fiecare insa va avea o precesie cu o frecventa ce depinde de campul local, deci de interactiunile la care ia parte. Dupa un timp t1 variabil in trepte, cand spinii var fi defazati in functie de propria frecventa Larmour, se aplica un al doilea semnal de RF, care va avea, evident, efecte diferite asupra fiecarui spin. Dupa un timp t2, timpul de achizitie, se inregistreaza raspunsul. Operatia se repeta pentru diferite valori ale lui t1, asteptandu‑se, de fiecare data, revenirea in starea de repaus. Prin analiza Fourier a raspunsurilor inregistrate, s(t1,t2), se obtine spectrul bidimensional, functie de doua variabile de frecventa, ν1 si ν2, corespunzatoare timpilor t1 si t2. Spectrul va cuprinde o serie de varfuri aflate pe diagonala, reprezentand spectrul unidimensional, dar si alte varfuri, asezate simetric fata de dagonala. Acestea indica interactiunile dintre protoni: un varf avand coordonatele (νa νb) si simetricul lui de coordonate (νb νa) indica interactiunea dintre un nucleu cu frecventa de rezonanta νa si unul cu frecventa νb Spectroscopia RMN bidimensionala e foarte utila pentru determinarea structurii proteinelor si a altor macromolecule biologice.