Postulatele mecanicii cuantice ondulatorii

Postulatele mecanicii cuantice ondulatorii.

La baza noii mecanici stau cateva postulate generale, a caror valabilitate este conferita prin confirmarea experimentala a concluziilor ce decurg din aplicarea lor. Aceste postulate nu sunt unice, nu formeaza un cadru formal logic, dar scot in evidenta caracterul abstract si matematic al mecanicii cuantice ondulatorii.

Postulatul 1. Starea la momentul t a unui sistem format din N particule este descrisa in intregime de o functie matematica numita functie de unda sau functie de stare a sistemului ; q defineste setul celor 3N coordonate ale sistemului la momentul t.

Functiile de stare sunt functii regulare ce apartin spatiului Hilbert, avand proprietati rezonabile cerute de sistemele reale. Sunt functii ale unor variabile reale, univoce, continue, derivabile, marginite si de patrat integrabile. Aceasta ultima proprietate inseamna ca integrala patratului modului functiei, extinsa asupra intregului domeniu de definitie, exista si este legata de semnificatia statistica data undelor de Broglie de catre Max Born.

Conform acestei semnificatii atata timp cat variabilele, observabilele (proprietatile masurabile ale sistemului) sunt reale, functiile de unda in sine pot sa nu aiba o semnificatie fizica. Lucrul acesta este evident, aceste functii fiind in general functii complexe. Ceea ce are semnificatie este tocmai patratul modulului functiei de unda, adica produsul , caruia Max Born ii atribuie semnificatia de densitate de probabilitate. Cantitatea:

(I.3)

unde este complex conjugata functiei , reprezinta deci probabilitatea de a gasi sistemul in elementul de volum .

Prin integrarea relatiei (I.3) pe intreg spatiu se va obtine probabilitatea ca cele N particule ale sistemul sa se gaseasca undeva in spatiu, care evident va fi egala cu unitatea:

(I.4)

Relatia (I.4) se mai numeste dat fiind semnificatia ei si conditia de normare la unitate a functiei , conditie ce se impune oricarei functii de stare.

In situatia in care relatia (I.4) nu este indeplinita se procedeaza la normarea functiei prin inmultirea sa cu o constanta de normare N. Astfel functia este inlocuita cu functia normata in care N este constanta de normare

O alta conditie ce poate fi impusa functiilor de stare si care conduce la o simplificare a calculelor este conditia de ortogonalitate a functiilor data de relatia:

(I.5)

Cele doua conditii, de normare si de ortogonaliate, pot fi scrise sub forma conditiei de ortonormare:

(I.6)

unde reprezinta simbolul Kronecker: = 1, pentru i = j si = 0, pentru .

Postulatul 2. Fiecarei marimi fizice M i se asociaza in mecanica cuantica ondulatorie un operator M liniar si hermitic (autoadjuct).

Prin operator se intelege o operatie matematica care se efectueaza asupra unei functii conducand la o alta functie; proprietatea unui operator M de a fi liniar defineste modul de aplicarea a operatorului asupra unei sume de functii, precum si asupra unui produs dintre o constanta si o functie. Aceasta proprietate este data de relatia:

(I..7)

unde c_i sunt constante.

Un operator este hermitic daca este indeplinita relatia:

(I.8)

in care membrul drept este autoadjunctul membrului stang. Relatia (I.8) face ca numai acei operatori care o indeplinesc, sa poata fi asociati unor marimi fizice reale.

Aceasta conditie impusa operatorilor momentan pare mai putin clara. Pentru a intelege semnificatia relatiei (I.8) trebuie aratat ca exista cazuri in care aplicarea operatorului asupra unei functii are ca rezultat reproducerea functiei pana la o constanta:

(I.9)

Ecuatia (I.9) este o ecuatie de functii (vectori) si valori proprii. Daca aceasta ecuatie este indeplinita se spune ca sunt functii (vectori) proprii, iar valorile proprii operatorului M. Totalitatea valorilor proprii ale unui operator alcatuiesc un spectru a operatorului ce poate fi continuu sau discontinuu. In mecanica ondulatorie spectrele operatorilor hermitici sunt discontinui.

Folosind ecuatia (I.9) integrala din membrul stang al relatiei (I.9) devine:

(I.10)

si cum functia proprie este normata se obtine:

(I.11)

Deoarece complex conjugata ecuatiei (I.9) este:

(I.12)

folosind un rationament similar, integrala din membrul drept al relatiei (I.9) devine egala cu:

(I.13)

Cum cele doua integrale sunt egale, M fiind hermitic, rezulta ca . Deoarece un numar poate fi egal cu complexul sau conjugat numai daca numarul este real, rezulta ca operatorii hermitici vor avea intotdeauna numai valori proprii reale.

Operatorii mecanicii cuantice, introdusi prin postulat sunt:

operatorii asociati coordonatelor carteziene x, y, z si timpului t constau in inmultirea functiei cu coordonata, respectiv cu timpul:

; (I.14)

operatorii asociati componentelor impulsului p_x, p_y, p_z sunt definiti prin:

(I.15)

operatorii asociati oricarei alte marimi fizice se obtin prin inlocuirea in expresia clasica a marimii respective a operatorilor coordonatelor, timpului si impulsului.

Astfel operatorul energiei totale numit hamiltonian, notat cu H, se obtine inlocuind operatorii asociati coordonatelor si impulsului in expresia energie totale a sistemului respectiv, data de suma energiei cinetice si potentiale.

Postulatul 3. Daca M este operatorul asociat marimii dinamice M atunci este satisfacuta ecuatia de functii si valori proprii:

functia proprie va fi functie de stare a sistemului, iar valoarea proprie m_i va fi valoarea constanta pe care marimea M o are in aceasta stare.

Conform acestui postulat daca este functie proprie operatorului hamiltonian H asociat energiei sistemului este valabila ecuatia:

(I.16)

numita ecuatia stationara a lui Schrödinger; aceasta ecuatie este o ecuatie diferentiala de gradul doi prin a carei rezolvare se pot obtine functiile de stare ale sistemului, precum si valorile energiilor E_i corespunzatoare aceste stari.

Daca se cunosc functiile de stare si aceste functii de stare sunt functii proprii mai multor operatori, atunci valorile marimilor respective in starile respective vor fi date de relatia:

(I.17)

relatie ce se obtine din ecuatia (I.9) careia postulatul 3 ii da o semnificatie fizica , prin inmultirea ecuatiei la stanga si la dreapta cu , respectiv cu elementul de volum d(q), urmata apoi de integrare:

Postulatul 4. Functiile de stare dependente de timp satisfac ecuatia generalizata la lui Schrödinger:

(I.18)

Aceasta ecuatie este respectata de sistemele cuantice a caror evolutie depinde de timp.

Postulatul 5 Daca M este operatorul asociat marimii fizice M , iar 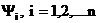sunt functiile proprii acestui operator cu valorile proprii m_i corespunzatoare, atunci si o combinatie liniara a acestor functii proprii:

                  (I.19)

_{va fi functie de stare a sistemului. Probabilitatea ca in aceasta stare valoarea marimii M sa fie mi este data de produsul ci*. ci .}

_{O consecinta a acestui postulat este aceea ca integrala de tip (I.17) capata semnificatia de valoare medie a marimii M:}

(I.20)

I.1.1 Aplicatii

1. Sa se normeze functia de stare a atomului de hidrogen in stare fundamentala, functia nenormata fiind .

Rezolvare:

Functia de stare normata este .

Aceasta functie trebuie sa respecte relatia (I.4).

Se scrie elementul de volum d(q) in coordonate sferice: d(q) = ,

iar relatia (I.4) devine:

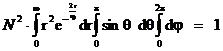
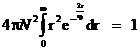
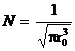
( pentru rezolvarea integralei in r se foloseste: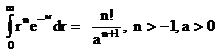

Rezulta:

2. Sa se defineasca hamiltonianul unei particule de masa m care se misca intr-un camp avand energia potentiala V(x,z,y)

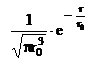
Rezolvare:

Functia Hamilton clasica este: H = T + V operatorul hamiltonian va fi H= T + V

- Energia cinetica T a particulei se scrie in functie de componentele impulsului:

,

iar operatorul corespunzator se obtine prin inlocuirea componentelor impulsului cu operatorii corespunzatori:

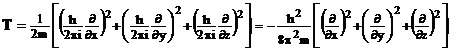
unde reprezinta laplasianul definit ca: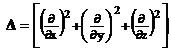

- Energia potentiala V(x,y,z) depinzand doar de coordonatele carteziene operatorul V va consta in inmultirea cu expresia respectiva;

- Hamiltonianul asociat particulei H va fi:

3. Sa se defineasca hamiltonianul unei molecule poliatomice cu n electroni si N nuclee.

Rezolvare:

- Hamiltonianul va contine termenii de energie cinetica si energie potentiala a celor n electroni si N nuclee:

Energia cinetica a nucleelor: 

Energia cinetica a electronilor:                               

Energia de atractie electron-nucleu:                      

Energia potentiala de repulsie a electronilor: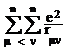      

Energia potentiala de repulsie a nucleelor: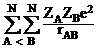

4. Sa se scrie ecuatia lui Schrödinger pentru un sistem polielectronic.

Rezolvare:

In ecuatia (I.16) se introduce expresia hamiltonianului obtinut in aplicatia 3.