|
|
|
Legatura spatiu-timp prin ecuatii parametrice
Observatie: pentru simplificare vom arata aceasta legatura in cazul unei traiectorii liniare plane.
Ecuatia unei drepte in plan este:
(4.2)
unde: m este panta dreptei ,iar n este taietura. Aceasta este forma explicita de scriere .
In geometria analitica se cunosc si alte forme de reprezentare a ecuatiei unei drepte. Dintre acestea ne intereseaza ecuatiile parametrice ale dreptei:
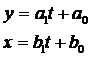(4.13)
unde t este un parametru arbitrar scalar.
Observatie: eliminand t din sistemul (4.13) se ajunge la forma ecuatiei (4.2) pentru dreapta.
La fel, se poate scrie si un sistem de ecuatii de gradul 2 :
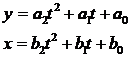(4.14)
sau:
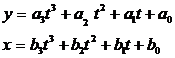(4.15)
, s.a.m.d.
Observatie: se pot scrie si forme cu ecuatii de grad mai mare, singura conditie, in cazul dreptei, fiind aceea ca cele doua ecuatii trebuie sa fie de acelasi grad.
Astfel de ecuatii parametrice exista si pentru alte curbe din plan si spatiu
( sinusoida, curba lantisor, cerc, elipsa, parabola, hiperbola,.).
In general, o curba in spatiu se exprima prin sistemul de ecuatii:
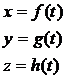(4.16)
unde f, g si h sunt functiile parametrice ale curbei, iar t este un parametru scalar arbitrar.
Sistemul (4.16) este sistemul de ecuatii parametrice ale curbei.
Pentru o dreapta functiile f, g si h sunt de acelasi grad, iar pentru traiectorii de alte forme, au grade diferite.
Pornind de la aceste cunostinte din geometria analitica, in robotica se alege ca parametru scalar t chiar timpul, pentru ca in robotica intereseaza evolutia in timp a miscarii.
Observatii
1). Functiile parametrice sunt intotdeauna polinomiale si, prin urmare, sunt functii line;
2). Daca scalarul t este timpul, atunci functiile parametrice sunt si legi de miscare dupa coordonatele carteziene.
