Placi plane dreptunghiulare

Placi plane dreptunghiulare

1 Incovoierea placilor plane dreptunghiulare

Placile plane dreptunghiulare au o larga raspandire regasindu-se in elementele de carcasa, pereti de rezervoare, elemente din corpul navei, etc.

Calculul acestora este mult mai dificil deoarece parametrii ce reflecta solicitarea, tensiunile si sageata, se determina prin prisma unei functii de doua variabile independente x,y in loc de o variabila r ca in cazul placilor circulare. Functia reflecta deformarea suprafetei mediane si este sub forma unei ecuatii diferentiale cu derivate partiale a carei solutie este data de regula printr-o serie.

In cazul placii dreptunghiulare incarcate cu o sarcina uniform distribuita p normala pe placa, se utilizeaza relatia lui Sophie-Germaine sub forma:

. (XVIII.87)

Rezolvarea ecuatiei (XVIII.87)  este tratata pe larg in literatura de specialitate, in continuare prezentandu-se cateva rezultate finale pentru situatii intalnite frecvent, pentru o sarcina uniform distribuita p normala pe placa de grosimea h.

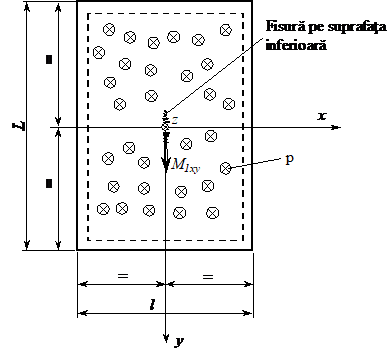
Fig. XVIII.9.a Placa simplu rezemata

Daca placa este simplu rezemata pe contur, fig. (XVIII.9.a), sageata maxima din centrul placii x= y= 0 este:

. (XVIII.88)

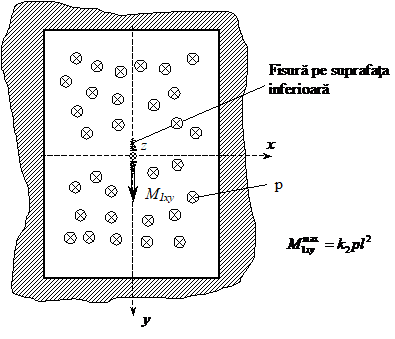
Fig. XVIII.9.b Placa incastrata pe contur

Momentul incovoietor maxim pe unitatea de lungime se dezvolta in centrul placii (x= y= 0) fiind cel care produce rotirea in planul xz (M_1xy), ceea ce inseamna ca fibrele paralele cu latura mai scurta l sunt cele mai solicitate:

, (XVIII.89)

de unde:

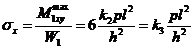. (XVIII.90)

Fisura, la fel ca la placile circulare, se dezvolta in centrul suprafetei inferioare a placii solicitata la tensiuni de intindere din incovoiere.

Coeficientii k₁, k_2, k₃ pentru  cazul cu valoarea coeficientului lui Poisson υ = 0,3 sunt prezentati in tabelul XVIII.1, functii de raportul L/l.

Tabelul XVIII.1. Valoarea coeficientilor k₁, k_2, k₃ in functie de raportul laturilor L/l.

Daca placa este incastrata pe contur (XVIII.9.b) sageata maxima din centru placii x= y= 0 este:

. (XVIII.91)

Momentul incovoietor maxim pe unitatea de lungime are aceeasi orientare ca in cazul placii simplu rezemate M_1xy si se dezvolta in centrul placii x= y= 0.

, (XVIII.92)

de unde,

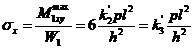. (XVIII.93)

Spre deosebire de placile circulare incastrate fisura se dezvolta in centrul suprafetei inferioare a placii.

Coeficientii k'₁, k'_2, k'₃ sunt prezentate in tabelul XVIII.2, functie de raportul L/l.

Tabelul XVIII.2. Valoarea coeficientilor k'₁, k'_2, k'₃ in functie de raportul laturilor L/l.

2 Incovoierea cilindrica a placilor plane dreptunghiulare

Se considera o placa simplu rezemata pe contur, solicitata cu o sarcina normala pe placa de intensitate constanta pe directia y (directia laturii mari L) si variabila pe directia x. Se constata ca suprafata curbata a placii ia forma unui cilindru avand generatoarea paralela cu axa Oy. Teoretic doar pentru L = ∞ placa se incovoaie cilindric; totusi pentru situatia in care L>3l rezultatele obtinute considerand incovoierea cilindrica a placii sunt acceptabile.

Problema se rezolva si daca se ia placa simplu rezemata numai pe laturile paralele cu directia y, fig.(XVIII.10). Calculul poate fi redus la calculul unei grinzi de latime mare. Studiul se face considerand o fasie izolata avand latimea egala cu o unitate. Aceasta fasie reprezinta o grinda de sectiune transversala dreptunghiulara 1xh de lungime l simplu rezemata,in care se dezvolta efortul moment incovoietor M_1xy cu tensiuni σ_x≠0.

Particularitatea este ca sectiunea transversala a grinzi nu se poate deforma din cauza fasiilor invecinate. In aceasta situatie avem o stare plana de deformare in care:

. (XVIII.94)

Se admite conditia impusa grinzilor, si anume ca materialul nu este solicitat pe directia grosimii placii (inaltimea grinzii), adica:

(XVIII.95)

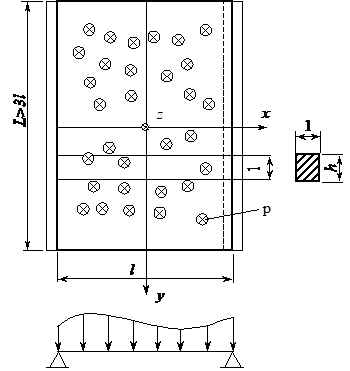
Fig. XVIII.10 Placa simplu rezemata pe laturile paralele

In acest caz legea generalizata a lui Hooke (V.10)  se scrie:

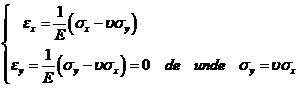(XVIII.96)

Prima ecuatie a sistemului se mai scrie:

, (XVIII.97)

de unde  si , iar E_P este modulul de elasticitate al materialului pentru o fasie de placa.

(XVIII.98)

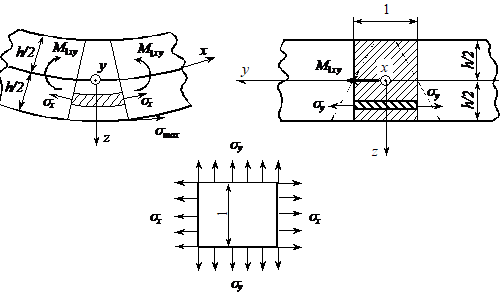
Fig. XVIII.11 Tensiuni in incovoierea cilindrica

Rezulta ca in cazul placii se inlocuieste modulul de elasticitate E cu modulul de elasticitate al materialului pentru o fasie de placa E_P. Astfel ecuatia diferentiala a fibrei medii deformate se scrie:

. (XVIII.99)

Notatia D₁ a fost folosita in relatia  (XVIII.13).

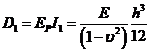(XVIII.100)

In concluzie toate calculele se deruleaza ca la o grinda simplu rezemata de latime egala cu unitatea si de rigiditate E_P.