
|
|
|
Lant cinematic. Mecanism. Grad de mobilitate
Un lant cinematic determinat si inchis se numeste mecanism.
Pentru a se defini, gradul de mobilitate a unui mecanism se pleaca de la notiunea de gradul de libertate al lantului cinematic respectiv.
Gradul de libertate reprezinta numarul parametrilor cinematici independenti care determina miscarea tuturor elementelor lantului.
Daca se noteaza cu e numarul de elemente ale lantului si se considera libere aceste elemente, atunci gradul de libertate ar fi:
![]() (1.3)
(1.3)
Insa elementele sunt legate prin cuple cinematice formand lantul cinematic si tinand seama de faptul ca fiecare cupla de clasa m introduce m conditii de legatura, atunci expresia gradului de libertate al lantului cinematic devine:
![]() (1.4)
(1.4)
unde S - reprezinta numarul de restrictii introduse de legaturile cinematice si se determina cu relatia:
![]() (1.5)
(1.5)
unde: m - reprezinta numarul de restrictii introduse de cuplele cinematice de clasa m;
![]() - reprezinta
numarul de cuple de clasa m,
- reprezinta
numarul de cuple de clasa m,
prin urmare relatia (1.3) devine:
![]() (1.6)
(1.6)
Tinand seama ca unul dintre elemente este fix si ca desi prin ipoteza se inlatura din lant 6 grade de libertate, formula (1.6) devine:
![]() (1.7)
(1.7)
unde ![]() reprezinta
numarul elementelor mobile.
reprezinta
numarul elementelor mobile.
Dobrovolski, a analizat relatia (1.7) si a ajuns la concluzia ca nu are valabilitate generala, deoarece cuplele cinematice se interinfluenteaza. De exemplu se considera mecanismele din fig. 1.24 si fig. 1.25.
Din analiza celor doua mecanisme, se
observa ca daca la un patrulater articular(fig.1.24),
articulatia din C (![]() ) este inlocuita cu o articulatie sferica
) este inlocuita cu o articulatie sferica ![]() (
(![]() ), miscarea tuturor elementelor a ramas
neschimbata(fig1.25).
), miscarea tuturor elementelor a ramas
neschimbata(fig1.25).
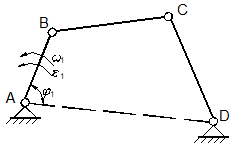
Fig.1.24.
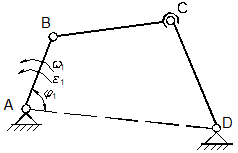
Fig.1.25
Miscarea relativa spatiala dintre elementele 2 si 3, care ar fi posibila din cauza articulatiei sferice, nu este posibila totusi din cauza celorlalte cuple cinematice care determina pentru toate elementele o miscare plana.
In relatia
de mai sus, rezultatul s-ar modifica in cazul mecanismului din fig. 1.25,
datorita cuplei sferice din C (![]() ), in sensul aratat, fara ca miscarea
fizica a lantului sa fie modificata.
), in sensul aratat, fara ca miscarea
fizica a lantului sa fie modificata.
Aceasta interinfluenta, de la distanta, dintre cuplele cinematice, este luata in consideratie in calculul gradului de mobilitate al unui mecanism. Pentru aceasta s-a introdus notiunea de conditie comuna de legatura.
Conditiile comune de legatura, pentru toate elementele lantului cinematic, reprezinta numarul de legaturi, de acelasi tip, impuse tuturor elementelor sale.
Numarul conditiilor comune de legatura se noteaza cu f reprezentand familia mecanismului (lantului) respectiv.
Prin urmare, familia ( f ), reprezinta numarul de restrictii comune tuturor elementelor cinematice, introduse de legaturi.
Familia se determina prin metoda tabelara, cand se analizeaza miscarea fiecarui element in stransa legatura cu miscarea elementelor vecine.
Interinfluenta mentionata mai sus, este luata in consideratie daca se scade numarul conditiilor comune de legatura atat din gradele de libertate ale elementelor libere cat si din conditiile de legatura introduse de cuplele cinematice.
Astfel, Dobrovolski a dat, in final, formula pentru calculul gradului de mobilitate M al unui mecanism:
![]() (1.8)
(1.8)
Pentru
mecanismul plan din fig. 1.24., ![]() , dupa metoda tabelara:
, dupa metoda tabelara:
In consecinta, in cazul foarte frecvent, al mecanismelor plane, din insasi definitia miscarii plan paralele, rezulta ca nici unul dintre elementele lantului nu se poate roti in jurul nici uneia din cele doua axe Ox si Oy ce definesc planul, si nici nu se pot deplasa in translatie dupa axa Oz ce este perpendiculara pe plan. Relatia (1.7) devine:
![]() (1.9)
(1.9)
adica in final:
![]() (1.10)
(1.10)
efectuand calculele:
![]()
Prin urmare, un mecanism este caracterizat de gradul de mobilitate M si de familia f.
Tab. 1.1.
![]()
![]()
![]()
![]()
![]()
![]()
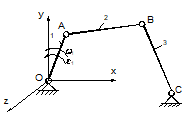
1
2
3
![]()
f = 3
Gradul de mobilitate, reprezinta, din punct de vedere cinematic, numarul parametrilor cinematici independenti care determina miscarea tuturor elementelor.
Din punct de vedere fizic, gradul de mobilitate M, indica numarul elementelor conducatoare sau motoare.
Generalizand, daca se noteaza cu N, numarul de parametrii conducatori ai lantului cinematic rezulta ca daca:
a.
![]() - lantul este
determinat (daca este si inchis, vezi paragraful anterior), este un
mecanism, fig. 1.19.
- lantul este
determinat (daca este si inchis, vezi paragraful anterior), este un
mecanism, fig. 1.19.
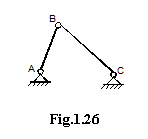
b.
![]() - lantul
cinematic este rigid (uneori este denumit si ferma, fig. 1.26.).
- lantul
cinematic este rigid (uneori este denumit si ferma, fig. 1.26.).
c.
![]() - lant cinematic
nedeterminat (fig. 1.23.)
- lant cinematic
nedeterminat (fig. 1.23.)
Mecanismele se pot clasifica in: plane, spatiale, si in familii si clase.
In studiul sistemelor tehnice, se utilizeaza unele lanturi cinematice particulare, cunoscute sub numele de grupa cinematica sau grupa structurala.
Grupa structurala sau cinematica este un lant cinematic de cea mai simpla forma, caracterizat prin grad de libertate egal cu zero.
Grupa cinematica este caracterizata de clasa, ordin si aspect.
Clasa cea mai mare a grupei gasite in lantul cinematic determina clasa mecanismului.
Clasa grupei este data de rangul maxim al unui element component, daca lantul cinematic care formeaza grupa este deschis, si de numarul de laturi ale conturului poligonal inchis deformabil, daca lantul cinematic al grupei este inchis.
Astfel, vom intalni in practica mecanisme de clasa a II-a, a III-a etc.
Detalii cu privire la caracterizarea grupelor cinematice si o clasificare a mecanismelor plane in clase, in literatura de specialitate. [25];[26];[34];[37].
Cel mai important criteriu de clasificare al mecanismelor, fiind un criteriu general, este clasificarea in familii.
Scopul clasificarii generale a mecanismelor in familii are la baza necesitatea determinarii numarului conditiilor comune de legatura, adica a cifrei f. In acest mod va putea fi calculat gradul de mobilitate al lantului cinematic (relatia 1.7) si deci poate fi cercetata conditia de determinare a lui (de desmodromie). [25];[26];[34];[37];[42];[51];[65];[69].
Un alt scop consta in stabilirea posibilitatilor de decuplare a ecuatiilor necesare pentru determinarea configuratiei, a cinematicii si a cinetostaticii.
Familia se determina prin metoda tabelara asa cum s-a mentionat.
De
exemplu, daca se vor analiza mecanismele din figurile: 1.27; 1.28; 1.29;
1.30; 1.31, mecanismele se pot clasifica in: mecanisme de familia 0 (![]() ); mecanisme de familia 1 (
); mecanisme de familia 1 (![]() ); mecanisme de familia 2 (
); mecanisme de familia 2 (![]() ); mecanisme de familia 3 (
); mecanisme de familia 3 (![]() ) si mecanisme de familia 4 (
) si mecanisme de familia 4 (![]() ).
).
Familia 0.
Tab. 1.2.
n
![]()
![]()
![]()
![]()
![]()
![]()
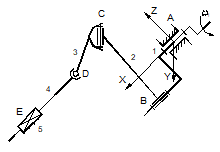
Fig.1.27
1
2
3
4
5
Fig.1.28
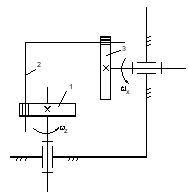
Familia 1.
Tab. 1.3.
n
![]()
![]()
![]()
![]()
![]()
![]()
1
2
3
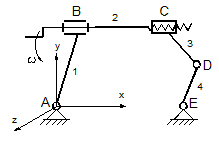 Fig.1.29
Fig.1.29
Familia 2.
Tab. 1.4.
n
![]()
![]()
![]()
![]()
![]()
![]()
1
2
3
4
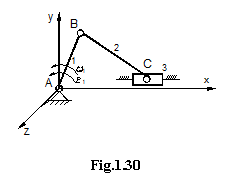 Familia 3.
Familia 3.
Tab. 1.5.
n
![]()
![]()
![]()
![]()
![]()
![]()
1
2
3
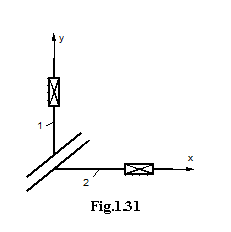
Familia 4.
Tab. 1.6.
n
![]()
![]()
![]()
![]()
![]()
![]()
1
2