Conductivitatea metalelor

Conductivitatea metalelor

In capitolul 1.1. s‑a urmarit procesul conductiei electronice in corpul solid, pe baza modelului zonelor de energie, corespunzator electronilor cvasiliberi cum este cazul la reteaua cristalina a metalelor. S‑a dedus ca in atomii metalului la T = 0 [°K] nivelele de energie permise sunt ocupate pana la o valoare maxima a energiei cores­punzatoare nivelului limita Fermi (W_F). La metale nivelul limita Fermi este totdeauna cuprins intr‑o zona permisa, sau la limita de suprapunere a doua zone permise, la T = 0 [°K].

Sub actiunea campului electric exterior (E_r), cu relatiile stabilite se demon­streaza ca densitatea de durent este:

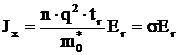(3.1)

similara relatiei clasice (1.12), de unde conductivitatea electrica rezulta:

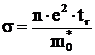(3.2)

care difera de (1.13) prin faptul ca (m) si (t_r) se determina pe baza teoriei cuantice si ca in loc de masa in repaus a electronului intervine masa efectiva.

Conform teoriei clasice, din capitolul (1.1.1), tinand seama ca in metale pur­ta­to­rii de sarcina sunt electronii liberi si deci (q = e), relatia (1.13) devine:

(3.3)

in care (n), (t_r) si (m) au fost precizate in capitolul (1.1.1).

Se constata din (3.2.) ca pe baza teoriei cuantice conductivitatea rezulta ca o cons­tanta de material deoarece depinde de (n) si (n₀). In practica insa se opereaza mai mult rezistivitatea electrica (r = 1/s) ca fiind evident tot constant de material.

S‑a dedus anterior ca odata cu cresterea temperaturii are loc scaderea con­duc­ti­vitatii electrice (relatia 1.16) a metalelor respectiv ca rezistivitatea acestora creste pro­portional cu temperatura.

Daca coeficentul de temperatura al rezistivitatii este:

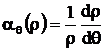(3.4.)

pentru variatia liniara a rezistivitatii cu temperatura, ca in fig. se poate deter­mina rezistivitatea (r_q) la o temperatura oarecare (q) cand este cunoscuta valoarea sa (r₀) la o temperatura (q₀

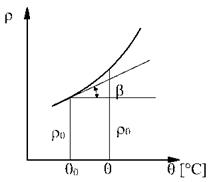
Figura Variatia rezistivitatii cu temperatura.

Din fig. se poate scrie:

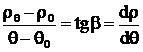(3.5.)

de unde:

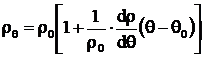(3.6.)

sau inlocuind coeficientul de temperatura al rezistivitatii a₀(R), rezulta:

(3.7.)

La fel se poate calcula si rezistenta electrica folosind in expresia acesteia tot a₀ j) care este constanta de material, si nu a₀(R). De fapt rezistivitatea metalelor va­ria­za liniar cu temperatura numai peste anumite valori ale acesteia numite: tempe­ra­turi Debye (T_D), cum sunt cele prezentate in tabelul pentru cateva elemente.

Tabelul Temperaturi Debye

Sub limitele temperaturilor Debye variatia rezistivitatii cu temperatura este ne­liniara. S‑au facut incercari de exprimare analitica a acestor variatii insa far a se ob­ti­ne rezultate satisfacatoare. Totusi pentru unele aplicatii se poate utiliza expre­sia de forma:

(3.8.)

unde coeficientii se determina pe cale experimentala pentru fiecare material in parte. Daca din (3.8.) se retin numai primii doi termeni se poate deduce o relatie intre coe­fi­cientii de temperatura ai rezstivitatii la temperaturi diferite de forma:

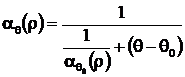(3.9.)

care se utilizeaza fie pentru verificarea coeficientului de temperatura fie pentru deter­minarea sa la temperatura (q) cand este dat la temperatura (q₀

La temperaturi inalte care schimba starea de agregare a metalului, are loc va­riatia brusca a rezistivitatii

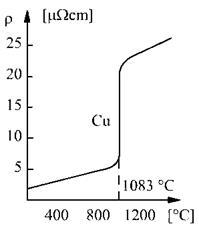
Figura 3.2.Variatia rezistivitatii la schimbarea starii de agregare.

In apropierea temperaturii de topire, pentru cupru se obtine un salt ca cel din fig.3.2., care difera in functie de puritate (grad de aliere).

Ca urmare in siderurgia neferoaselor pentru electrotehnica, variatia rezistivi­ta­tii cu temperatura serveste pentru ajustarea componentelor corespunzator caracteristicilor dorite.

1. FACTORI CARE INFLUENTEAZA REZISTIVITATEA

Din studiul conductibilitatii metalelor a rezultat ca orice nesimetrie a retelei atomice mareste probabilitatea de ciocnire a electronilor cu nodurile retelei, la ace­easi valoare a temperaturii.

Prezenta impuritatilor in reteaua cristalina determina miscarea tim­pu­lui de relaxare, deci a drumului mediu liber parcurs si prin urmare rezistivitatea me­­ta­lu­lui impur este totdeauna mai mare decat daca puritatea ar fi totala. In parti­cular, ali­a­jele prezinta rezistivitati mai mari decat componentele pure din care sunt constituite. In functie de natura compusului (ameste mecanic, solutie solida, com­bi­natie inter­me­talica) rezistivitatea variaza diferit cu proportiile in care se afla com­­ponentele.

Generalizand constatarea experimentala potrivit careia curbele de variatie cu temperatura a rezistivitatiilor a doua (sau mai multor) esantioane ale aceluiasi me­tal avand o impuritate in proportii diferite, sunt echidistante. Matthiessen a atribuit re­zi­stivitatii metalelor doua componente: - una reziduala (r_r) care nu depinde de tem­pe­ratura, ci numai de concentratia impuritatilor; - a doua ideala (r_T) care nu variaza decat cu temperatura. Rezistivitatea totala a metalului cu impuritati se expri­­ma prin relatia lui Matthiessen:

(3.10)

In figura. 3.3 este prezentata variatia cu temperatura a cuprului aliat in diferite proportii cu Nichelul, de unde se deduce confirmarea relatiei (3.10). Prin urmare im­puritatile si agitatia termica afecteaza miscarea electronilor in metal cu timpi dife­riti de relaxare (t_rr) si respectiv (t_rT). Daca se considera ca reteaua cristalina prezinta ne­si­metrii datorate si altor cauze, care determina timpii de relaxare rezistivitatea meta­lu­lui impur, tinand seama de (3.10) si de (3.2.) se poate exprima sub forma:

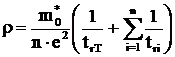(3.11)

Din (3.10) si (3.11) rezulta ca daca prin procedee tehnologice se realizeaza pu­ri­ficarea metalului si deci (r_r = 0), rezistivitatea variaza cu scaderea temperaturii du­pa curba (2) din fig. 3.3, incat la (T = T_c) metalul sufera tranzitia in starea (s.c.). La temperaturi foarte joase (corespunzator ramurii 2) tinand sema de (3.10) si (1.19) rezistivitatea este determinata de relatia:

(3.12)

Daca metalul este impur, la temperaturi foarte joase, rezistivitatea variaza dupa ramura (1) din fig. 3.3 incat la (T = 0) din(3.12) rezulta r r_r

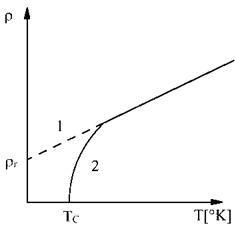
Figura 3.3.Variatia rezistivitatii la temperaturi criogenice.

Din relatia (3.12) rezulta necesitatea purificarii la maxim a metalelor (nealiate) care se utilizeaza la temperaturi foarte scazute.

Influenta tratamentelor mecanice si termice asupra rezistivitatii asupra re­zis­tiviztatii are importanta tehnica  deoarece in timpul uzinarii materialelor conduc­toare acestea isi pot modifica rezistivitatea.

Prin tratamente mecanice (laminare, forjare, trefilare etc.) cu cresterea gra­dului de ecruisaj se realizeaza o deformare mai accentuata a retelei cristaline. Deci un me­tal ecruisat (in starea tare) prezinta o rezistivitate marita deoarece probabilitatea de ciocnire a electronilor cu nodurile retelei este mai mare, functia de unda asociata elec­tronului fiind perturbata in propagarea sa in raport cu o retea cristalina nedefor­ma­ta. De obicei cresterea de rezistanta este de (3-6)%.

Daca insa metalul ecruisat este supus unui tratament termic, deci este readus in starea moale, fara tensiuni interne, se obtine o reducere a gradului de deformare a retelei cristaline si rezistivitatea sa se micsoreaza. Observatii de aceasta natura pot fi facute la masinile electrice bobinate cu bare sau sarme puternic ecruisante, netratate termic, care dupa anumit numar de incalziri si raciri in timpul functionarii, prezinta rezistivitate mai redusa decat in starea noua desi temperaturile realizate nu ating limi­tele de recoacere.

2. MATERIALE SUPRACONDUCTOARE

Proprietatea metalelor de as-i pierde rezistenta electrica la valori scazute ale temperaturii (sub 20 K) a fost descoperita de catre Kamerlingh-Onues in anul 1911, in laboratorul de fizica al universitatii din Leiden (Olanda) cu ocazia experientelor efectuate de el asupra mercurului constatandu-se ca in jurul temperaturii de 4 K rezis­tenta electrica a acestuia devine aproape nula (de circa 10^-5  ).

Fenomenul supraconductibilitatii poate fii inteles imaginandu-ne un conductor metalic in care electronii liberi, sub forma unui gaz electronic se deplaseaza prin re­teaua cristalina a conductorului metalic, in sens opus campului electric aplicat. Im­per­fectiunile retelei perturba miscarea electronilor generand rezistenta electrica a con­duc­torului. In plus, ca orice fluid, gazul electronic este supus agitatiei termice. La temperatura camerei componenta termica a rezistentei e mult mai mare decat com­po­nenta provocata de imperfectiunile retelei cristaline.

Introducand un conductor metalic intr-un gaz lichefiat (in Heliu lichid) la tem­peratura acestuia ( 4,2 K ) rezistenta electrica a conductorului scade brusc. Con­co­mi­tent are loc o considerabila micsorare a rezistivitatii electrice care ajunge pana la va­lori de ordinul 10^-12 *m. Conductorul metalic trece astfel in stare de supra­con­duc­ti­bi­litate, iar temperatura de tranzitie in aceasta stare denumita temperatura critica (Tc) difera de la metal la metal.

Pentru metalele supraconductoare pure, temperatura critica oscileaza intre 0,012 K (wolfram) si 9,22 K (niobiu) iar pentru aliaje intermetalice temperatura cri­ti­ca ajunge la 22,3 K (Nb₃Ge).

Cea mai mare parte a supraconductorilor e formata de aliaje metalice; in anul 1985 se cunosteau peste 1000 de asemenea materiale. Aliajele metalice sunt avan­ta­ja­te, in aplicatiile stintifice si tehnice deoarece poseda temperaturi critice ridicate.

Tabelul 3.2. Temperatura critica si inductia critica a unor metale supraconductoare.

Tabelul 3.3. Temperatura critica si inductia critica a unor compusi supraconductori

Structura retelei materialelor supraconductoare nu se modifica la trecerea lor din starea normala in starea supraconductoare. La trecerea unui metal in starea de supraconductibilitate are loc insa o schimbare in salt, a starii gazului electronic cuan­tic, iar miscarea electronilor in metalul supraconductor este corelata in alt mod decat in metalul normal intrucat la trecerea unui metal in stare supraconductoare ansamblul electronilor de conductie trece simultan intr-o stare noua si intre toti electronii de con­ductie apare o corelare puternica, exista o cauza fizica a acestei corelari si anume interactiunea dintre electroni.

Conform teoriei cuantice a campului electric interactiunea dintre particulele incarcate se realizeaza in urma schimbului dintre ele de catre fotoni: unul dintre elec­troni emite un foton, iar celalalt il absoarbe.

Figura 3.4. Sistemul dinamic al schimbului de fotoni intre cei doi electroni

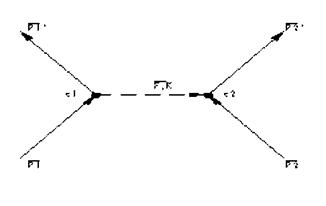
Intre impulsurile electronilor ce participa la schimbul de fotoni, interactiunea dintre cei doi electroni (e₁ si e₂), mediata de fotoni, are un caracter atractiv. Doi astfel de electroni, atragandu-se, formeaza o stare specifica legata, numita 'pereche Cooper'. Evident, intre electronii de conductie actioneaza si forte coulombiene de respingere.Deci formarea perechii Cooper poate avea loc numai in cazul in care atrac­tia dintre cei doi electroni,mediata de fotoni, e mai puternica decat respingerea dintre ei. Pentru ca perechea Cooper sa fie cat mai stabila, energia de atractie trebuie sa fie cat mai mare in valoare absoluta in comparatie cu energia de respingere, fapt ce se realizeaza daca electronii ce formeaza perechile Cooper schimba intre ei fotoni cat mai des.

Se spune ca starea electronilor in perechile Cooper este corelata puternic dupa impulsuri. Aceasta inseamna ca impulsurile electronilor ce formeaza o pereche Cooper nu sunt independente. Ele trebuie sa fie egale in valoare si opuse ca orientare. Dimensiunea unei perechi Cooper este cu mult mai mare decat distanta medie dintre electronii de conductie ( de ordinul 10^-8m) ceea ce inseamna ca intre electronii ce for­meaza o pereche Cooper se gasesc foarte multi alti electroni.

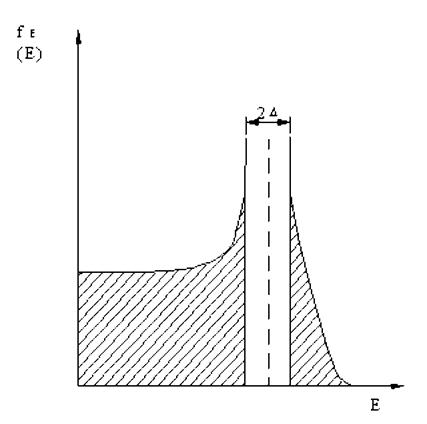
Figura 3.5. Banda de energie interzisa formata in jurul nivelului energetic Fermi

Pentru a desface o pereche Cooper trebuie consumata energie, pentru a invinge fortele de atractie dintre electronii perechi. In principiu exista o probabilitate diferita de zero pentru ca in procesele de interactiune a perechii cu fotonii, aceasta sa pri­meas­ca energia necesara ruperii perechii Cooper. S-ar parea deci ca oscilatiile ter­mi­ce existente la temperatura T<Tc, ar distruge rapid perechile. Totusi perechile Cooper rezista cu succes acestei tendinte, pentru ca la temperatura T<Tc e implicata nu o pe­reche Cooper localizata, nici un sistem de perechi Cooper care nu interac­tio­neaza in­tre ele, ci un colectiv de perechi Cooper care interactioneaza intre ele. In procesele de schimb electronii dintr-o pereche Cooper isi schimba impulsurile astfel incat ei cauta noi parteneri, cu impulsul potrivit, pentru a forma o pereche Cooper cu impulsul total nul (P=0). Deci, in perechea Cooper partenerii se schimba continuu, perechile apar si dispar intr-o constitutie noua. Din acest motiv toti electronii din sistem sunt legati unul cu altul astfel incat atunci cand scoatem din sistem un electron dintr-o pereche Cooper, acesta trebuie rupt nu din perechea lui ci din ansamblul sistemului de perechi in plina interactiune, ceea ce e mult mai dificil.

In cocluzie, in urma interactiunilor electron-foton, la temperatura T<Tc are loc o restructurare a starilor si nivelelor de energie ale electronilor din metal, in urma careia se formeaza starea de supraconductibilitate ce se caracterizeaza printr-o stare energetica excitata, in care un electron este liber si rupt de perechea lui.

Supraconductibilitatea se afla deasupra starii fundamentale a colectivului de perechi Cooper in interactiune si e separata de aceasta printr-un interval finit de ener­gie (banda de energie interzisa) in care nu exista nivele energetice.

Existenta benzii de energie interzise explica disparitia totala a rezistentei elec­trice a metalelor aflate in stare de supraconductibilitate.

In lipsa campului electric toate perechile Cooper au impulsul nul, adica curen­tul electric este nul. Aplicand un camp electric E, cei doi electroni care formeaza pe­rechea Cooper primesc un impuls suplimentar q<>0 ceea ce face ca impulsurile elec­tronilor din pereche sa nu se compenseze reciproc, impulsul total al perechii fiind :

(p+q)+(-p+q)=2q 0 (3.13)

In aceste conditii fiecare pereche se afla in miscare adica intreg colectivul de perechi (de bosoni) se deplaseaza in spatiu ca un intreg, ceea ce reprezinta un curent electric.

Rezistenta electrica apare datorita imprastierii inapoi a electronilor de catre os­cilatiile retelei. Electronii legati in perechi Cooper, nu sunt imprastiati pe defectele retelei sau pe fotoni. intreg colectivul de perechi Cooper, in interactiune, se misca in metalul supraconductor fara ca acesta sa-i opuna rezistenta. Deci rezistenta electrica a supraconductorului e nula.

Odata cu disparitia benzii interuise dispare starea de supraconductibilitate si repare starea normala.

Studiul fenomenului supraconductibilitatii in conformitate cu cele prezentate mai sus, are la baza teoria supraconductivitatii elaborate in anul 1957 de catre John Boredeen, Leon Cooper si Robert Schrieffer, valabila numai pentru materiale supra­conductoare (supraconductori de tipul I).

Trecerea supraconductorilor din stare normala in stare de supraconductoare este reversibila si insotita de modificari ale proprietatilor mecanice, termice si mag­ne­tice ale acestora.

Transformarile mecanice si termice sunt insotite de transformari magnetice, deoarece in interiorul supraconductorului se localizeaza o anumita cantitate de ener­gie mecanica :

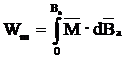(3.14)

M - vectorul magnetizatie ;

B_c - vectorul inductiei magnetice aplicate din interiorul conductorului considerat

Campul magnetic este 'expulzat' din interiorul supraconductorului, prin efect Meissener in mod diferit in diverse materiale. Campul magnetic de tipul I (moi) sunt metale supraconductoare pure, carac­te­rizate printr-o anumita intensitate critica a campului magnetic (Hc) la care, in conditii adecvate de temperatura campul magnetic din interiorul lor dispare brusc, iar ele de­vin diamagnetice. Mai exact in timp ce inductia magnetica B scade la zero in interi­o­rul supraconductoarelor pure, curentul se concentreaza intr-un strat subtire la periferia acestora nemaiputandu-se vorbi de o densitate de curent in sensul clasic al cuvantului. Din acest motiv si pentru-ca intensitatea critica de camp magnetic e rela­tiv mica (H_c) supraconductorii de tipul I au aplicatii foarte reduse.

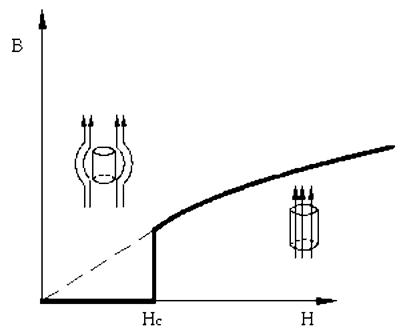
Figura 3.6. Efectul Meissner la supraconductoare moi

Cu totul alta e situatia la supraconductoarele de tipul II sau duri care sunt aliaje metalice binare sau ternare, caracterizate din punct de vedere magnetic prin doua intensitati critice de camp magnetic (Hc₁ si Hc₂). La intensitati mici de camp magne­tic, sub valoarea Hc₁ tranzitia in stare supraconductoare e similara cu cea a supra­con­duc­torilor de tipul I.

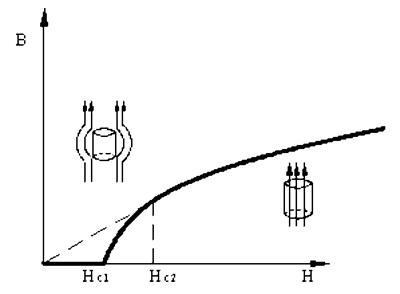
Figura 3.7. Efectul Meissner - supraconductoare dure

Daca intensitatea campului magnetic creste, diamagnetismul se reduce progre­siv, iar la intensitati de camp magnetic H=Hc_2, efectul Meissner este complet. Aceas­ta stare eterogena, care apare intre valorile campurilor magnetice critice Hc₁ si Hc_2, se explica prin existenta unor domenii supraconductoare alternand cu domenii avand conductivitatea normala. Valorile intensitatii campului magnetic Hc₂ sunt ridicate ceea ce e important in aplicatii deoarece prin aceasta se pot obtine densitati mari de curent in supraconductorii de tipul II. In plus temperaturile critice sunt mai ridicate la supraconductorii de tipul II si sunt cuprinse intre 10 K si 21 K.

Supraconductorii de tip II poseda pierderi importante in curent alternativ in special datorate pierderilor prin histerezis. Un alt dezavantaj este efectul de degradare adica intensitatea curentului critic e intotdeauna mai mica la bobinele supracon­duc­toa­re (din supraconductoare lungi) decat la supraconductori scurti. Defectul de de­gra­dare poate fi redus prin cuplarea supraconductorului cu un hiperconductor, hipercon­ductorul fiind un bun conductor de electricitate (Cu, Ag) nu prezinta fenomenul de supraconductibilitate. Rezistenta hiperconductorului scade cu temperatura, dar rama­ne considerabil mai ridicata decat a unui supraconductor veritabil.

Aliajele supraconductoare pe baza de nobiu se obtin prin procedee metalur­gi­ce. Au fost realizate aliaje pe baza de nobiu cu (22-33) % Zr sau cu (55-80) % Ti. De asemenea au fost realizate supraconductoare ternare de tipul Nb-Ti-Zr, Nb-Ta-Ti.  

Dificultatile tehnologice cele mai mari au constat mai ales in alegerea unei teh­nologii optime de laminare si trefilare. In acest sens s-a aplicat o placare prealabila cu Cu a suprafetei supraconductorilor, urmata apoi de laminare si trefilare.

Pe langa aceasta au fost aplicate si alte procedee pentru imbunatatirea tehnolo­giilor de prelucrare :

-folosirea unor tipuri noi de filiere cu protectie de Cu-Ni, care sa permita o fini­sare superioara a suprafetei.

-imbunatatirea regimului termic de recoacere al aliajelor supraconductoare in procesul de trefilare aplicat concomitent pe masini de trefilare cu recoacere continua

-obtinerea supraconductorilor compusi : V₃Si si V₃Si_xC_1-x cu structura A₁₅ sub forma de straturi subtiri, topite in arc, in atmosfera de argon si cu fascicul de elec­troni, in vid, la presiunea de 10^-6 torri

-realizarea aliajelor de tip NB₃Sn di faza de vapori, aplicand evaporarea in vid cu fascicul de electroni prin incalzirea substratului din monocristalul de safir la 750-760 °C la presiunea de 2,7 * 10^-6 torri.

O tendinta actuala in realizarea unor noi tipuri de aliaje supraconductoare o constituie posibilitatea de functionare a supraconductorilor la inductii magnetice mari de 8,5 T si temperaturi de 4,2 K pana la inductii magnetice de 10 T la temperatura de 2,17 K. In campuri magnetice de inductie 5 T densitatea critica de curent este de ordi­nul a 1,5 * 10⁹ A/m².

Pe aceasta baza s-au realizat aliaje de Nb₃Sn, aplicabile in campuri magnetice de inductie 10 T la care aliajele Nb-Ti nu pot functiona.

S-au obtinut de asemenea aliaje de V3Ga cu o mare densitate critica de curent, care desi au temperatura critica T_c=15 K mai mica decat a Nb₃Sn care e de 18 K, totusi pot functiona in campuri magnetice de inductie 12-16 T.

Intrucat realizarea V₃Ga se face la 700 °C iar a Nb₃Sn la 900-1000 °C obti­ne­rea V₃Ga se face cu un grad mai mare de omogenizare.

Aplicatiile supraconductibilitatii in transportul feroviar, in constructia garni­tu­rilor de cale ferata cu perna magnetica permit nu numai marirea vitezei comerciale a trenurilor dar si reducerea substantiala a consumurilor energetice in comparatie cu transportul feroviar conventional.

Tractiunea feroviara pe perna magnetica se face prin actiunea fortelor magneti­ce Lorentz create in sistemul criomagnetic al echipamentului rulant si in calea de ru­lare. Marimea acestor forte se determina cu relatia :

(3.15)

unde, I=intensitatea curentului continuu care circula in infasurarea magnetica a crio­magnetilor ; B=inductia magnetica.

Deplasarea unui tren echipat cu criomagneti supraconductori, in conditii opti­me, impune ca interstitiul dintre criomagneti si calea de rulare sa nu depaseasca 1 cm.

Cercetarile in domeniul aplicarii fenomenului supraconductiei in constructia masinilor electricce de curent continuu si curent alternativ efectuate in SUA, Rusia, Anglia, Germania si Franta au fost orientate catre realizarea unor tipuri de masini electrice de curent continuu heteropolare si homopolare si de masini sincrone utili­za­te in constructia de turbogeneratoare. A fost realizata o gama larga de masini elec­tri­ce de curent continuu heteropolare pentru puteri de 1-10.000 KV in Anglia (firma International Research and Development - IRD) si Germania (firma Siemens). Cerce­tarea stiintifica in acest domeniu e orientata catre realizarea de turbogeneratoare cu mari puteri aparente de peste 10.000 MVA, precum si a unor tipuri specifice de masini sincrone cu infasurari supraconductoare pentru tehnici de varf (tehnica spati­a­la si energetica nucleara).

In electronica, telecomunicatii si tehnica de calcul cercetarea stiintifica a obti­nut rezultate importante prin realizarea si aplicarea jonctiunilor Josephson care si-au gasit un larg camp de aplicatii in realizarea de magnetoetre pentru masuratori in bio­magnetism si geomagnetism; masurarea susceptibilitatii magnetice; masuratori de precizie a tensiunilor electrice de ordinul a 10^-15 V; masuratori tensometrice, efectua­te la temperaturi foarte joase de ordinul a 10^-2-10 K ; producerea de circuite integrate pentru calculatoare electronice cu timp de raspuns de 10^-12 s si puteri consumate foar­te mici de ordinul a 10^-6-10^-9 N ; masuratori de frecvente in domeniul microundelor de ordinul THz in cazul oscilatorilor si detectorilor ; robotica si automatizari indus­tri­ale.

Utilizarea fenomenelor de supraconductie, in aplictiile tehnice, asociata cu cri­za actuala de energie si materii prime a impulsionat intensificarea cercetarilor funda­mentale si aplictive in acest domeniu. S-au efectuat si se dasfasoara in continuare am­ple cercetari pentru aplicarea supraconductorilor in constructia marilor sisteme elec­troenergeticepentru transmiterea fara pierderi sau cu pierderi minime a puterilor elec­trice la valori de peste 700 MVA, pana la 3.000 - 4.000 MVA si de la tensiuni depa­sind tensiunea de 400 KV pentru atingerea unor nivele de 3.000 KV, sisteme racite cu heliu lichid (cabluri electrice, accesorii de cabluri, transformatoare si masini elec­trice).

In diferite tari se fac cercetari privind utilizarea magnetilor supraconductori in: biologie (la cresterea plantelor, pasarilor si animalelor); chimie (pentru conducerea reactiilor chimice si catalitice) ; medicina (pentru vindecarea anevrismelor fara inter­ventii operatorii); fizica Corpului solid, microscopia electronica si studiul ercetarii metalelor, producerea energiei in energetica termonucleara si in instalatiile magne­to­hidrodinamice cu magneti supraconductori; tratarea apelor reziduale, ecranarea si formarea campurilor magnetice cu ajutorul foliilor supraconductoare; in fizica energi­i­lor inalte; accelerarea particulelor elementare prin magneti dipolari si cvadripolari, in campuri magnetice cu inductia de ordinul a T si cu energii de circa 800 MJ.

Deci se poate spune ca supraconductibilitatea are un rol esential in dezvoltarea gradului de tehnologizare, deschizand o noua era in acest domeniu, si merita toata atentia de care se bucura din partea celor mai mari laboaratoare si cercetatori ai lumii.