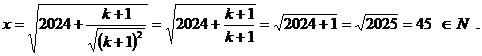Propuneri de subiecte pentru olimpiada de matematica

PROPUNERI DE SUBIECTE PENTRU OLIMPIADA DE MATEMATICA

CLASA A V-A

1.Aratati ca numarul natural y=a+b²⁰⁰⁹+c este patrat perfect unde ,

a= , b=iar c reprezinta ultima cifra a numarului 2²⁰⁰⁹.

2.Aratati ca numarul natural este cub perfect , unde a este ultima cifra a numarului x=2²⁰⁰⁸+6²⁰⁰⁹ iar b este ultima cifra a numarului y=3²⁰⁰⁹+2²⁰¹⁰ .

3.Comparati numerele naturale a=2¹⁰² 5¹⁰⁴ si b=3²²⁴.

4.Comparati numerele naturale a=2¹⁸³ 11¹⁴⁴ si b=3¹²² 5²¹⁶ .

5.Aratati ca numarul natural n=1+3¹+3²+3³+ ..+3⁹⁹ are ultima cifra 0.

6.Aratati ca numarul natural n=1+7¹+7²+7³+ ...+7⁹⁹ are ultimele doua cifre egale cu 0.

7.Aratati ca numarul natural n=(1+3¹+3²+3³+ ..+3⁹⁹) (1+7¹+7²+7³+ ...+7⁹⁹ ) are ultimele trei cifre egale cu 0.

8.Aratati ca pentru orice numar natural n , n 2 numarul x=10ⁿ+32 este divizibil cu 12.

9.Aratati ca numarul natural n= 1+3+5+7+ ..+(2k+1) este patrat perfect oricare ar fi kIN.

10.Aratati ca numarul natural n=1+3+5+7+ ...+2009 este patrat perfect.

CLASA A VI-A

1.Aflati numarul natural x din proportia , unde a= .

2.Aflati numarul natural x din proportia unde a=1+3¹+3²+3³+ ..+3⁹⁹.

3.Aratati ca .

4.Numerele naturale a , b , c si d sunt direct proportionale cu primele patru numere naturale prime si .Aflati numerele.

5.Simplificati fractia ,xIN , pentru a obtine o fractie ireductibila.

6.Rezolvati ecuatia , xIN.

CLASA A VII-A

1.a)Aratati ca nu exista patrate perfecte de forma 4m+3 , unde mIN.

b)Aratati ca numarul x= I R-Q.

2.a)Aratati ca nu exista patrate perfecte de forma 5n+2 unde nIN.

b)Aratati ca numarul x=I R-Q .

3.Determinati numarul natural nenul n astfel incat .

4.Fie numerele reale a₁ , a₂ , .. , a_n astfel incat

Calculati S=a₁+a₂+ ..+a₂₀₀₉ .

CLASA A VII-A SAUA VIII-A

1.Aratati ca numarul x= este numar natural.

2.Aratati ca numarul n= este numar natural oricare ar fi kIN.

3.Aratati ca numarul x= este numar natural oricare ar fi kIN.

Rezolvari:

Clasa a V-a

1.

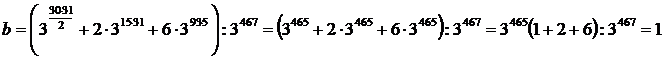
, deci y=118+1²⁰⁰⁹+2=121=11² ,

deci y este patrat perfect.

2.

, deci , deci este cub perfect.

3. facem urmatoarele transformari:

^, si cum 8<9 , 25<27 avand exponentii egali avem a<b.

4. facem urmatoarele transformari:

,

si cum 8<9 , 121<125 avand exponentii egali avem a<b.

5. obs. ca 1+3¹+3²+3³=40 si n este o suma de 100 termeni deci se poate grupa suma in grupe de cate 4 termeni. Scriem suma astfel:

n=1+3¹+3²+3³+ ..+3⁹⁹ = (1+3¹+3²+3³)+3⁴(1+3¹+3²+3³)+ ..+3⁹⁶(1+3¹+3²+3³) =

= 40+3⁴ 40+.+3⁹⁶ 40 = 40(1+3⁴+...+3⁹⁶) T10 / n T ultima cifra a lui n este 0.

6.obs. ca 1+7¹+7²+7³=400 si n este o suma de 100 termeni care pot fi grupati in grupe de cate 4 termeni. Scriem suma astfel:

n=1+7¹+7²+7³+ ...+7⁹⁹=(1+7¹+7²+7³)+7⁴ (1+7¹+7²+7³)+ ...+7⁹⁶(1+7¹+7²+7³)=

= 400+7⁴ 400+ ...+7⁹⁶ 400 = 400(1+7⁴+ ..+7⁹⁶) T 100 / n T ultimele doua cifre ale lui n sunt egale cu 0.

7.din ex. 6 si 7 avem ca u(1+3¹+3²+3³+ ..+3⁹⁹ )=0 si ultimele doua cifre ale sumei

1+7¹+7²+7³+ ...+7⁹⁹ sunt egale cu 0 de unde avem ca ultimele trei cifre ale produsului

(1+3¹+3²+3³+ ..+3⁹⁹ ) (1+7¹+7²+7³+ ...+7⁹⁹) sunt egale cu 0.

8. Suma cifrelor numarului x=10ⁿ+32 este egala cu 6 (1+3+2) , oricare ar fi n numar natural , deci 3 / x.

pentru n 2 ultimele cifre ale lui x vor fi 3 si 2 ; cum 4 / 32 avem ca 4/x .

cum 3 si 4 sunt prime intre ele si 3 4=12 avem ca 12 / x.

9. n= 1+3+5+7+ ..+(2k+1) = 1+2+3+4+5+....+(2k+1) - (2+4+6+ ...+2k)=S₁-S₂.

S₁=(2k+1)(2k+2):2 = (2k+1)(k+1) , S₂=2(1+2+3+.+k)=2k(k+1):2= k(k+1) ,

Deci , n=(2k+1)(k+1) - k(k+1)= (k+1)(2k+1-k)=(k+1)(k+1)=(k+1)²

10.ca un caz particular al ex. 9 avem 1+3+5+7+ ...+2009=1004².

Clasa a VI-a

1. Obs. ca deci , . Asemanator pentru celelalte fractii.

Cu acest rezultat avem:

a= =

Cu acest rezultat scriem proportia astfel:

.

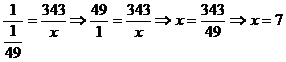2. a=1+3¹+3²+3³+ ..+3⁹⁹ T 3a=3¹+3²+3³+ ..+3⁹⁹+3¹⁰⁰

T 3a-a = 3¹⁰⁰- 1 T2a=3¹⁰⁰- 1T a= . Cu acest rezultat scriem proportia:

.

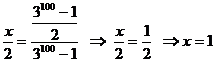3.Aducem la acelasi numitor suma de fractii amplificand corespunzator si obtinem:

.

Fie S=1+2¹+2²+ ..+2⁹⁹ T 2S=2+2²+ .. +2¹⁰⁰ , T 2S-S=2¹⁰⁰-1 de unde S=2¹⁰⁰-1.

Cu aceasta obtinem:

deorece 2¹⁰⁰-1<2¹⁰⁰ .

4. a=2k , b=3k , c=5k , d=7k, k numar natural , de unde:

Cu acest rezultat avem: a=10 , b=15 , c=25 , d=35.

5. .

6. .

CLASAA VII-A

1.a)Orice numar natural are una din formele 4k , 4k+1 , 4k+2 sau 4k+3 , deci orice patrat perfect are una din formele : (4k)² , (4k+1)² , (4k+2)² sau (4k+3)².

(4k)²=16k² deci este de forma 4m;

(4k+1)²=16k²+8k+1 , deci este de forma 4m+1;

(4k+2)²=16k²+16k+4 , deci este de forma 4m;

(4k+3)²=16k²+24k+9 , deci este de forma 4m+1.

De mai sus rezulta ca nu exista patrate perfecte de forma 4m+3.

b) x== , cum nu exista p.p. de forma 4m+3 avem ca xIR-Q.

2.a) u(5n) I Tu(5n+2) I T 5n+2 nu este patrat perfect oricare ar fi numarul natural n ;

b)x= ,

deci , si cum nu exista numere naturale de forma 5n+2 care sa fie p.p. avem ca xIR-Q.

3.Obs. ca .Asemanator avem si pentru celelalte rapoarte. Cu acest rezultat avem:

.

Cu acest rezultat egalitatea din enunt devine:

4.Inegalitatea din enunt devine:

S=1+2+3+ ..+2009=.

CLASA A VIII-A

1. .Astfel avem:

x==

. In continuare avem:

x=

2.Fien= 1+3+5+7+ ..+(2k+1)

n= 1+3+5+7+ ..+(2k+1) = 1+2+3+4+5+....+(2k+1) - (2+4+6+ ...+2k)=S₁-S₂.

S₁=(2k+1)(2k+2):2 = (2k+1)(k+1) , S₂=2(1+2+3+.+k)=2k(k+1):2= k(k+1) ,

Deci , n=(2k+1)(k+1) - k(k+1)= (k+1)(2k+1-k)=(k+1)(k+1)=(k+1)²

Asadar , 1+3+5+7+..+(2k+1)=(k+1)² .

3.Folosind rezultatul de la ex.2. , 1+3+5+7+..+(2k+1)=(k+1)²avem: