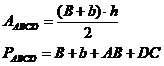|
|
|
PATRULATER CONVEX
Def: Un patrulater se numeste convex daca oricare ar fi o latura a sa, cele doua varfuri nesituate pe latura considerata, se afla de aceeasi parte a dreptei in care este inclusa latura respectiva.
Proprietate: Suma masurilor unghiurilor unui patrulater convex este egala cu 3600.
PARALELOGRAMUL
Def: Paralelogramul este patrulaterul convex cu laturile opuse
paralele doua cate doua.
Proprietati:
intr-un paralelogram laturile opuse sunt congruente doua cate doua;
intr-un paralelogram laturile opuse sunt congruente si paralele;
intr-un paralelogram unghiurile opuse sunt congruente doua cate doua;
intr-un paralelogram oricare doua unghiurile alaturate sunt suplementare;
intr-un paralelogram diagonalele se impart in parti congruente.
Reciproca:
Un patrulater convex este paralelogram daca:
laturile opuse sunt congruente doua cate doua;
doua laturi opuse sunt paralele si congruente;
unghiurile opuse sunt congruente doua cate doua;
oricare doua unghiuri alaturate sunt suplementare;
diagonalele se impart in parti congruente.
Perimetrul si aria :
DREPTUNGHIUL
Def: Dreptunghiul este paralelogramul cu un unghi drept.
Proprietati
are toate proprietatile unui paralelogram;
are toate unghiurile congruente - drepte;
intr-un dreptunghi diagonalele sunt congruente.
Reciproca:
Un patrulater convex este dreptunghi daca:
are toate unghiurile congruente;
are trei unghiuri drepte;
este paralelogram si are un unghi drept;
este paralelogram si are diagonalele congruente.
Perimetrul si aria :
ROMBUL
Def: Rombul este paralelogramul cu doua laturi consecutive congruente.
Proprietati:
are toate proprietatile unui paralelogram;
are toate laturile congruente;
are diagonalele perpendiculare;
are diagonalele bisectoarele pentru unghiurilor sale.
Reciproca:
Un patrulater convex este romb daca:
are toate laturile congruente;
este paralelogram si are doua laturi consecutive congruente;
este paralelogram si are diagonalele perpendiculare;
este paralelogram si o diagonala este bisectoare pentru unul din unghiurile sale.
Perimetrul si aria :
PATRATUL
Def: Patratul este dreptunghiul cu doua laturi consecutibe congruente.
Def: Patratul este rombul cu un unghi drept.
Proprietati:
are toate proprietatiile paralelogramului,
are toate proprietatiile dreptunghiului;
are toate proprietatiile rombului.
Reciproca:
Un patrulater convex este patrat daca:
este dreptunghi si are doua laturi consecutive congruente;
este dreptunghi si are diagonalele perpendiculare;
este dreptunghi si are diagonalele bisectoare pentru unghiurile din care pornesc;
este romb si are un unghi drept;
este romb si are diagonalele congruente.
Perimetrul si aria :
TRAPEZUL
Def: Trapezul este patrulaterul convex in care doua laturi
opuse si numai ele sunt paralele. Laturile paralele se numesc bazele trapezului
(baza mare, respective baza mica)
Clasificare
oarecare;
dreptunghic (are un unghi de 900);
isoscel (laturile neparalele congruente).
Linia mijlocie:
Def: Segmentul care uneste mijloacele laturilor neparalele ale unui trapez se numeste linie mijlocie a trapezului.
Linia mijlocie a trapezului trece prin mijloacele diagonalelor trapezului.
Linia mijlocie a trapezului este paralela cu bazele trapezului.
Linia
mijlocie a trapezului are lungimea cat semisuma lungimilor bazelor:
Segmental determinat de
mijloacele diagonalelor trapezului are lungimea cat semidiferenta lungimilor
bazelor trapezului.
Proprietatile trapezului isoscel
are laturile neparalele congruente;
are unghiurile alaturate bazelor respectiv congruente;
are diagonalele congruente;
diagonalele formeaza cu bazele triunghiuri isoscele;
daca se prelungesc laturile neparalele acestea formeaza cu bazele doua triunghiuri isoscele.
Reciproca:
Un patrulater convex este trapez isoscel daca:
are doua laturi paralele si necongruente, iar celelalte doua laturi sunt congruente;
este trapez si are unghiurile alaturate unei baze, congruente;
este trapez si are diagonalele congruente;
s-a obtinut prin construirea unei paralele la baza unui triunghi isoscel.
Perimetrul si aria :
