
|
|
|
Extreme locale ale functiilor de mai multe variabile reale
Definitia1
Fie A o
submultime din Rn si f:A![]() R.
R.
I. Spunem ca punctul a![]() este un punct de minim absolut pentru funtia f daca
este un punct de minim absolut pentru funtia f daca
f(a)≤f(x), ![]()
II. Spunem ca punctual a![]() este un punct de maxim absolute pentru functia f daca
este un punct de maxim absolute pentru functia f daca
f(a)≥f(x), ![]()
numarul f(a)=inf se numeste valoare minima a fucntiei f pe A iar
f(a)=supse numeste valoare maxima a functiei f pe A.
Observatie!
Remarcam ca nu intotdeauna exista pentru o functie data puncte de minim sau de maxim absolute.Am vazut insa ca daca f este o functie continua pe un compact cu valori reale, atunci asemenea puncte exista.
Definitia2
Fie A![]() Rn si f:A
Rn si f:A![]() R.
R.
I.Un punct a![]() spunem ca este punct de minim local
sau minim relative pentru funatia f daca exista o vecinatate V a punctului a
a.i.
spunem ca este punct de minim local
sau minim relative pentru funatia f daca exista o vecinatate V a punctului a
a.i.
(1) f(a)≤f(x), pentru ![]() .
.
II. Un punct a![]() spunem ca este punct de maxim local
sau maxim relative pentru f daca exista o vecinatate V a punctului a a.i.
spunem ca este punct de maxim local
sau maxim relative pentru f daca exista o vecinatate V a punctului a a.i.
(2)f(a)≥f(x),
pentru ![]() .
.
Punctele de maxim sau de minim local se numesc puncte de extrem local sau de extrem relativ.
Se observa, din definitia de mai sus, ca un punct
a este punct de extreme local daca
exista o vecinatate V a punctului a
a.i. diferenta f(x)-f(a) sa pastreze semn constant pe V![]() A.
A.
Definitia3
Fie D un
deschis din Rn si f:D![]() R.Spunem ca un punct a
R.Spunem ca un punct a![]() este punct stationar sau punct
critic pentru functia f daca f este
diferentiabila in a si df(a)=0.
este punct stationar sau punct
critic pentru functia f daca f este
diferentiabila in a si df(a)=0.
Teorema1 (teorema lui Fermat)
Fie D un deschis din Rn.
Daca functia f:D![]() R este diferentiabila intr-un punct a
R este diferentiabila intr-un punct a![]() care este in acelasi timp punct de
extreme local pentru f, atunci df(a)=0, adica a este punct critic.
care este in acelasi timp punct de
extreme local pentru f, atunci df(a)=0, adica a este punct critic.
Dem.
Fie v un
versor arbitrar din Rn.Intrucat a este punct extreme local al
funcitei f,exista o sfera deschisa S(a,r)![]() D pe care diferenta f(x)-f(a)
pastreaza semn constant.Fie functia
D pe care diferenta f(x)-f(a)
pastreaza semn constant.Fie functia ![]() definite prin
definite prin
![]() f(a+tv),
f(a+tv), ![]()
Cum a este punct extreme local, diferenta ![]() f(a+tv)-f(a) pastreaza semn constant
pentru t
f(a+tv)-f(a) pastreaza semn constant
pentru t![]() , de unde rezulta ca t=0 este punct
de extreme local pentru
, de unde rezulta ca t=0 este punct
de extreme local pentru ![]()
Conform teoremei lui Fermat pentru functii de o
variabila reala (teorema 2.2.), rezulta ca ![]() . Dar, aceasta antreneaza
. Dar, aceasta antreneaza ![]()
In
particular, considerand V unul din versorii bazei canonice (ek) , k=![]() obtinem ca
obtinem ca ![]() , ceea ce contrazice ca df(a)=
, ceea ce contrazice ca df(a)=![]()
Observatie!
Teorema lui Fremat afirma ca punctele de extreme local ale unei fucntii diferentiabile se gasesc printer punctele sale critice.Deci, conditia ca diferentiala sa se anuleze intr-un punct este necesara nu insa si suficienta pentru ca punctual sa fie de extreme local.In acest sens sa analizam
Ex1.
Fie
functia f:R2![]() R definite prin f(x,y)=x2-y2.Atunci
R definite prin f(x,y)=x2-y2.Atunci ![]()
![]() ; deci df(0,0)=0. Dar punctul (0,0)
nu eset nici punct de maxim si nici de
minim local intrucat ne exista nici o sfera deschisa cu centrul in (0,0) pe
care diferenta f(x,y)-f(0,0)=x2-y2 sa pastreze semn
constant.
; deci df(0,0)=0. Dar punctul (0,0)
nu eset nici punct de maxim si nici de
minim local intrucat ne exista nici o sfera deschisa cu centrul in (0,0) pe
care diferenta f(x,y)-f(0,0)=x2-y2 sa pastreze semn
constant.
Mia mult, seobserva ca functia g(x)=f(x,0)=x2 are minim in 0 iar functia h(y)=f(0,y)=-y2 are maxim in 0.(vezi figura de mai jos)
Definitia4
Un punct stationar care nu este punct de extreme se numeste punct sa.
Desen
Teorema2
Fie D un
deschis din Rn si f:D![]() R o functie de clasa C2 pe
D. Daca a
R o functie de clasa C2 pe
D. Daca a![]() este un punct de minim local pentru
f, atunci
este un punct de minim local pentru
f, atunci
(3)d2f(a)≥0.
Dem.
Cum f ![]() C2(D), putem sa aplicam
formula lui Taylor cu q=2. Prin urmare, pentru orice x
C2(D), putem sa aplicam
formula lui Taylor cu q=2. Prin urmare, pentru orice x![]() S(a,r)
S(a,r)![]() exista un punct
exista un punct ![]() [a,x] a.i.
[a,x] a.i.
f(x)=f(a)+![]()
Conform teoremei lui Fermat, df(a)=0 si atunci, din relatia precedenta , obtinem
f(x)-f(a)= ![]()
de unde adunand si scazand d2f(a)(x-a) gasim
f(x)-f(a)=![]() , pentru
, pentru ![]()
Cum f este punct de minim rezulta ca
f(x)-f(a)≥0,
![]()
Daca x-a=h, atunci din ultimele doua relatii avem
(4) f(a+h)-f(a)= ![]() ≥0, pentru ||h||<r.
≥0, pentru ||h||<r.
Fie acum x![]() Rn cu x≠0 si fie t
Rn cu x≠0 si fie t![]() a.i.
a.i.
||tx||<r, adica |t|<![]()
Atunci,aplicand (4) pentru h=tx si tinand seama
ca ![]() depinde de t, obtinem:
depinde de t, obtinem:
![]() ≥0, pentru orice t cu |t|<
≥0, pentru orice t cu |t|<![]() , de unde
, de unde
![]() ≥0,
≥0, ![]() |t|<
|t|<![]()
sau
![]() ≥0,
≥0, ![]() |t|<
|t|<![]()
Facand t![]() 0 in ultima relatie si tinand seama
ca
0 in ultima relatie si tinand seama
ca ![]() iar d2f este continua in a, rezulta
ca
iar d2f este continua in a, rezulta
ca
d2f(a)(x)≥0, ![]() Rn, cu care teorema este
complet demonstrate.
Rn, cu care teorema este
complet demonstrate.
Observatii!
Un
rezultata analog are loc daca a este
un punct de maxim local.Mai précis, daca f![]() C2(D), unde D este un
deschis din Rn, si a
C2(D), unde D este un
deschis din Rn, si a![]() este un punct de maxim local pentru
f, atunci d2f(a)≤0.
este un punct de maxim local pentru
f, atunci d2f(a)≤0.
Ca si pentru functiile de o variabila reala se pune problema gasirii unor conditii suficiente pentru ca un punct stationar sa fie punct de extreme.In acest scop vom stabili, mai intai,o lema:
Lama1
Fie [![]() ]1≤i,j≤n o
matrice simetrica de numere reale (
]1≤i,j≤n o
matrice simetrica de numere reale (![]()
![]() , pentru
, pentru ![]() ) si fie
) si fie ![]() forma patratica asociata.Daca
forma patratica asociata.Daca ![]() este pozitiv definite, adica
este pozitiv definite, adica ![]() >0 pentru orice x
>0 pentru orice x![]() Rn|, atunci exista o
constanta m>0 a.i.
Rn|, atunci exista o
constanta m>0 a.i.
(5) ![]() ≥m||x||2,
≥m||x||2, ![]() Rn .
Rn .
Dem.
Fie C=.Se ve de ca
multimea C este marginita si inchisa, deci compacta.Cum ![]() este o functie continua pe compavtul C, exista
un punct x0
este o functie continua pe compavtul C, exista
un punct x0![]() in care functia
in care functia ![]() isi atinge minimul absolute.Deci, daca m=inf, atunci
isi atinge minimul absolute.Deci, daca m=inf, atunci ![]() .Intucat x0
.Intucat x0![]() rezulta ca x0≠0, si
rezulta ca x0≠0, si ![]() , fiind pozitiv definita, obtinem ca
m=
, fiind pozitiv definita, obtinem ca
m=![]() , iar pentru orice y
, iar pentru orice y![]() are loc
are loc ![]()
Observam ca (5) este verifivata pentru x=0.
Sa
presupunem ca x![]() Rn|.Fie y=
Rn|.Fie y=![]()
Evident y![]() si deci
si deci ![]() de unde
de unde ![]() ||x||2, adica (5) este
verificata si de punctele x
||x||2, adica (5) este
verificata si de punctele x![]() Rn cu x≠0. In
concluzie, (5) are loc pentru orice x
Rn cu x≠0. In
concluzie, (5) are loc pentru orice x![]() Rn.
Rn.
Teorema3
Fie f o functie de clasa C2 pe deschisul D din Rn si a un punct critic pentru f.Daca forma patratica d2f(a) este:
1. pozitiv definite, atunci a este punct de minim local;
2. negative definite (adica - d2f(a) este pozitiv definita), atunci a este punct de maxim local.
Dem.
1. Sa presupunem , mai intai, ca forma patratica d2f(a) este pozitiv definite.Am vazut in cap11.5 ca in acest caz matricea asociata
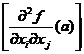 este simetrica.
este simetrica.
Aplicand teorema2 formai patratice d2f(a) rezulta ca exista m>0 a.i.
(6) d2f(a)(x-a)≥m||x-a||2, pentru ![]()
Pe
de alta parte, cum f![]() C2(D) putem sa aplicam formula lui Taylor cu
q=2.Prin urmare, pentru orice x
C2(D) putem sa aplicam formula lui Taylor cu
q=2.Prin urmare, pentru orice x![]() S(a,r)
S(a,r)![]() D exista un punct
D exista un punct ![]() [a,x] a.i.
[a,x] a.i.
f(x)=f(a)+ ![]()
Deoarece a este un punct stationar, avem df(a)(x-a)=0 si atunci din relatia precedenta obtinem
(7) f(x)-f(a)= ![]()
=![]()
de unde , adunand si scazand d2f(a)(x-a), gasim
(7') f(x)-f(a)= ![]()
Dar f este de clasa C2 pe D si atunci,
derivatele partiale de ordin doi fiind continue, paranteza se poate scrie sub
forma ![]() ||x-a||2, unde
||x-a||2, unde ![]() .Utilizand relatiile (6) si (7'),
avem mai departe
.Utilizand relatiile (6) si (7'),
avem mai departe
f(x)-f(a)≥![]() ||x-a||2+
||x-a||2+![]() ||x-a||2=
||x-a||2=![]()
![]()
Cum m>0 si ![]() , putem gasi un r1>0
a.i.
, putem gasi un r1>0
a.i.
m+![]() , pentru
, pentru ![]()
Deci f(x)-f(a)≥0 pentru ![]() , ceea ce spune ca a este punct de minim local.
, ceea ce spune ca a este punct de minim local.
2. Daca d2f(a) este negative definite, se aplica rezultatul de la punctual 1 functiei -f, de unde se obtine imediat afirmatia teoremei, punctul 2.
Teorema4
Fie D un
deschis in R2, f![]() C2(D) si a un punct critic pentru f.
C2(D) si a un punct critic pentru f.
Sa notam prin A=![]() B=
B=![]() C=
C=![]() Daca :
Daca :
1. B2-AC<0 si A>0 , atunci a este punct de minim local;
2. B2-AC<0 si A<0, atunci a este punct de maxim local;
3. B2-AC>0, atunci a nu este punct de extreme.
Dem.
Fie a=(a1,a2) si (x,y) un punct generic din D. Observam ca
d2f(a)(x-a1,y-a2)=(x-a1)
![]() +(y-a2)2
+(y-a2)2 ![]()
Presupunand, fara a micsora generalitatea, ca y≠a2 , avem
d2f(a)(x-a1,y-a2)=![]()
Daca notam cu u=![]() , atunci se observa ca d2f(a)
are semn constant daca si numai daca trinomul Au2+2Bu+C are radacini
cpmplexe, adica daca B2-AC<0.
, atunci se observa ca d2f(a)
are semn constant daca si numai daca trinomul Au2+2Bu+C are radacini
cpmplexe, adica daca B2-AC<0.
In acest caz, semnul sau este dat de semnul lui A.
Prin urmare, d2f(a) va fi pozitiv definite daca A>0 si negative definite daca A<0.Conform teoremei precedente, pentru A>0 punctul a este punct de minim local (punctual 1 al teoremei noastre) , iar pentru A<0, punctual a este punct de maxim local (puctul 2 al teoremei).
3. Daca B2-AC>0, atunci d2f(a) nu mai pastreaza semn constant si atunci, nici diferenta f(x,y)-f(a1,a2) nu mai pastreaza semn constant pe nici o vecinatate a punctului a, ceea ce spunce ca a nu este punct de extreme.
Observatie!
Daca B2-AC=0, nun e putem pronunta daca punctul a este sau nu punct de extreme.In acest caz, semnul diferentei f(x,y)-f(a1,a2) depinde de semnul diferentialelor lui f de ordin superior.
Ex2.
Sa se
determine punctele de extreme local ale functiei f:R2![]() R, definita prin
R, definita prin
f(x,y)=x4+y4+2x2y2-8x+8y.
Observam ca ![]() 4x3+4xy2-8,
4x3+4xy2-8,![]() 4y3+4x2y+8.
4y3+4x2y+8.
Rezolvand sistemul format din ecuatiile ![]()
![]() , se obtine solutia x=-1, y=1.
, se obtine solutia x=-1, y=1.
Prin urmare, punctual a=(-1,1) este punct stationar.
Pentru a vedea daca a este punct de extreme sa calculam si derivatele partiale de ordin
2, ![]() 12x2+4y2,
12x2+4y2, ![]() 12y2+4x2,
12y2+4x2, ![]() 8xy,
8xy,
de unde
A=![]() 16,B=
16,B=![]() -8, C=
-8, C=![]() 16.
16.
Prin urmare, B2-AC=64-162<0 si cum A>0 rezulta ca a este punct de minim.
In cazul functiilor de mai multe variabile reale, tinand seama de conditiile lui Sylvester din teoria formelor patratice([13]), pentru a putea vedea daca forma patratica d2f(a) este pozitiv sau negative definite se poate utilize urmatorul criteriu:
Teorema5
In ipotezele lemei 1 daca:
1. toate numerele
![]() ,
, 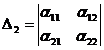 ,..,
,.., ,
,
unde 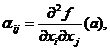 sunt strict positive,
atunci forma patratica d2f(a) este pozitiv definite in a este punct de minim local;
sunt strict positive,
atunci forma patratica d2f(a) este pozitiv definite in a este punct de minim local;
2. toate numerele
-![]() ,
,![]() .,(-1)n
.,(-1)n![]() sunt strict positive,
sunt strict positive,
Atunci forma patratica d2f(a) este negative definite si a este punct de maxi local.
(
![]() ,
,![]() .,
.,![]() sunt minorii
principali ai matricei hessiene [
sunt minorii
principali ai matricei hessiene [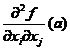 ] ).
] ).
Dem.
Demonstratia
teoremei este o consecinta imediata a irmatorului rezultat algebric(conditiile
lui Sylvester): Fie ![]() o forma patratica a
carei matrice asociata [
o forma patratica a
carei matrice asociata [![]() ]1≤i,j≤n este simetrica. Daca:
]1≤i,j≤n este simetrica. Daca:
a) minorii principali ai matricei, adica
![]() ,
, 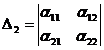 ,..,
,..,  ,
,
Sunt
pozitivi,atunci ![]() este pozitiv definite;
este pozitiv definite;
b)-![]() ,
,![]() .,(-1)n
.,(-1)n![]() sunt pozitivi, atunci
sunt pozitivi, atunci ![]() este negative
definite.
este negative
definite.
Ex3.
Fie
functia f:R3![]() R definita prin
R definita prin
f(x,y,z)=x2+3y2+2z2-2xy+2xz.
Avem ![]() 2x-2y+2z,
2x-2y+2z, ![]() 6y-2z,
6y-2z,![]() 4z+2x.
4z+2x.
Rezolvand
sistemul ![]() 0,
0, ![]() 0,
0, ![]() 0 gasim a=(0,0,0) punct critic al functiei f.
0 gasim a=(0,0,0) punct critic al functiei f.
Pentru a vedea daca a este punct de extreme, sa calculam derivatele partiale de ordin 2. Avem:
![]() 2,
2,![]() 6,
6,![]() 4,
4,
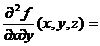 -2,
-2, 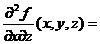 2,
2, 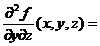 0,
0,
De unde matricea hessiana devine
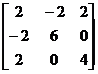
Observam ca ![]()
![]() iar
iar ![]() , ceea ce spune ca forma patratica d2f(0,0,0)
este pozitiv definite si deci a este
punct de minim local al functiei f, conform teoremei 5.
, ceea ce spune ca forma patratica d2f(0,0,0)
este pozitiv definite si deci a este
punct de minim local al functiei f, conform teoremei 5.