Diferentiala functiilor compuse

Diferentiala functiilor compuse

Teorema13(Legea lantului)

Fie F:D, D =o multime deschisa din Rⁿ si

=o multime deschisa din R^m

G:R^p (n≥1,m≥1,p≥1 ).

Daca F-diferentiabila in aD si G-diferentiabila in b=F(a), atunci GF:DR^p este diferentiabila in a si

(1)     d(GF)(a)=dG(F(a))dF(a).

dem.

F-diferentiabila in punctual aD () operator liniar T=df(a):RⁿR^m si o functie R^m a.i. (2)F(x)=F(a)+T(x-a)+(x)||x-a||, xD, unde .

G-diferentiabila in b=F(a) ()operator liniar S=dG(b):R^mR^p si a unei functii R^p a.i. (3) G(y)=G(b)+S(y-b)+(y)||y-b||, y , unde

Pentru fiecare xD, fie y=F(x).Inlocuind in relatia (3) y-b cu F(x)-F(a) si tinand seama de (2) obtinem:

(4) G(F(x))=G(F(a))+S(F(x)-F(a))+(F(x))||F(x)-F(a)||, xD de unde avem:

GF(x)=GF(a)+S(T(x-a)+(x)||x-a||)+(F(x))||T(x-a)||+||x-a||, adica

(5)(GF)(x)=(GF)(a)+(ST)(x-a)+||x-a||S((x))+(F(x))||T(x-a)+(x)||x-a||||, xD

Fie acum (x)=S((x))+||T(x-a)+(x)||x-a|||| pentru xD si fie (a)=0

Sa aratam ca (x)=0.

Observam mai intai ca intrucat S=operator liniar S=continuu si atunci S((x))=0

De asemenea, este marginit intrucat iar T fiind operator liniar este continuu si, in consecinta , cf. th.67.8, marginita

Pe de alta parte, F fiind diferentiabila in a este si continua in a, adica F(x)=F(a)=b

Cum si atunci

In consecinta, din (5) obtinem:

(GF)(x)=(GF)(a)+(ST)(x-a)+||x-a||(x), xD cu , relatia ce exprima ca GF diferentiabila in a si ca d(GF)(a)=ST=dG(b)dF(a)=dG(F(a))dF(a).(am folosit faptul ca prin compunerea operatorilor liniari S si T s-a obtinut operatorul ST:RⁿR^p care este de asemenea liniar)

Corolar1

In ipoteza teoremei de mai sus are loc egalitatea:

(6) J_GF(a) =J_G(F(a).J_F(a)

Dem.

Am vazut ca functia dF(a) poate fi identificata cu matricea jacobiana J_F(a), dG(b)=dG(F(a)) cu matricea jacobiana J_G(F(a)), iar d(GF)(a) cu JGF(a)

Relatia (6) se obtine din teorema de mai sus, daca se tine seama ca avem 2 operatori liniari T:RⁿR^m si S:R^mR^p, atunci pentru matricile associate lor si operatorului liniar ST:RⁿR^p are loc egalitatea

(7)A_ST =A_S·A_T(fol th 6.7.8)

Observatie!

Din formula (6) vom obtine, prinparticularizari convenabile, diverse reguli de derivare compuse, reguli des utilizate in aplicatii.

Corolar2

Daca in ipoteza teoremei de mai sus, n=m=p, F=(f₁,f₂,..,f_n) ,G=(g₁,g₂,...,g_n) iar H=GF=(h₁,h₂,..,h_n), unde h_i(x₁,x₂,..,x_n)=g_i(f₁(x₁,x₂,..,x_n),..,f_n(x₁,x₂,..,x_n)), i= atunci

(8)

Dem.

Relatia (8)rezulta imediat din relatia (6) tinand seama de faptul ca determinantul produsului a 2 matrici patratice de ordin n coincide cu produsul determinantilor celor 2 matrici.

Observatie!

Se vede ca formula (8) genereaza formula (gf)'(a)=g'(f(a))·f'(a), care exprima derivate functiei compuse a 2 functii reale de o variabila reala, aceasta se obtine din relatia (8) pentru cazul n=m=p=1.

Corolar3

Fie D un deschis din R, un deschis din R² , f:D si g:R.Daca f-diferentiabila pe D iar g-diferentiabila pe , atunci pentru h=gf:DR are loc:

(9)       h'(t)=·u'(t)+·v'(t), D, unde f(t)=(u(t),v(t)), D.

dem.

Din relatia (6 avem) :

J_h(t)=J_g(f(t))·J_f(t), D

Adica h'(t)= ·u'(t)+·v'(t) ,

Corolar4

Fie D si - 2 deschisi din R², F:D si G:R - 2 functii diferentioabile respective pe D si .Daca H=GF:DR, F(x,y)=(u,v), (x,y), atunci

(10)

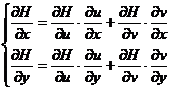
Dem.

Daca scriem (6) in punctual current (x,y) avem:

=· (10).

Teoreme de medie

In capitolul 1 am demonstrate celebra teorema a lui Lagramge, care ne asigura ca pentru orice functie f:[a,b]R continua pe [a,b] si derivabila pe (a,b) exista cel putin un punct c(a,b) a.i.

(*) f(b)-f(a)=f'(c)(b-a)

In cele ce urmeaza, plecand de la o analiza atenta a acestei teoreem, vom pune in evidenta doua forme ale acesteia pentru functii vectoriale:una pentru cazul functiilor definite pe submultimi ale lui Rⁿ cu valori reale si alta pentru functii definite pe submultimi ale lui Rⁿ cu valori in R^m.

Daca pentru prima teorema vom constata o forma analoga aceleia prezentate prin (*), vom fi oarecum surprinsi, la prima vedere, de cea de a doua forma care nu se mai exprima printr-o egalitate ci printr-o inegalitate.

Daca analizam insa atent (*) putem observa ca de fapt nu se stie nimic despre punctual c, decat ca se afla intre a si b si ca, in majoritatea cazurilor, f'(c) este un numar cuprins intre marginile inferioara si superioara ale functiei f' pe [a,b].Asa incat forma de inegalitate pe care o vom obtine in teorema15 este naturala intrucat exprima, in esenta, natura exacta a teoremei de medie.

Sa trecem acum la demonstrarea primei teoreme de medie pentru functii definite pe submultimi ale lui Rⁿ cu valori reale.

Teorema14 (teorema de medie pentru functii cu valori reale)

Fie [a,b] un segment din Rⁿ. Daca f:DR este diferentiabila pe un deschis D din Rⁿ care contine segmental [a,b], atunci exista un punct

= a.i.

(*) f(b)-f(a)=df()(b-a).

Dem.

Sa definim functia G:[0,1]D prin G(t)=a+t(b-a), t[0,1].Evident ca G este continua pe [0,1], G((0,1))=A si ca G este diferentiabila pe (0,1).Conform corolarului1 functia =fG:[0,1]R este diferentiabila pe (0,1) iar

(1) d(t)=df(G(t))dG(t), t

Daca h este arbitrar din R, atunci

(2) d(t)(h)=df(G(t)) dG(t)(h).

Dar

(3) d(t)(h)='(t)h

Iar (4) dG(t)(h)=(dg₁(t)(h),dg₂(t)(h),..,dg_n(t)(h))

(aici G=(g₁,g₂,...,g_n) cu g_i:[0,1]R, i=)

Inlocuind dg_i(t)(h)=g'_i(t)h in relatia (4) avem

(4') dG(t)(h)=(g'₁(t)h,g'₂(t)h,..,g'_n(t)h)

Care, introdusa in relatia (2), impreuna cu (3), antreneaza

'(t)h=df(G(t))( g'₁(t)h,g'₂(t)h,..,g'_n(t)h)

Sau

(5) '(t)=df (G(t))( g'₁(t),g'₂(t),..,g'_n(t)).

Daca a=(a₁,a₂,...,a_n) si b=(b₁,b₂,..,b_n), atunci g'_i(t)=b_i-a_i , i= si deci din (5) obtinem (6) '(t)=df(G(t))(b₁-a₁,b₂-a₂,..,b_n-a_n)=df(G(t))(b-a) .

Observam acum ca functia :[0,1]R satisface conditiile teoremei lui Lagrange intrucat este continua pe [0,1], fiind compunerea functiilor continue G si f, si este derivabila pe (0,1).Atunci exista un punct (0,1) a.i.

(7) (1)-(0)=

Dar (1)=f(b) si (0)=f(a) si atunci relatia (7) devine, tinand seama si de relatia (6),f(b)-f(a)=df(G())(b-a),

Unde

G()=a+(b-a)A.

Notand acum cu =G(), obtinem

f(b)-f(a)=df()(b-a), adica (*).

Observatie!

In principal, teorema va fi aplicata pentru a estima diferenta intre f(x+h) si f(x) atunci cand se cunoaste h.

Corolar5

Daca in ipotezele teoremei precedente multimea este majorata de M, atunci

(1)      |f(b)-f(a)|≤M||b-a||, unde ||df(u)|| inseamna norma operatorului df(u).

Dem.

Fie M>0 a.i. ||df(u)||≤M, uD.Tinand seama de urmatoarea teorema:Daca T:RⁿR^m este un operator liniar, atunci T este operator continuu. Precum si de inegalitatea (*) din cap.6.7 care asigura ca daca T:XY este un operator liniar continuu intre doua spatii normate, atunci

||T(x)||≤||T||·||x||, xX, obtinem din (*)

|f(b)-f(a)|=||df()(b-a)||≤||df()||·||b-a||≤M||b-a||.

Teorema15 (teorema de medie pentru functii vectoriale)

fie functia F:DR^m, unde D este un deschis din Rⁿ (n≥1,m≥1), diferentiabila pe D.Daca exista M>0a.i.

(1) ||dF(x)||≤M,pentru xC, unde C este o multime convexa inclusa in D, atunci pentru orice doua puncte a,bC are loc inegalitatea:

(2) ||F(b)-F(a)||≤M||b-a||.

Dem.

Fie functia auxiliara :[0,1]R^m definite prin

(3)(t)=F(a+t(b-a)), t[0,1]R.

Se vede ca(1)=F(b) si (0)=F(a).

Fie >0 arbitrar.Sa notam prin

A=.

Intrucat este obtinuta prin compunerea a doua functii diferentiabile este o functie diferentiabila, deci continua, atunci A este multime inchisa.

In acelasi timp, se observa ca A este nevida (contine cel putin punctul 0) si marginita.Prin urmare, A este multime compacta.

Fie =supA.Cum A este compacta si este punct adherent multimii A rezulta ca A.Tinand seama de continuitatea lui in 0 rezulta ca exista >0 a.i.

|| (t)- (0)||< ≤Mt||b-a||+t+, pentru |t|<, ceea ce antreneaza ca exista cel putin un punct t>0 a.i. t, prin urmare >0.

Sa aratam ca =1.In adevar, daca am presupune ca <1, intrucat a+(b-a)(a,b)=[a,b] iar f este diferentiabila pe D, rezulta diferentiabila in si atunci pentru 0<t<are loc inegalitatea

|| +t ) - )||≤||d )||t+t≤Mt||b-a||+t

De aici obtinem

|| +t ) -(0)||≤|| +t ) - (0)||≤

≤Mt||b-a||+t+M||b-a||+

=M(+t)||b-a||+(+t)

Care spune ca +t , ceea ce contrazice faptul ca =supA.Deci =1.

Atunci, tinand seama ca =1, avem:

||||≤M||b-a||+2;

Cum este arbitrar,

||F(b)-F(a)||≤M||b-a||.

De aici rezulta imediat:

Corolar6

fie F:DR^m , unde D este un deschis Rⁿ (n≥1,m≥1), diferentiabila pe D.Daca a,b a.i. segmental [a,b]D, atunci are loc inegalitatea:

||F(b)-F(a)||≤||b-a|||dF(x)||