
|
|
|
SISTEMUL DE INDICATORI CE CARACTERIZEAZA
SERIILE CRONOLOGICE
I. INDICATORII ABSOLUTI
![]() u.m.
u.m. ![]() .
.
![]()
![]() modificarea absoluta cu baza in lant.
modificarea absoluta cu baza in lant.
![]() u.m.
u.m. ![]() .
.
Relatii utile :
![]() u.m.,
u.m., ![]()
![]() u.m.,
u.m., ![]()
II. INDICATORII RELATIVI
![]()
![]() sau
sau ![]()
![]() - indicele de dinamica calculat cu baza fixa, exprimat sub forma de
coeficient sau procentual.
- indicele de dinamica calculat cu baza fixa, exprimat sub forma de
coeficient sau procentual.
![]()
![]() sau
sau ![]()
![]() indicele de dinamica calculat cu baza in
lant.
indicele de dinamica calculat cu baza in
lant.
Relatii utile :![]() unde
unde![]()
![]() , unde
, unde ![]() .
.
![]() ritmul de dinamica cu baza fixa :
ritmul de dinamica cu baza fixa :
![]() sau
sau ![]()
![]() ritmul de dinamica cu baza in lant :
ritmul de dinamica cu baza in lant :
![]() sau
sau ![]() ,
, ![]() .
.
![]() valoarea absoluta a unui procent de dinamica
cu baza fixa :
valoarea absoluta a unui procent de dinamica
cu baza fixa :
![]() sau
sau ![]()
![]() valoarea absoluta a
unui procent de dinamica cu baza in lant :
valoarea absoluta a
unui procent de dinamica cu baza in lant :
![]() ,
, ![]() .
.
III. INDICATORII MEDII
nivelul mediu pentru o serie cronologica de intervale de timp :
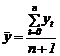 u.m.
u.m.
nivelul mediu pentru o serie de momente cu intervale egale intre momente :
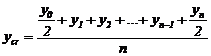 u.m.
u.m.![]()
nivelul mediu pentru o serie de momente cu intervale neegale intre momente :
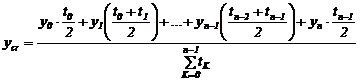 u.m.
u.m. ![]()
Observatie. ![]() se numeste medie
cronologica simpla;
se numeste medie
cronologica simpla;
![]() se numeste medie
cronologica ponderata, fiind singurul indicator mediu care caracterizeaza o
serie de momente cu intervale neegale intre datele inregistrate.
se numeste medie
cronologica ponderata, fiind singurul indicator mediu care caracterizeaza o
serie de momente cu intervale neegale intre datele inregistrate.
modificarea medie absoluta :
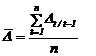 u.m. sau
u.m. sau![]() u.m. .
u.m. .
indicele mediu de dinamica :
![]() sau
sau ![]()
ritmul mediu de dinamica :
![]() .
.
AJUSTAREA SERIILOR CRONOLOGICE
Seria cronologica poate fi definita ca o succesiune de valori numerice ordonate in timp, valori care se modifica datorita influentelor de natura sistematica si a altora de tip aleator.
Componentele sistematice ale unei serii cronologice sunt:
tendinta centrala sau trendul;
oscilatii (variatii) periodice datorate diferitelor cauze dintre care cele mai frecvente sunt oscilatiile sezoniere care se repeta ritmic cu o periodicitate constanta mai mica de un an (semestru, trimestru, luna, decada);
ciclicitatea care se prezinta sub forma de fluctuatii in jurul tendintei, inregistrate la perioade mai mari de un an.
Componentele aleatoare se manifesta ca devieri de la linia evolutiei sistematice, ca efect al actiunii unor factori accidentali, spontani, imprevizibili, etc.
Valoarea ajustata este acea valoare obtinuta prin calcul pe baza unei functii matematice de ajustare.
Dispersia totala se noteaza si se defineste astfel :

Dispersia termenilor seriei de la valorile ajustate sintetizeaza influenta factorilor reziduali (factori neinregistrati care la seriile cronologice sunt toti cei care produc modificari cu exceptia factorului timp) si se calculeaza dupa formula:
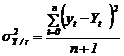
unde ![]() este valoarea
teoretica a variabilei y obtinuta prin ajustare in raport cu timpul.
Dispersia valorilor ajustate de la valoarea medie se noteaza cu
este valoarea
teoretica a variabilei y obtinuta prin ajustare in raport cu timpul.
Dispersia valorilor ajustate de la valoarea medie se noteaza cu ![]() care sintetizeaza numai variatia produsa de
modificarea factorului timp.
care sintetizeaza numai variatia produsa de
modificarea factorului timp.
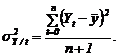
Metodele de ajustare pot fi simple (metoda mediilor mobile, metoda grafica, metoda modificarii mediei absolute, metoda indicelui mediu de dinamica) sau analitice, care au la baza un model matematic.
Metoda mediilor mobile este specifica seriilor care prezinta oscilatii sezoniere sau ciclice.
Mediile mobile sunt medii aritmetice simple calculate dintr-un numar prestabilit de termeni (par sau impar) in functie de periodicitatea influentei factorilor sezonieri.
Ajustarea cu medii mobile dintr-un numar par de termeni se face in doua trepte:
medii mobile
provizorii ![]()
medii mobile definitive (sau centrate)![]() , care se plaseaza in dreptul
termenilor seriei si reprezinta valorile ajustate ale termenilor respectivi din
seria initiala.
, care se plaseaza in dreptul
termenilor seriei si reprezinta valorile ajustate ale termenilor respectivi din
seria initiala.
Metoda grafica este un procedeu care consta in reprezentarea grafica a seriei de date empirice prin cronograma (historiograma) si apoi se traseaza vizual, dreapta sau curba care uneste cele doua puncte extreme ale seriei dinamice, astfel incat sa aiba abateri minime fata de pozitia valorilor reale in grafic.
Metoda modificarii mediei absolute.
Procedeul se utilizeaza atunci cand sirul de date privind nivelurile fenomenului se aseamana cu o progresie aritmetica, deci modificarile absolute cu baza in lant au valori aproape constante.
Functia de ajustare :
![]() u.m., unde
u.m., unde ![]()
sau
![]() unde :
unde :
![]() reprezinta termenul
luat ca baza de ajustare (acea valoare care se apropie cel mai mult de dreapta
sau curba trasata vizual pe
reprezinta termenul
luat ca baza de ajustare (acea valoare care se apropie cel mai mult de dreapta
sau curba trasata vizual pe
grafic);![]()
![]() reprezinta variabila
timp in raport cu baza de ajustare folosita (pozitia pe care o are termenul
respectiv fata de cel ales ca baza de ajustare);
reprezinta variabila
timp in raport cu baza de ajustare folosita (pozitia pe care o are termenul
respectiv fata de cel ales ca baza de ajustare);![]()
Metoda indicelui mediu de dinamica.
Ajustarea prin
acest procedeu se utilizeaza in cazul in care sirul termenilor ![]() urmeaza aproximativ o
progresie geometrica.
urmeaza aproximativ o
progresie geometrica.
Functia de ajustare :
![]() u.m., unde
u.m., unde ![]()
sau
![]() u.m.,
u.m.,
unde ![]() ,
, ![]() sunt cei
din
sunt cei
din ![]() si
respectiv
si
respectiv ![]() .
.
Metodele analitice de ajustare
Metodele analitice sunt folosite pentru
estimarea cat mai corecta a tendintei generale descrise de fenomene in timp si
in acest scop s-a apelat la conceptul de functie de ajustare : ![]() , unde
, unde
t - reprezinta valorile variabilei independente (timpul);
y - reprezinta valorile variabilei dependente (fenomenele) care sunt prezentate in seria cronologica.
Criteriile folosite pentru alegerea tipului de functie care se potriveste cel mai bine pentru exprimarea trendului, aplicabile optional :
criteriul bazat pe reprezentarea grafica : se construieste cronograma si forma ei sugereaza un model matematic de functie;
criteriul diferentelor : se calculeaza diferentele
absolute cu baza in lant de ordinul unu din termenii seriei ![]() , de ordinul doi
, de ordinul doi ![]() etc. pana obtinem diferentele de ordin k aproximativ constante si se apreciaza ca seria cronologica are o
tendinta ce poate fi modelata printr-un polinom de gradul k ;
etc. pana obtinem diferentele de ordin k aproximativ constante si se apreciaza ca seria cronologica are o
tendinta ce poate fi modelata printr-un polinom de gradul k ;
daca indicii cu baza in lant sunt constanti, admitem ca seria cronologica prezinta o tendinta exponentiala.
Dupa stabilirea modelului de
ajustare se trece la estimarea parametrilor calculati pe principiul ca suma
patratelor diferentelor dintre valorile empirice (![]() ) si cele teoretice (
) si cele teoretice (![]() ) sa fie minime (metoda celor
mai mici patrate) :
) sa fie minime (metoda celor
mai mici patrate) :
![]()
Modelul liniar. ![]() ,
, ![]() , unde:
, unde:
![]() ,
, ![]() sunt valorile
caracteristicii factoriale, care in cazul seriilor cronologice este timpul ;
sunt valorile
caracteristicii factoriale, care in cazul seriilor cronologice este timpul ;
a este parametrul care are valoarea egala cu media seriei si arata ce nivel ar fi atins y daca influenta tuturor factorilor cu exceptia celui inregistrat ar fi constanta pe toata perioada;
b sintetizeaza numai influenta caracteristicii factoriale;
![]() sunt valorile ajustate calculate in functie de valorile
caracteristicii factoriale
sunt valorile ajustate calculate in functie de valorile
caracteristicii factoriale ![]() .
.
Consideram ![]() si conform metodei
celor mai mici patrate punctul stationar
si conform metodei
celor mai mici patrate punctul stationar ![]() al functiei
al functiei ![]() realizeaza minimul
functiei. Solutia
realizeaza minimul
functiei. Solutia ![]() este a sistemului:
este a sistemului:
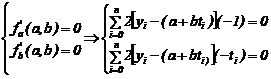
 sistem liniar , care
admite solutia:
sistem liniar , care
admite solutia:
![]()
![]() , unde
, unde 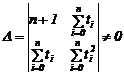 ,
, 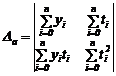 ,
, 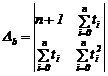 , stabilind in prealabil numarul de cifre care vor fi luate
in considerare dupa virgula, atunci cand este cazul. Valorile ajustate ale caracteristicii rezultative sunt :
, stabilind in prealabil numarul de cifre care vor fi luate
in considerare dupa virgula, atunci cand este cazul. Valorile ajustate ale caracteristicii rezultative sunt : ![]()
![]()
Analizand gradul de dependenta dintre
caracteristica de timp ![]() si caracteristica
rezultativa
si caracteristica
rezultativa ![]() , se poate constata ca
, se poate constata ca ![]() nu este in functie de
timp. }n general, orice fenomen social-economic depinde de mai multi factori a
caror influenta este prezenta in toate unitatile de timp. Astfel, productia
depinde printre altele de gradul de
inzestrare tehnica, de gradul de calificare a muncii, de modul de organizare a
procesului de munca etc. Pentru a anula influenta variatiei de timp, se pune
conditia
nu este in functie de
timp. }n general, orice fenomen social-economic depinde de mai multi factori a
caror influenta este prezenta in toate unitatile de timp. Astfel, productia
depinde printre altele de gradul de
inzestrare tehnica, de gradul de calificare a muncii, de modul de organizare a
procesului de munca etc. Pentru a anula influenta variatiei de timp, se pune
conditia ![]()
Modelul parabolic ![]() ,
, ![]() .
.
Folosind ![]() obtinem sistemul :
obtinem sistemul :
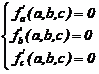
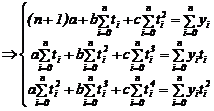
numit ca si in cazul modelului
liniar, sistem de ecuatii normale. Solutia lui ![]() ne permite calculul valorilor ajustate
ne permite calculul valorilor ajustate ![]() .
.
Modelul
hiperbolic ![]() are sistemul de
ecuatii normale:
are sistemul de
ecuatii normale:

Modelul exponential ![]() prin logaritmare se transforma intr-un model
liniar
prin logaritmare se transforma intr-un model
liniar ![]() , iar sistemul de ecuatii
normale este :
, iar sistemul de ecuatii
normale este :
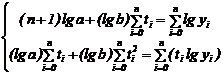
Cu (![]() ) solutia sistemului anterior determinam:
) solutia sistemului anterior determinam: ![]()
![]() si prin
antilogaritmare aflam
si prin
antilogaritmare aflam ![]() .
.
Criterii de alegere a procedeelor de ajustare
Calculam ![]() si consideram ca
modelul care corespunde este acela pentru care suma calculata are valoarea cea
mai mica.
si consideram ca
modelul care corespunde este acela pentru care suma calculata are valoarea cea
mai mica.
Determinam in prealabil abaterea medie liniara a valorilor reale de la valorile ajustate
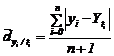 si calculam coeficientul de variatie
si calculam coeficientul de variatie ![]() alegerea modelului se face pe acelasi
principiu ca mai sus.
alegerea modelului se face pe acelasi
principiu ca mai sus.
Extrapolarea seriilor cronologice
Metodele si procedeele folosite pentru
ajustarea termenilor unei (SCR) sunt folosite si pentru extrapolare. Termenii
ce urmeaza a fi calculati sunt valori teoretice si ii vom nota cu ![]() ca sa-i distingem de
ca sa-i distingem de ![]() , iar variabila timp va fi
, iar variabila timp va fi ![]()
Prognozele sunt fundamentate atunci cand numarul de termeni este suficient de mare (cel putin 6-7 termeni) si la culegerea datelor tinem seama de evolutia fenomenului in timp.
Formulele de calcul sunt :
![]() -pe baza sporului mediu,
-pe baza sporului mediu,
![]() -pe baza indicelui mediu de crestere,
-pe baza indicelui mediu de crestere,
![]() -pentru modelul liniar,
-pentru modelul liniar,
![]() -pentru modelul parabolic.
-pentru modelul parabolic.
PROBLEME REZOLVATE
1. Analiza statistica a unei serii cronologice de intervale.
Evolutia productiei fizice (mii de bucati) la societatea "MEDIMPACT" S.A. pentru perioada 1990-1999 la produsul de baza (incaltaminte), se prezinta in tabelul nr.1.
Anul
1990
1991
1992
1993
1994
1995
1996
1997
1998
1999
Productia fizica
(mii.buc)
1940
1118
870
768
796
640
645
700
672
686
Se cere: a) sa se caracterizeze evolutia productiei fizice (mii buc.) folosind indicatorii:
-absoluti;
-relativi;
-medii.
b) sa se reprezinte grafic seria valorilor
c) folosind metodele mecanice si analitice, determinati trendul de evolutie;
d) alegeti metoda cea mai adecvata care ajusteaza fenomenul si sa se extrapoleze seria pentru anii 2000, 2001, 2002.
Rezolvare:
a) Calculul indicatorilor absoluti:
-nivelul absolut ![]() este reprezentat de
termenii seriei din tabelul nr.1 randul 2. Facem mentiunea ca
este reprezentat de
termenii seriei din tabelul nr.1 randul 2. Facem mentiunea ca ![]() mii bucati, deci
mii bucati, deci
![]() .
.
nivelul
totalizat : ![]() mii bucati
mii bucati
modificari absolute (![]()
cu baza fixa ![]() mii bucati (tabelul 2, col.2)
mii bucati (tabelul 2, col.2)
![]() mii bucati
mii bucati
![]() mii bucati
mii bucati
.
![]() mii bucati
mii bucati
cu baza
in lant ![]() mii bucati (tabelul 2,
col.3)
mii bucati (tabelul 2,
col.3)
![]() mii bucati.
mii bucati.
![]() mii bucati.
mii bucati.
..
![]() mii bucati
mii bucati
-Relatii intre ![]() si
si ![]() :
:
![]()
![]() mii bucati
mii bucati
![]() mii bucati
mii bucati
![]() mii bucati
mii bucati ![]()
![]() mii bucati.
mii bucati.
![]() mii bucati
mii bucati
Calculul indicatorilor absoluti
Tabelul nr.2
Anul
Productia fizica
(mii buc)
![]()
Modificarea absoluta (mii buc.)
Cu baza fixa
![]()
Cu baza in lant
![]()
0
1
2
3
1990
![]() 1940
1940
0
1991
![]() 1118
1118![]()
-822
-822
1992
![]() 870
870
-1070
-248
1993
![]() 768
768
-1172
-102
1994
![]() 796
796
-2736
+28
1995
![]() 640
640
-1300
-156
1996
![]() 645
645
-1295
+5
1997
![]() 700
700
-1240
+ 55
1998
![]() 672
672
-1268
- 28
1999
![]() 686
686
-1254
+ 14
Total
![]()
![]()
Calculul indicatorilor relativi :
Indicele de dinamica (crestere/descrestere) :
cu baza
fixa ![]() - tabelul nr.3 col.2
- tabelul nr.3 col.2
![]()
![]() 57,628% 57,63%
57,628% 57,63%
..
![]() 35,360%s35,36%
35,360%s35,36%
cu baza in lant ![]() tabelul nr.3 col.3
tabelul nr.3 col.3
![]() 57,628% 57,63%
57,628% 57,63%
![]() 77,817% 77,82%
77,817% 77,82%
![]() 102,083% 102,08%
102,083% 102,08%
Relatiile de legatura :![]()
![]()
![]()
Calculul indicatorilor relativi
Tabelul nr.3
Anul
yt
(mii buc)
Indicele de dinamica
Ritmul
Valoarea absoluta a 1% din ritm
It/o%
It/t-1%
Rt/o
Rt/t-1
At/o
At/t-1
0
1
2
3
4
5
6
7
1990
![]() 1940
1940
100
0
1991
1118
57,63
57,63
- 42,37
- 42,37
19,4
19,40
1992
870
44,85
77,82
- 55,15
- 22,18
19,4
11,18
1993
768
39,59
88,28
- 60,41
- 11,72
19,4
8,70
1994
796
41,05
103,65
- 58,95
3,65
19,4
7,68
1995
640
32,99
80,40
- 67,01
- 19,60
19,4
7,96
1996
645
33,25
100,78
- 66,75
0,78
19,4
6,40
1997
700
36,08
108,53
- 63,92
8,53
19,4
6,45
1998
672
34,64
96,00
- 65,36
- 4,00
19,4
7,00
1999
686
35,36
102,08
- 64,64
2,08
19,4
6,72
Total
8835
Ritmul de modificare (crestere/descrestere) :
cu baza
fixa ![]() (vezi tabelul nr.3 col
4)
(vezi tabelul nr.3 col
4)
![]() 100-100 s 0
100-100 s 0
![]() 57,63 - 100 s -42,37
57,63 - 100 s -42,37
![]() 35,36 - 100 s -64,64
35,36 - 100 s -64,64
cu baza
in lant ![]() (vezi tabelul nr.3
col.5)
(vezi tabelul nr.3
col.5)
![]()
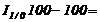 57,63 - 100 s -42,37
57,63 - 100 s -42,37
![]() 77,82 - 100 s - 22,18
77,82 - 100 s - 22,18
![]() 102,8 - 100 s 2,08
102,8 - 100 s 2,08
Valoarea absoluta a unui procent din ritmul modificarii (A) :
cu baza
fixa ![]() mii bucati (vezi tabelul nr.3 col.6)
mii bucati (vezi tabelul nr.3 col.6)
![]() 19,4 mii bucati
19,4 mii bucati
![]() 19,4 mii bucati
19,4 mii bucati
cu baza
in lant ![]() mii bucati (vezi
tabelul nr.3 col.7)
mii bucati (vezi
tabelul nr.3 col.7)
![]() 19,4 mii bucati
19,4 mii bucati
![]() 11,18 mii bucati
11,18 mii bucati
.
![]() 6,72 mii bucati
6,72 mii bucati
Calculul indicatorilor medii.
Nivelul
mediu absolut (![]() ) : seria cronologica din acest exemplu este o serie pe
intervale pentru care nivelul mediu se calculeaza aplicand formula mediei
aritmetice:
) : seria cronologica din acest exemplu este o serie pe
intervale pentru care nivelul mediu se calculeaza aplicand formula mediei
aritmetice:
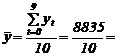 88,35 mii bucati.
88,35 mii bucati.
Productia fizica medie anuala a fost de 88,35 mii bucati.
Modificarea medie absoluta (![]() ) :
) :
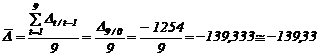 mii bucati.
mii bucati.
In medie s-a inregistrat in perioada 1990-1999 o descrestere anuala de 139,33 mii bucati.
Indicele mediu (![]() ) :
) :
![]() sau
sau
Ritmul mediu (![]() ) :
) :
![]()
c) Metode mecanice pentru determinarea tendintei generale (a trendului)
![]() Metoda modificarii
medii absolute
Metoda modificarii
medii absolute
![]() mii bucati
mii bucati
![]()
![]() Metoda indicelui mediu
Metoda indicelui mediu
![]() mii bucati
mii bucati
![]()
Valorile ajustate prin aceste doua metode sunt prezentate in tabelul nr. 4 coloanele 3 respectiv 4.
Tabelul nr. 4
Anul
![]()
![]()
Valori ajustate
prin :
modificarea medie absoluta
![]() mii buc.
mii buc.
indicele mediu
![]() mii buc.
mii buc.
0
1
2
3
4
1990
1940
0
![]()
1991
1118
1
![]()
1992
870
2
![]()
1993
768
3
![]()
1994
796
4
![]()
1995
640
5
![]()
1996
645
6
![]()
1997
700
7
![]()
1998
672
8
![]()
1999
686
9
![]()
Total
8835
![]()
![]() Metode analitice
Metode analitice
Cronograma din fig. nr. 1 indica o evolutie parabolica sau hiperbolica.
Pentru ajustarea parabolica ![]()
![]() , iar sistemul de ecuatii
normale este:
, iar sistemul de ecuatii
normale este:
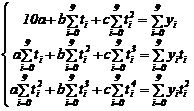
}n tabelul nr. 5
sunt efectuate calculele necesare rezolvarii sistemului, dar si valorile ajustate
![]() ,
, ![]() . Seria are 10 ani, deci mijlocul seriei este intre 1994 si 1995, deci
. Seria are 10 ani, deci mijlocul seriei este intre 1994 si 1995, deci ![]() ,
, ![]() .
.
Tabelul nr. 5
Anii
![]()
![]()
![]()
![]()
![]()
![]()
![]()
0
1
2
3
4
5
6
7
1990
1940
-9
81
-729
6561
-17460
157140
1991
1118
-7
49
-343
2401
-7826
54782
1992
870
-5
25
-125
625
-4350
21750
1993
768
-3
9
-27
81
-2304
6912
1994
796
-1
1
-1
1
-796
796
1995
640
1
1
1
1
640
640
1996
645
3
9
27
81
1935
5805
1997
700
5
25
125
625
3500
17500
1998
672
7
49
343
2401
4704
32928
1999
686
9
81
729
6561
6174
55566
Total
8835
0
330
0
19338
-15783
353819
Sistemul de ecuatii normale este
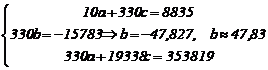
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]()
![]() .
.
Deci ![]() ,
, ![]()
Tabelul nr. 5
![]()
![]()
![]()
![]()
8
9
10
11
430,47
670,67
1101,14
1741,42
334,81
361,13
695,94
1336,22
239,15
184,25
423,40
1063,68
143,49
66,33
209,82
850,10
47,83
7,37
55,20
695,48
-47,83
7,37
-40,46
599,82
-143,49
66,33
-77,16
563,12
-239,15
184,25
-54,90
585,38
-334,81
361,13
26,32
666,60
-430,47
670,67
240,20
880,48
8982,30
Pentru trendul hiperbolic calculele necesare
determinarii solutiei ![]() a sistemului de ecuatii normale si valorile
ajustate sunt prezentate in tabelul nr. 6.
a sistemului de ecuatii normale si valorile
ajustate sunt prezentate in tabelul nr. 6.
Tabelul nr. 6
Anul
![]()
![]()
![]()
![]()
![]()
![]()
![]()
0
1
2
3
4
5
6
7
1990
1940
-9
![]()
![]()
-215,56
20,38
903,88
1991
1118
-7
![]()
![]()
-159,71
26,21
909,71
1992
870
-5
![]()
![]()
-174,00
36,69
920,19
1993
768
-3
![]()
![]()
-256,00
61,15
944,65
1994
796
-1
![]()
![]()
-796,00
183,45
1066,95
1995
640
1
![]()
![]()
640,00
-183,45
700,05
1996
645
3
![]()
![]()
215,00
-61,15
822,35
1997
700
5
![]()
![]()
140,00
-36,69
846,81
1998
672
7
![]()
![]()
96,00
-26,21
857,29
1999
686
9
![]()
![]()
76,22
-20,38
863,12
Total
8835
0
2,366
-434,05
8835,00
Sistemul ![]() are solutia
are solutia  .
.
d) Comparand ![]() cu
cu ![]() observam ca
observam ca ![]()
![]() pentru valorile
ajustate dupa modelul hiperbolic, deci acesta ar fi cel care corespunde.
pentru valorile
ajustate dupa modelul hiperbolic, deci acesta ar fi cel care corespunde.
}n tabelul nr. 7 vom calcula ![]() luand
luand ![]() state cu fiecare dintre modelele utilizate.
state cu fiecare dintre modelele utilizate.
Tabelul nr. 7
Valori ajustate prin:
Anii
![]()
Modificarea
medie
absoluta
Indicele mediu
Functia parabolica
Functia hiperbolica
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
0
1
2
3
4
5
6
7
8
9
1990
1940
0
0
198,58
39434,0164
1036,12
1073544,6544
1991
1118
682,67
466038,3289
218,22
47619,9684
208,29
43384,7241
1992
870
791,34
626218,9956
193,68
37511,9424
50,19
2519,0361
1993
768
754,01
568531,0801
82,10
6740,41
176,65
31205,2225
1994
792
586,68
344193,4224
100,52
10104,2704
270,95
73413,9025
1995
640
603,35
364031,2225
40,18
1614,4324
60,5
3660,25
1996
645
459,20
210864,64
81,88
6704,3344
177,35
31453,0225
1997
700
264,69
70060,7961
114,62
13137,7444
146,81
21553,1761
1998
672
153,36
23519,2896
5,4
29,16
185,29
34332,3841
1999
686
0,03
0,009
194,48
37822,4704
177,12
31371,4944
Total
8835
4295,33
2673457,7842
1229,66
200718,7495
2489,27
1346437,8667
Calculul coeficientilor de variatie
Tabelul nr. 8
Nr.
crt.
Metoda
de
ajustare
prin
![]()
![]()
![]()
![]()
0
1
2
3
4
5
1.
Modificarea medie
absoluta
2673 457,7842
517,0549
5,852
4,8617
2.
Indicele mediu
3.
Functia parabolica
200718,7495
141,675
1,604
1,3918
4.
Functia
hiperbolica
1346437,8667
366,938
4,153
2,8175
-compararea abaterilor
absolute ale valorilor teoretice (ajustate) fata de cele empirice ![]() conduce la alegerea modelului parabolic.
conduce la alegerea modelului parabolic.
-compararea patratelor
abaterilor dintre valorile empirice si cele ajustate ![]() conduce la aceeasi alegere ca mai sus.
conduce la aceeasi alegere ca mai sus.
-compararea coeficientilor de variatie calculati dupa relatiile :
 (vezi tabelul nr. 8
coloana 4)
(vezi tabelul nr. 8
coloana 4)
sau
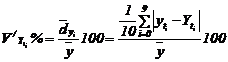 (vezi tabelul nr. 8
coloana 5)
(vezi tabelul nr. 8
coloana 5)
conduce la alegerea modelului parabolic.
Extrapolam productia fizica pentru urmatorii doi ani, considerand ca sunt aceleasi conditii si prezentam rezultatele in tabelul nr. 9.
Tabelul nr. 9
Nr.
crt.
Metode de ajustare
2000
2001
0
1
2
3
1.
Modificarea medie
absoluta
![]()
![]()
2.
Indicele
mediu
![]()
![]()
3.
Functia
parabolica
![]()
![]()
4.
Functia hiperbolica
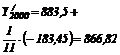
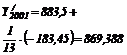
2. Se cunosc urmatoarele date privind importurile de calculatoare in perioada 1992-2000.
Tabelul nr. 10
Anul
1993
1994
1995
1996
1997
1998
1999
2000
2001
Modificari
fata de
anul
precedent
(mld. lei)
46
28
40
42
43
47
51
49
55
Se cere:
a) reconstituirea seriei de valori absolute, stiind ca valoarea importului a crescut in perioada 1992-2000, in medie cu 21,25%;
b) sa se calculeze indicatorii medii si sa se interpreteze rezultatele;
c) sa se ajusteze seria printr-un procedeu analitic adecvat;
d) sa se calculeze coeficientul de variatie.
Rezolvare. a) }n randul 2 din tabelul nr. 10
sunt prezentate ![]() avand ca baza de
comparatie anul 1992.
avand ca baza de
comparatie anul 1992.
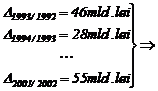
![]()
![]() .
.
Valoarea importului a crescut in perioada 1992-2000,
in medie cu 21,25%, adica ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Dar ![]()
![]()
![]() .
.
Asadar, 
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Folosim modificarile absolute cu baza in lant ca sa determinam termenii initiali ai seriei:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Seria cautata este prezentata in tabelul nr. 11.
Tabelul nr. 11
Anul
1992
1993
1994
1995
1996
1997
1998
1999
2000
2001
Import
de calculatoare
(mld. lei)
86
132
160
200
242
285
332
383
432
487
b) Indicatorii medii :
![]() nivelul mediu
nivelul mediu  , adica s-au importat in medie, anual, calculatoare in
valoare de
, adica s-au importat in medie, anual, calculatoare in
valoare de ![]()
![]() modificarea medie absoluta
modificarea medie absoluta 
![]()
![]() ritmul mediu a fost dat
ritmul mediu a fost dat ![]() si pe baza lui s-a
determinat indicele mediu de crestere
si pe baza lui s-a
determinat indicele mediu de crestere ![]()
c) }ntocmim cronograma si in functie de forma sa alegem modelul analitic.
Graficul sugereaza o evolutie liniara, deci alegem
![]() ,
, ![]() .
.
Sistemul ecuatiilor normale: 
![]() .
.
Pentru determinarea parametrilor modelului liniar intocmim tabelul nr. 12.
Tabelul nr. 12
Ani
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
0
1
2
3
4
5
6
7
8
9
1992
86
-9
81
-774
-198
75,9
10,1
10,1
102,01
1993
132
-7
49
-924
-154
119,8
12,2
12,2
148,84
1994
160
-5
25
-800
-110
163,9
-3,9
3,9
15,21
1995
200
-3
9
-600
-66
207,9
-7,9
7,9
62,41
1996
242
-1
1
-242
-22
251,9
-9,9
9,9
98,01
1997
285
1
1
285
22
295,9
-10,9
10,9
118,81
1998
332
3
9
996
66
339,9
-7,9
7,9
62,41
1999
383
5
25
1915
110
383,9
-0,9
0,9
0,81
2000
432
7
49
3024
154
427,9
4,1
4,1
16,81
2001
487
9
81
4383
198
471,9
15,1
15,1
228,01
Total
2739
0
330
7263
2738,9
82,9
8533,3
Sistemul ![]() devine
devine ![]()
![]()
![]()
![]()
![]() .
.
d) Calculam ambii coeficienti de variatie:
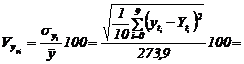
![]()
![]()
![]()
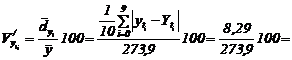
![]()
![]()
Valoarea lor este mica, deci apreciem ca ![]() aproximeaza teoretic destul de bine valorile
empirice.
aproximeaza teoretic destul de bine valorile
empirice.
SERII CRON.CONT.
3. Se cunosc urmatoarele date cu privire la numarul de hoteluri si moteluri in Romania in perioada 1988-1995:
Tabelul nr.13
Anul
1988
1989
1990
1991
Modificari absolute fata de anul precedent
10
8
2
-8
Modificari relative fata de anul precedent (%)
1,2346
0,9756
0,2415
-0,9639
Continuare
1992
1993
1994
1995
Modificari absolute fata de anul precedent
34
34
34
5
Modificari relative fata de anul precedent (%)
4,1363
3,9720
0,0382
0,5411
Se cere: a) sa se reconstituie seria de valori
b) sa se calculeze toti indicatorii absoluti si relativi.
Rezolvare:
a)
Cunoastem modificarile absolute fata de anul
precedent, adica ![]() t
s 1988, 1989,,1995 si modificarile relative fata de anul precedent (%) adica
t
s 1988, 1989,,1995 si modificarile relative fata de anul precedent (%) adica
![]() ,t
s 1988, 1989, , 1995, deci putem defini valoarea absoluta a unui procent de
dinamica cu baza in lant (
,t
s 1988, 1989, , 1995, deci putem defini valoarea absoluta a unui procent de
dinamica cu baza in lant (![]() ):
):
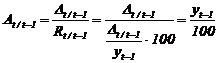 t s 1988, 1989,,1995.
t s 1988, 1989,,1995.
Calculele sunt prezentate in tabelul nr.14.
Determinarea valorilor absolute.
Tabelul nr.14.
Anul
![]()
![]()
![]()
![]()
0
1
2
3s1 2
4
1987
810
1988
10
1,2346
8,099 8,10
820
1989
8
0,9756
8,200 8,20
828
1990
2
0,2415
8,281 8,28
830
1991
-8
-0,9639
8,299 8,30
822
1992
34
4,1363
8,219 8,22
856
1993
34
3,9720
8,559 8,56
890
1994
34
0,0382
8,900 8,90
924
1995
5
0,5411
9,240 9,24
929
Total
Pentru y1995 folosim D1995/1994 s y1995- y1994 T y1995 s y1994 + D1995/1994 s 924 + 5 s 929 si completam in tabelul nr.14 coloana 4 ultima rubrica.
Cunoscand R1995/1994 putem determina I1995/1994% s R1995/1994 + 100%, adica
I1995/1994% s 0,5411 + 100 s 100,5411% T
I1995/1994 s 1,005411
9I1995/1994 s y1995/y1994 T y1995 s y1994 1,005411 s 924 1,005411 s 928,9 929
b) Indicatorii absoluti si relativi pentru seria reconstituita sunt prezentati in tabelul nr.15.
Tabelul nr.15
yt
Dt/t-1
Dt/0
Rt/t-1
Rt/0
It/t-1
It/0
At/t-1
At/0
0
1
2
3
4
5
6
7
8
9
1987
810
10
0
0
8,10
1988
820
8
10
1,2346
1,2346
100,2346
101,2346
8,10
8,10
1989
828
2
18
0,9756
2,2222
100,9756
102,2222
8,20
8,10
1990
830
-8
20
0,2415
2,4691
100,2415
102,4691
8,28
8,10
1991
822
34
12
-0,9639
1,4815
99,0361
101,4815
8,30
8,10
1992
856
34
46
4,2363
5,6790
104,1363
105,6790
8,22
8,10
1993
890
34
80
3,9720
9,8765
103,9720
109,8765
8,56
8,10
1994
924
34
114
0,0382
14,0740
100,0382
114,0740
8,90
8,10
1995
929
5
119
0,5411
14,6914
100,5411
114,6914
9,24
8,10
4.Situatia stocului de marfa in anul 2000 la societatea comerciala "X" se prezinta in tabelul urmator :
Tabelul nr.16
Momentul
Inregistrarii
1 ian
1 feb
1 martie
1 aprilie
1 mai
1 iunie
Valoarea stocului
(mil.lei)
1100
1170
1160
1180
1190
1200
Momentul
Inregistrarii
1 iulie
1 aug
1 sept
1 oct
1 noemb
1 dec
Valoarea stocului
(mil.lei)
1090
1130
1050
1020
1070
1140
Precizati tipul seriei si determinati indicatorii medii ai acestei serii.
Rezolvare : Se constata ca inregistrarea valorii stocului de marfa s-a facut regulat la inceputul fiecarei luni, deci este o serie de momente cu intervale egale. Valoarea stocului mediu se determina folosind media cronologica simpla :
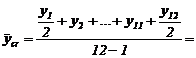
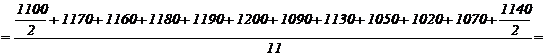
![]() mil.lei/luna.
mil.lei/luna.
Modificarea medie absoluta (sau sporul mediu) :
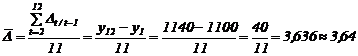 mil lei/luna
mil lei/luna
Indicele mediu de dinamica (sau indicele mediu lunar) :
![]()
Calculam logaritmul zecimal din I :

![]() 0,00141
0,00141
de unde ![]() antilog 0,00141 T
antilog 0,00141 T ![]() sau
sau ![]() %
%
Ritmul mediu lunar :
![]() sau %
sau %
5. Stocul unui grup omogen de marfuri a inregistrat urmatoarea evolutie in semestrul I al anului 2001 :
Tabelul nr.17
Momentul inregistrarii
1 I
15 II
1IV
1 V
31 VI
Valoarea stocului (mil.lei)
1700
1900
1800
1600
1550
Precizati tipul seriei si determinati nivelul mediu al seriei.
Rezolvare:
Seria prezentata este o serie de momente cu intervale neegale. Pentru usurinta rezolvarii vom considera luna egala cu 30 de zile.
Nivelul mediu se va calcula folosind media cronologica ponderata.
1I1II 15II 1III1IV 1V 31VI
t1 s 45 zilet2 s 45 zile t3 s 30 zile t4 s 60 zile
Deci  mil.lei/luna.
mil.lei/luna.
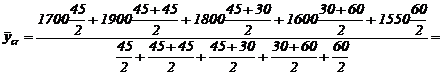
![]() 1720,83 1720,8
mil.lei/luna.
1720,83 1720,8
mil.lei/luna.
6. Valoarea vanzarilor de marfuri alimentare in 2000 a fost de 1580 mld.lei, iar dinamica acestora in fiecare an fata de 1994 a inregistrat urmatoarele valori :
Tabelul nr.18
Anul
1995
1996
1997
1998
1999
2000
Dinamica vanzarilor 1994s100%
129,85
136,915
138,45
138,52
140,20
139,15
N.E. Date conventionale
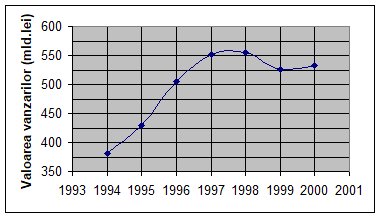
Sa se reconstituie seria de valori absolute si sa se reprezinte grafic aceasta.
Rezolvare:
Dinamica vanzarilor fata de 1994 reprezinta indicii de dinamica cu baza fixa y1994sy0:
![]() T I1/0 s
1,2985 T y1 s y0 1,2985
T I1/0 s
1,2985 T y1 s y0 1,2985
![]() T I2/0 s
1,36915 T y2 s y0 1,36915
T I2/0 s
1,36915 T y2 s y0 1,36915
![]()
![]() T I6/0 s
1,3915 T y6 s y0 1,3915 T 1580 s
y0 1,3915 T
T I6/0 s
1,3915 T y6 s y0 1,3915 T 1580 s
y0 1,3915 T
![]() mld.lei s 1135,46 1135,5
mld.lei
mld.lei s 1135,46 1135,5
mld.lei
Cu ajutorul lui y0 s 1135,5 mld.lei se vor obtine valorile vanzarilor de marfuri pentru fiecare an :
y1 s y1995 s 1135,5 1,2985 s 1474,44 1474,4 mld.lei.
y2 s y1996 s 1135,5 1,3915 s 1554,66 1554,7 mld.lei
y3 s y1997 s 1135,5 1,3845 s 1572,09 1572,1 mld.lei.
y4 s y1998 s 1135,5 1,3852 s 1572,89 1572,9 mld.lei.
y5 s y1999 s 1135,5 1,4020 s 1591,97 1592,0 mld.lei.
Seria reconstituita este :
Tabelul nr.19
Anul
1994
1995
1996
1997
1998
1999
2000
Valoarea vanzarilor (mld.lei)
1135,5
1474,4
1554,7
1572,1
1572,9
1592,0
1580,0
Graficul seriei este :
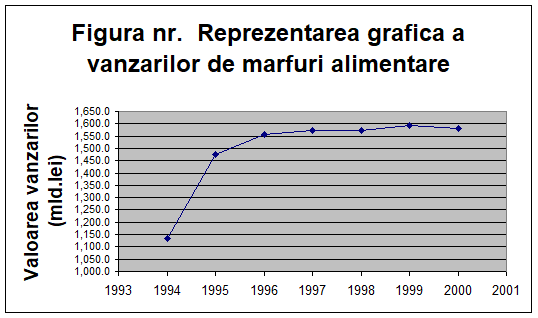
Fig.nr.Reprezentarea grafica a vanzarilor de marfuri alimentare.
7. In anul 2000 vanzarile de marfuri alimentare au fost mai mari fata de 1994 cu 39,848%, iar modificarile absolute in fiecare an fata de 1994 sunt prezentate in tabelul nr. 20.
Tabelul nr. 20
Anul
1995
1996
1997
1998
1999
2000
Modificari absolute (mld.lei)
48
125
170
174
145
152
Reconstituiti seria valorilor absolute si utilizati un procedeu mecanic si unul analitic pentru ajustarea valorilor seriei reconstituite. (Justificati alegerea modelului de ajustare).
Rezolvare:
Vanzarile de marfuri alimentare
fiind in anul 2000 mai mari fata de 1994 cu 39,848% inseamna ca se cunoaste
ritmul de dinamica R2000/1994s 39,848% T I2000/1994 % s 139,848% T I2000/1994s 1,39848. T ![]() 1,39848. Baza de comparatie fiind anul 1994 T y1994 s
y0 si apoi y1995 s y1,,y2000 s y6, deci
1,39848. Baza de comparatie fiind anul 1994 T y1994 s
y0 si apoi y1995 s y1,,y2000 s y6, deci ![]() 1,39848. Din tabelul nr. 20 avem
1,39848. Din tabelul nr. 20 avem
D2000/1994 s 152 mld.lei T y6 - y0 s152. Formam un sistem de ecuatii din care determinam yk, k s 0, 1,, 6 si vom exprima valorile lor cu numere intregi.
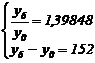 T
T ![]() T
T ![]() T y0 s y1994 381
mld.lei T y6 s 1,39848 381 s
532,8 533
mld.lei. Folosind modificarile absolute fata de 1994 obtinem :
T y0 s y1994 381
mld.lei T y6 s 1,39848 381 s
532,8 533
mld.lei. Folosind modificarile absolute fata de 1994 obtinem :
y1995 s y1994 +48 T y1995 s 381 + 48 s 429 mld.lei,
y1996 s y1994 + 125 T y1996 s 381 + 125 s 506 mld.lei,
y1997 s y1994 + 170 T y1997 s 381 + 170 s 551 mld.lei,
y1998 s y1994 + 174 T y1998 s 381 + 174 s 555 mld.lei,
y1999 s y1994 + 145 T y1999 s 381 + 145 s 526 mld.lei,
y2000 s y1994 + 152 T y2000 s 381 + 152 s 533 mld.lei.
Fig.nr. Reprezentarea grafica a vanzarilor de marfuri alimentare.
Graficul sugereaza o evolutie parabolica sau exponentiala
si ca urmare vom
determina
diferentele absolute cu baza in lant si indicii de dinamica cu baza in lant
(vezi tabelul nr.21).
Tabelul nr. 21
Anul
![]()
![]()
![]()
![]()
0
1
2
3
4
1994
381
1995
429
48
1,13
1996
506
77
29
1,18
1997
551
45
-32
1,09
1998
555
49
4
1,01
1999
526
-29
-78
0,95
2000
533
7
36
1,01
Diferentele absolute cu baza in lant de ordinul 2, dupa cum se observa in tabelul nr. 21 coloana 3, nu au valori aproape constante deci nu putem utiliza un polinom de gradul doi pentru ajustarea valorilor seriei cronologice.
Se observa ca valorile indicilor de dinamica cu baza in lant (vezi tabelul nr.21 coloana 4) au valori apropiate, deci se justifica alegerea modelului exponential ca model analitic si metoda indicelui mediu de dinamica ca procedeu mecanic.
Ecuatia modelului exponential
este: ![]() i s 0, 1,,6.
i s 0, 1,,6.
Prin logaritmare obtinem: ![]()
Sistemul de ecuatii normale
este: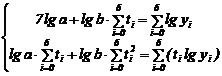
Calculul valorilor ajustate prin cele doua procedee. Tabelul nr.22.
Anul
![]()
Procedeul mecanic
![]()
![]()
![]()
![]()
0
1
2
3
4
5
1994
381
0
381
0
0
1995
429
1
403,86
25,14
632,0196
1996
506
2
428,0916
77,9084
6069,7187
1997
551
3
453,7771
97,2229
9452,2931
1998
555
4
481,0037
73,9963
5475,4492
1999
526
5
509,8639
16,1361
260,3727
2000
533
6
540,4558
7,4558
55,5887
Total
3481
3198,0521
282,9479
21945,4416
Tabelul nr.22. Continuare
Procedeul analitic
![]()
![]()
![]()
![]()
![]()
![]()
![]()
6
7
8
9
10
11
12
-3
9
2,5809
-7,7428
414,04
33,04
1091,6416
-2
4
2,6325
-5,2649
438,88
9,88
97,6144
-1
1
2,7042
-2,7042
465,22
40,78
1663,0084
0
0
2,7412
0
493,13
57,87
3348,9369
1
1
2,7443
2,7443
522,72
32,28
1041,9984
2
4
2,7210
5,4420
554,08
28,08
788,4864
3
9
2,7267
8,1802
587,33
54,33
2951,7489
0
28
18,8507
0,6546
3475,40
256,26
10983,4350
Folosind datele din tabelul nr.22 sistemul de ecuatii normale devine :
![]() T
T 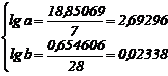 T
T
a s 102,69296 T a s 493,128
b s 100,02338 T b s 1,05531
Alegem o exprimare cu doua cifre dupa virgula, deci a s 493,13 si b s
1,06, asadar ecuatia modelului exponential este ![]() mld.lei, i s 0,
1,,6. Valorile ajustate sunt :
mld.lei, i s 0,
1,,6. Valorile ajustate sunt :
![]() s 493,13 1,06-3 s
414,04
s 493,13 1,06-3 s
414,04
![]() s 493,13 1,06-2 s
438,88
s 493,13 1,06-2 s
438,88
![]() s 493,13 1,06-1 s
465,22
s 493,13 1,06-1 s
465,22
![]() s 493,13 1,060 s
493,13
s 493,13 1,060 s
493,13
![]() s 493,13 1,061 s
522,72
s 493,13 1,061 s
522,72
![]() s 493,13 1,062 s
554,08
s 493,13 1,062 s
554,08
![]() s 493,13 1,063 s
587,33.
s 493,13 1,063 s
587,33.
Prin procedeul mecanic definim valorile ajustate ![]() prin
prin ![]() mld.lei, valori care sunt prezentate in tabelul nr.22 coloana
3.
mld.lei, valori care sunt prezentate in tabelul nr.22 coloana
3.
8. Valoarea absoluta a 1% din ritmul de crestere in 1995 fata de 1994 a fost de 3,81 mld.lei, modificarile relative in fiecare an in perioada 1995 - 2000 fata de anul anterior sunt prezentate in tabelul nr. 23.
Tabelul nr.23
Anul
1995
1996
1997
1998
1999
2000
Ritmul de crestere (scadere)%
12,598
17,949
8,893
0,7![]() 26
26
-5,225
1,331
Sa se reconstitue seria de date privind valoarea vanzarilor de marfuri alimentare intre anii 1995 - 2000.
Rezolvare:
Deoarece valoarea absoluta a 1% din ritmul de crestere in 1995 fata de 1994 a fost de 3,81 mld.lei deducem ca:
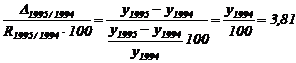 T
T ![]() mld.lei
mld.lei
Din tabelul nr.23 se observa ca R1995/1994% s 12,598 T
![]() T
T ![]() 0,12598 T y1995 s
1,12598 y1994 T
0,12598 T y1995 s
1,12598 y1994 T
y1995 s 1,12598 381 s 428,99838 429 mld.lei.
Analog se obtin valorile :
Y1996 s (1 + 0,17949) y1995 s 506 mld.lei
Y1997 s (1 + 0,08893) y1996 s 551 mld.lei
Y1998 s (1 + 0,00726) y1997 s 555 mld.lei
Y1999 s (1 - 0,05225) y1998 s 526 mld.lei
Y2000 s (1 + 0,01331) y1999 s 533 mld.lei
9. Ritmul mediu de crestere al vanzarilor de marfuri alimentare a fost de 5,75% in perioada 1994 - 2000, iar modificarile absolute in fiecare an fata de 1994 au inregistrat valorile ce sunt prezentate in tabelul nr.24.
Tabelul nr.24
Anul
1995
1996
1997
1998
1999
2000
Modificari absolute
(mld.lei)
48
125
170
174
145
152
Sa se reconstituie seria valorilor absolute privind vanzarea marfurilor alimentare in fiecare an in perioada 1995 - 2000.
Rezolvare :
Se cunoaste ritmul mediu de crestere ![]() T
T ![]()
Dar![]() la care se adauga D2000/1994
s 152 mld.lei (din tabelul nr.24) si obtinem un sistem din care calculam y2000
si y1994 :
la care se adauga D2000/1994
s 152 mld.lei (din tabelul nr.24) si obtinem un sistem din care calculam y2000
si y1994 :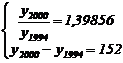 T
T
![]()
![]() T y1994 s
381,3 381
mld.lei si y2000 s 1,39856 381 s
532,8 533
mld.lei
T y1994 s
381,3 381
mld.lei si y2000 s 1,39856 381 s
532,8 533
mld.lei
Din : D1995/1994 s 48 mld.lei T y1995 s 48 + y1994 s 429 mld.lei
D1996/1994 s 125 mld.lei T y1996 s 125 + y1994 s 506 mld.lei
D1997/1994 s 170 mld.lei T y1997 s 170 + y1994 s 551 mld.lei
D1998/1994 s 174 mld.lei T y1998 s 174 + y1994 s 555 mld.lei
D1999/1994 s 145 mld.lei T y1999 s 145 + y1994 s 526 mld.lei
10. Valoarea vanzarilor de marfuri in judetul "X" a fost in anul 2001 cu 187 mld.lei mai mare fata de anul 1994, ceea ce reprezinta o crestere relativa cu 38,975%. Determinati valoarea vanzarilor de marfuri in anii 1994 si 2001 si indicatorii medii ce caracterizeaza vanzarile de marfuri in perioada 1994-2001.
Rezolvare : Cunoastem
modificarea absoluta a vanzarilor din anul 2001 fata de anul 1994 :D2001/1994
s 187 mld.lei T y2001 y1994
187 mld.lei si cresterea relativa cu 38,975% adica R2001/1994% s 38,975 T
R2001/1994 s 0,38975 T ![]() 0,38975 T
0,38975 T ![]() T y1994 s
479,79 479,8
mld.lei.
T y1994 s
479,79 479,8
mld.lei.
Dar y2001 s 187 + y1994 s 187 + 479,8 s 666,8 mld.lei.
Deci valoarea vanzarilor de marfuri in anul 1994 este y1994 s 479,8 mld.lei iar in anul 2001 este y2001 s 666,8 mld.lei.
Indicatorii medii ce pot fi determinati folosind nivelul absolut y1994 si y2001 sunt:
sporul mediu (![]() ) :
) :
![]()
![]() 26,71 26,7
mld.lei.
26,71 26,7
mld.lei.
Indicele mediu de crestere (![]() ) :
) :
![]()
![]()
![]()
![]() 1,04814 1,0481
sau
1,04814 1,0481
sau ![]() % s 104,81%.
% s 104,81%.
ritmul
mediu de crestere (![]() ) :
) :
![]() 1,0481 - 1 s 0,0481 sau
1,0481 - 1 s 0,0481 sau ![]() 104,81 - 100 s 4,81%.
104,81 - 100 s 4,81%.
PROBLEME PROPUSE
1. Pretul unui produs de panificatie a inregistrat urmatoarea evolutie in ultimii ani:
Tabelul nr.25
Anul
1994
1995
1996
1997
1998
1999
2000
2001
Pretul (lei)
120
150
250
380
590
1000
1200
1350
Se cere:
a) sa se reprezinte grafic seria cronologica,
b) sa se calculeze indicatorii absoluti, relativi si medii ce caracterizeaza seria cronologica,
c) folosind metode mecanice si analitice sa se ajusteze seria cronologica,
d) alegeti metoda cea mai buna care ajusteaza tendinta de evolutie a fenomenului.
2. Se cunosc urmatoarele date privind populatia ocupata (total) a Romaniei:
Tabelul nr.26
Anul
1991
1992
1993
1994
1995
1996
1997
1998
1999
Modificarea absoluta fata de 1990 (mii persoane)
-54
-382
-778
-899
-347
-1461
-1817
-2027
-2420
Se cere:
a) sa se reconstitue seria valorilor absolute stiind ca ritmul mediu de crestere a fost de -2,768% in perioada 1990-1999,
b) sa se reprezinte grafic seria,
c) sa se calculeze indicatorii medii,
d) sa se ajusteze seria printr-o metoda analitica si sa se calculeze coeficientul de variatie.
3. Dinamica consumului mediu anual de lapte si produse lactate din Romania a inregistrat urmatoarea evolutie prezentata in tabelul nr.27.
Tabelul nr.27
Anul
1991
1992
1993
1994
1995
1996
1997
1998
Dinamica fata de anul precedent
%
116,56
100,24
108,06
101,47
105,07
102,17
99,84
101,04
Stiind ca consumul mediu anual de lapte si produse lactate (l/locuitor) in anul 1994 a fost de 179,5 l se cere:
a) sa se reconstitue seria de date;
b) sa se calculeze toti indicatorii absoluti, relativi si medii;
c) sa se ajusteze seria folosind procedee mecanice;
d) sa se aleaga modelul cel mai bun de ajustare si sa se extrapoleze seria pentru anii 1999, 2000 si 2001.
4. Veniturile unei societati comerciale in perioada 1994-2001 se prezinta prin "cresterea fata de anul precedent" in tabelul nr.28.
Tabelul nr.28
Anul
1995
1996
1997
1998
1999
2000
2001
Cresterea fata de anul precedent (mil.lei)
50
32
55
46
52
52
57
Se cere:
a) sa se reconstitue seria de valori absolute stiind ca valoarea veniturilor a crescut in anul 1997 fata de anul 1994 cu 26,24%;
b) sa se calculeze indicatorii medii si sa se comenteze rezultatele;
c) folosind un procedeu mecanic si unul analitic sa se ajusteze seria cronologica, justificand procedeul ales;
d) sa se precizeze care din cele doua modele de ajustare caracterizeaza cel mai bine evolutia veniturilor in perioada analizata.
5. Consumul mediu pe familie pentru produsul "X" din judetul "Y" a inregistrat urmatoarea evolutie prezentata in tabelul nr.29.
Tabelul nr.29
Anul
1994
1995
1996
1997
1998
1999
2000
2001
Consumul mediu
(kg)
202
207
219
221
227
238
241
258
Se cere:
a) sa se reprezinte grafic seria cronologica;
b) sa se calculeze indicatorii ce caracterizeaza evolutia consumului mediu pe familie;
c) sa se ajusteze seria folosind metode mecanice si sa se aleaga cel mai bun model;
d) sa se estimeze consumul mediu pe familie pentru anii 2001 si 2003.
6. In semestrul II al anului 2001, stocul de marfuri inregistrat la un magazin alimentar este prezentat in tabelul nr.30.
Tabelul nr.30
Momentul
Inregistrarii
1VII
10VIII
5X
15XI
31XII
Valoarea stocului
(mil.lei)
78
62
69
83
70
Precizati tipul seriei si calculati nivelul mediu al seriei.
7. Stocurile de marfa la societatea comerciala "X" au inregistrat in cursul anului 2000 urmatoarele valori prezentate in tabelul nr.31.
Tabelul nr.31
Momentul
inregistrarii
1I
1II
1III
1IV
1V
1VI
Valoarea stocului
(mil.lei)
140
160
200
210
200
360
Continuare tabelul nr.31
Momentul
Inregistrarii
1VII
1VIII
1IX
1X
1XI
1XII
Valoarea stocului
(mil.lei)
320
250
190
185
155
142
Se cere:
a) Sa se precizeze tipul seriei;
b) Sa se calculeze indicatorii medii ai acestei serii.