|
|
|
ANALIZA FLUXURILOR DE SOSIRE SI SERVIRE A CALATORILOR
1 Analiza fluxului de sosire a calatorilor
Variabila aleatoare discreta asociata sosirii calatorilor in agentie este de forma:
,
i=0,1,2, ,
unde:
|
xi |
este |
numarul calatorilor sositi in agentie in unitatea de timp; |
|
pi |
|
probabilitatea sosirii in agentie a xi calatori in unitatea de timp. |
Probabilitatea pi (densitatea de probabilitate) se calculeaza cu relatia:
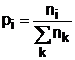, (1)
unde ni sunt frecventele empirice ale sosirii calatorilor in agentie in unitatea de timp (vezi tab. 1.1).
Functia de repartitie a variabilei aleatoare este:
. (2)
Valoarea medie a repartitiei corespunzatoare fluxului sosirilor este:
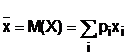. (3)
Dispersia de selectie a repartitiei sosirii calatorilor este:
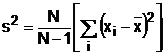, (4)
unde N reprezinta marimea esantionului analizat.
Cu ajutorul relatiilor de mai sus vom intocmi urmatorul tabel:
Tab.1:Determinarea densitatii de probabilitate si a functiei de repartitie corespunzatoare fluxului sosirii calatorilor in agentie:
xi
ni
pi
Φi
(xi-)2*fi
s2
0
1
0.001001
0.001001
0
0.08041512
8.80524
1
1
0.001001
0.002002
0.001001
0.06347225
2
5
0.005005
0.007007
0.01001
0.24265692
3
15
0.015015
0.022022
0.045045
0.5338878
4
34
0.034034
0.056056
0.136136
0.83829234
5
61
0.061061
0.117117
0.305305
0.95896857
6
91
0.091091
0.208208
0.546547
0.79970231
7
117
0.117117
0.325325
0.81982
0.45127844
8
132
0.132132
0.457457
1.057057
0.12252582
9
132
0.132132
0.58959
1.189189
0.00018125
10
119
0.119119
0.708709
1.191191
0.12810616
11
97
0.097097
0.805806
1.068068
0.40290634
12
73
0.073073
0.878879
0.876877
0.67399636
13
50
0.05005
0.928929
0.650651
0.8156991
14
32
0.032032
0.960961
0.448448
0.81270846
15
19
0.019019
0.97998
0.285285
0.69316367
16
11
0.011011
0.990991
0.176176
0.54526406
17
6
0.006006
0.996997
0.102102
0.38795174
18
3
0.003003
1
0.054054
0.24524936
∑
999
1
8.962963
8.79642606
2 Determinarea repartitiei teoretice corespunzatoare repartitiei empirice a sosirii calatorilor
Daca din calculele anterioare se
observa ca 
, rezulta ca repartitia empirica poate fi
asimilata cu o repartitie teoretica de tip Poisson cu media 
.
In cazul repartitiei Poisson, densitatea de probabilitate este data de relatia:
, k=0,1,2, (5)
unde P(k) reprezinta probabilitatea sosirii in agentie a k calatori in unitatea de timp.
Functia de repartitie corespunzatoare este:
. (6)
Frecventele teoretice ale sosirii calatorilor in agentie se determina cu relatia:
, k=0,1,2, (7)
Verificarea concordantei dintre
repartitia empirica si repartitia teoretica a sosirii
calatorilor in agentie se realizeaza cu ajutorul testului 
. Parametrul estimat in cadrul testului de
concordanta este media repartitiei . Functia are o repartitie
caracterizata prin numarul gradelor de libertate (f):
f=n-k-1,
unde:
|
n |
este |
numarul frecventelor empirice observate (n=19); |
|
k |
|
numarul parametrilor repartitiei teoretice estimati (k=1). |
f=19-1-1=17;
Valoarea 
se calculeaza cu
relatia:
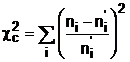. (8)
Cu ajutorul relatiilor de mai sus vom intocmi urmatorul tabel:
Tab. Determinarea densitatii de probabilitate si a functiei de repartitie corespunzatoare repartitiei Poisson:
P(k)
F(x)
nk'
((ni-ni')/ni')2
χc2
0.000128
0.000128
0.127938
46.46161403
56.94631
0.001148
0.001276
1.274643
0.046425922
0.005144
0.00642
6.413581
0.048578056
0.015369
0.021789
21.76695
0.096647529
0.034437
0.056226
56.16987
0.155782775
0.061732
0.117958
117.8403
0.232661726
0.092217
0.210175
209.9652
0.321029797
0.118077
0.328252
327.9242
0.413719342
0.13229
0.460542
460.0818
0.508503802
0.131746
0.592288
591.6957
0.603592791
0.118083
0.710371
709.6607
0.692746962
0.096216
0.806587
805.7803
0.773730972
0.071865
0.878452
877.5733
0.840551701
0.049548
0.928
927.0717
0.89504227
0.031721
0.959721
958.7611
0.93436117
0.018954
0.978675
977.6965
0.96151079
0.010618
0.989293
988.3038
0.97786352
0.005598
0.994891
993.8963
0.98796275
0.002788
0.997679
996.6811
0.99398908
Pentru f=17 grade de libertate vom
avea ca 
Cu ajutorul tabelelor 1. si se va intocmi reprezentarea grafica a densitatii de probabilitate si a functiei de repartitie atat pentru repartitia empirica cat si pentru cea teoretica:
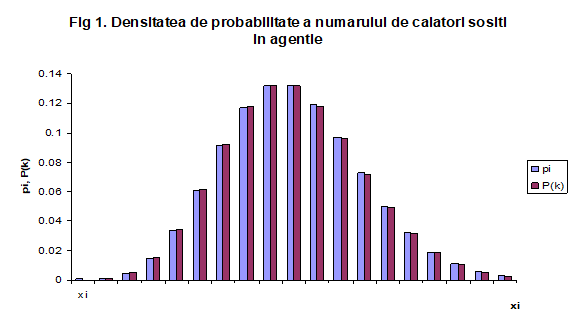
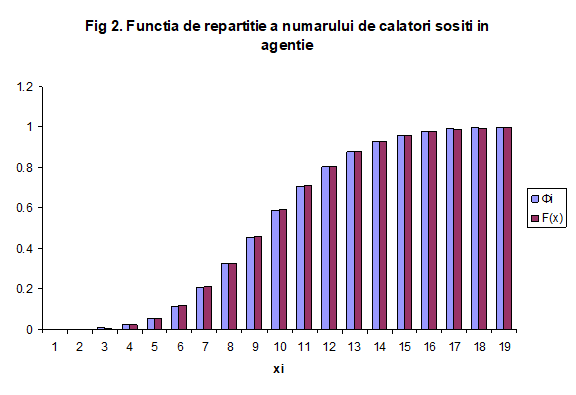
3 Analiza fluxului de servire a calatorilor
Conform temei proiectului, duratele de servire a calatorilor au o repartitie exponential-negativa. Aceasta se caracterizeaza prin densitatea de probabilitate :
, t >0 (9)
si prin functia de repartitie:
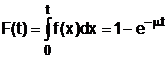, t>0, (10)
unde 
este intensitatea
medie a servirilor.
Timpul mediu de servire a unui calator este 
[min].
Intensitatea medie a servirilor este 
[cal./min].
Pentru 
si 
Cu ajutorul relatiilor de mai sus vom intocmi urmatorul tabel:
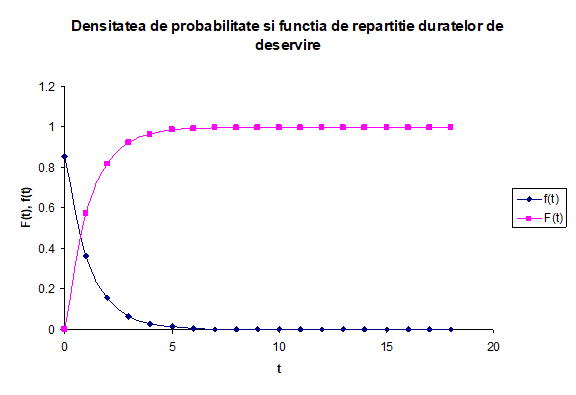
Tab.3 Determinarea densitatii de probabilitate si a functiei de repartitie corespunzatoare duratelor de servire a calatorilor:
t
f(t)
F(t)
μ=
0
0.857143
0
0.857143
1
0.363748
0.575627
ts (med) =
2
0.154365
0.819908
1.166667
3
0.065508
0.923574
4
0.0278
0.967567
5
0.011798
0.986236
6
0.005007
0.994159
7
0.002125
0.997521
8
0.000902
0.998948
9
0.000383
0.999554
10
0.000162
0.999811
11
6.89E-05
0.99992
12
92E-05
0.999966
13
1.24E-05
0.999986
14
5.27E-06
0.999994
15
23E-06
0.999997
16
9.48E-07
0.999999
17
4.02E-07
1
18
1.71E-07
1
Cu ajutorul tabelului de mai sus se va intocmi reprezentarea grafica a densitatii de probabilitate si a functiei de repartitie a duratelor de servire a calatorilor:
