
|
|
|
UNIVERSITATEA TEHNICA DE CONSTRUCTII BUCURESTI
FACULTATEA DE GEODEZIE
GEODEZIE MATEMATICA III:
"INDESIREA RETELELOR GEODEZICE PLANIMETRICE"
TEMA
Se considera reteaua planimetrica formata din 4 puncte vechi in care s-au efectuat observatii azimutale in toate combinatiile si vize reciproce precum si 2 puncte noi de indesire catre si dinspre care s-au efectuat observatii azimutale.

Se dau:
Coordonatele planimetrice ale punctelor vechi din retea A, B, C, D;
Directiile masurate, compensate in statie, reduse la planu de proiectie;
Distantele A-1, 1-2, 2-C reduse la planul proiectiei.
Se cere:
Sa se efectueze prelucrarea datelor respective prin metoda observatiilor indirecte in urmatoarele situatii:
a) Directii orizontale de aceasi precizie fara distanta (fiecare masuratoare are aceeasi pondere 0.5);
b) Directii orizontale de preizii diferite in functie de abaterea standard calculata in fiecare statie, fara distante;
c) Directii orizontale de precizii diferite si distante masurate cu un instrument caracterizat de coeficientii a si b, avand valorile: a=2 mm, b=1,5 mm/km;
d) Directii orizontale de precizii diferite si distante masurate cu un instrument caracterizat cu coeficientii a si b, avand valorile: a=40 mm, b=10 mm/km;
e) Considerandu-se datele initiale anterioare sa se determine coordonatele punctului 1 de indesire prin metoda intersectiei multiple inainte avand ca puncte vechi punctele A, B, C, D;
f) Considerandu-se datele initiale anterioare sa se determine coordonatele punctului 2 de indesire prin metoda intersectiei multiple inapoi, avand la dispozitie punctele vechi A, B, C, D si coordonatele punctului 1 de la punctul e).
DATELE INITIALE
Pct.
N [m]
E [m]
A
143961.628
271411.057
B
149312.154
266950.471
C
155043.181
272442.630
D
148138.017
277580.447
Valori masurate reduse la planul de peoiectie
(Directii orizontale)
PS
PV
Dir. [ g c cc ]
A
B
242.23525
2
281.64866
C
292.38542
1
328.41316
D
348.59122
B
C
128.60227
2
157.33764
D
186.96093
1
194.01084
A
235.71660
C
D
270.76543
1
295.94922
A
317.39828
2
333.65657
B
360.13421
D
A
206.42134
1
235.29033
B
251.30990
2
268.22028
C
303.58273
1
A
130.29833
B
202.41513
2
235.63217
C
272.82134
D
379.34542
2
A
260.97698
B
343.18513
C
87.97185
D
189.71863
1
213.07558
Distante masurate si reduse la planul de proiectie
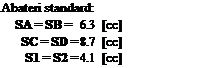
DA-1=4686,370m
D1-2=4596,230m
D2-C=4540,473m
MEMORIU TEHNIC
Reteaua geodezica:
este multimea punctelor care alcatuiesc o infrastructura, puncte care se gasesc pe suprafata pe care se desfasoara lucrarea si a caror pozitie este cunoscuta intr-un sistem unitar.
Reteaua geodezica planimetrica este o retea geodezica desfasurata in spatiul bidimensional, pozitia punctelor fiind data de un set de coordonate (x,y) sau (N,E). Prin masuratori planimetrice se determina pozitiile plane ale unor puncte care alcatuiesc reteaua respectiva, iar prin aceste puncte poate fi reprezentata suprafata de lucru.
Functie de natura elementelor masurate, retelele geodezice pot fi:
retele de triangulatie (in care sunt efectuate numai masuratori de directii unghiulare orizontale)
retele de trilateratie (in care se efectueaza numai masuratori de distante)
retele de triangulatie trilateratie (in care se efectueaza ambele tipuri de masuratori).
In acest proiect intalnim retele de triangulatie si de triangulatie-trilateratie astfel:
in primele doua cazuri si ultimele doua cazuri reteaua geodezica este de triangulatie,
in cazurile 3 si 4 reteaua geodezica este de triangulatie-trilateratie.
Numarul punctelor geodezice noi de ordinul III. este 2, deci sunt 4 necunoscute de determinat(X1,Y1,X2,Y2).
Numarul de masuratori si de necunoscute in cele 6 cazuri de compensare:
- In primele doua cazuri s-au efectuat masuratori de directii orizontale in fiecare punct atat spre puncte vechi cat si spre puncte noi, astfel rezultand 30 de masuratori de directii, iar numarul necunoscutelor este 4
- In cazurile 3 si 4 numarul masuratorilor creste cu 3, in afara de cele 30 de masuratori de directii fiind efectuate si trei masuratori de distanta, iar numarul necunoscutelor este 7.
In cazul 5 numarul masuratorilor este 16 (numai directii orizontale)
In ultimul caz numarul masuratorilor este 10 (numai directii orizontale) iar numarul necunoscutelor fiind 2.
In ultimele 2 cazuri de compensare pentru indesire retelelor geodezice se foloseste metoda intersectiei multiple inainte si inapoi:
In cazul intersectiei multiple inainte trebuie sa determinam coordonatele punctului1.Pentru determinarea riguroasa a coordonatelor punctului nou 1 sunt stationate alte puncte vechi (A,B,C,D) dintr-o retea geodezica planimetrica in care se fac observatii unghiulare orizontale atat catre punctul nou cat si catre alte puncte vechi din retea.
- Cazul intersectiei multiple inapoi consta in stationarea in punctul nou 2 ale carui coordonate vrem sa le determinam riguros si efectuarea observatiilor unghiulare orizontale catre alte puncte vechi din retea (A,B,C,D).
Masuratorile se prelucreaza in toate cele 6 cazuri cu metoda masuratorilor indirecte, prin care rezulta atat cresteri de coordonate ale punctelor noi, fata de coordonatele lor provizorii, cat si corectii ale masuratorilor.
Prelucrarea masuratorilor se face prin metoda masuratorilor indirecte
Metoda masuratorilor indirecte consta in parcurgerea urmatoarelor etape:
1. calculu elemetelor provizorii;
2. Transformarea ecuatiilor de corectii dupa regulile de echivalenta;
3. Formarea modelului functional-stohastic;
4. Normalizarea sistemului de ecuatii liniare ale corectiilor si rezolvarea sistemului normal de ecuatii;
5. Calculul elementelor compensate si controlul compensarii;
6. Estimarea preciziei si calcule ale elementelor elipsei
SCOP: Determinarea coordonatelor pentru cele 2 puncte noi ale retelei (valorile cele mai probabile) si preciziile cu care au fost determinate acestea.
1.) Calculul elementelor provizorii:
a. Calculul distantelor si orientarilor intre punctele vechi:
![]()
![]()
![]()
b. Orientarea statiilor cu coordonate cunoscute:
Consta in determinarea unui unghi de orientare mediu sau mediu ponderat, fiind luata ca ponderi distantele dintre puncte exprimate in km.
Folosim urmatoarele relatii de calcul:
![]()
![]()

ZSi - unghiul de orientare al statiei S dat de directia catre punctul vechi i;
ZS - unghiul de orientare al statiei S;
DSi - distanta de la statia S pana la punctual i;
θSi - orientarea din statia S catre punctele noi i;
- cu * notand elementele masurate.
c. Calculul coordonatelor provizorii (ale punctelor noi)
Consta in calculul unor coordonate pentru punctele noi, care urmeaza a fi compensate, folosind coordonatele punctelor vechi respective orientarilor laturilor dintre punctele vechi
Se realizeaza prin metoda intersectiei inainte din doua combinatii, folosind urmatoarele relatii:
![]()
![]()
Notand cu 1 parametrii punctului nou;
Se face media valorilor din cele doua combinatii.
d. Calculul coeficientilor de directie (necesar determinarii variatiei orientarii functie de coord. plane)
Variatia orientarii:
ij=0ij+dij
x+α==0ij+dij
zSo+dz+ α*+vij=0ij+dij
dij= aij * dNj + bij * dEj - aij * dNi - bij * dEi
Calculul coeficientilor consta in calculul coeficientilor pentru coordonate relative corespunzatori fiecarei ecuatii de corectie folosind relatiile:
- pentru directii unghiulare:
![]() [a]=cc/dm[b]=cc/dm
[a]=cc/dm[b]=cc/dm
![]()
- pentru distante:
![]()
unde:
![]()
![]()
![]()
ρCC = 636620
a -este coeficientul pentru variatiile pe ordonata ON;
b -este coeficientul pentru variatiile pe abscisa OE;
Calculele pot fi verificate calculand raportul dintre a si b si comparandu-l cu tangenta orientarii laturii:
![]()
![]()
Regula stbilirii semnului coeficientilor:
Pentru stabilirea semnului coeficientilor de directie de la un punct vechi la un punct nou la orientarea laturii dintre cele doua puncte, se adauga 100g (in fucnctie de cadran) iar semnul lui a este pe directia N si semnul lui b pe directia E
In cazul stabilirii coeficientilor de directie de la un punct nou la un punct vechi , din orientarea initiala se scade 100g, iar semnul lui a este de pe directia X si semnul lui b de pe directia E
e. Calculul variatiei distantelor functie de variatia coordonatelor plane (in cazul compensarilor 3 si 4):
Dij = DijO + dDij
dDij= + AijdNj + BijdEj - AijdNi -BijdEi ;
unde: Aij= cos Oij si Bij= sin Oij
f. Forme ale ecuatiei de corectie la prelucrarea observatiilor efectuate in retele geodezice
1. Directii azimutale centrate, reduse si reduse la planul de proiectie
Consideram un punct de statie S in care s-au efectuat observatii unghiulare orizontale catre alte n puncte din retea .
Prin procesul de masurare aceste valori vor primi niste corectii si se vor obtine astfel valorile cele mai probabile.
si=*si+vsi
In punctul de statie S cunoastem valorile provizorii ale orientarilor catre alte puncte vizate, astfel ca putem calcula valori pentru unghiul mediu de orientare.
zis=0si-0si
Prin medierea acestor valori se obtin o valoare provizorie pentru unghiul de orientare al statiei S.
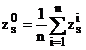
In urma prelucrarii unghiul mediu provizoriu va primi o corectie dzs , astfel putem calcula valoarea cea mai probabila a unghiului de orientare in statia S.
zs=zos+dzs
Ecuatia de corectie pentru o directie azimutala este sub forma :
vij=
-dzi + aijdxj + bijdyj -
aij* dxi - bij* dyi + lijunde: lij=zis-z0i![]() iar intr-o statie [ l ] = 0
iar intr-o statie [ l ] = 0
5
Cazul intersectiei multiple inainte:-dz + aiP dxP + bipdyP +liP = ViP ; pi
Cazul intersectiei multiple inapoi: -dz + aPi dxp + bPidyP +lPi = VPi ; pi
2. Distante reduse la planul de proiectie
In urma procesului de prelucrare se obtin corectii care se aplica la valorile aproximative ale distantelor rezultand astfel valorile cele mai probabile al acestora.
Dij = Dij* + vijD
De asemenea in urma procesului de prelucrare datorita variatiei coordonatelor plane variaza si distanta cu o cantitate dD
Dij = DijO + dDij
In urma prelucrarii trebuie indeplinita conditia:
Dij* + vijD = DijO + dDij
Ecuatiei de corectie pentru distante este:
vDij= + Aijdxj + Bijdyj - Aijdxi -Bijdyi + lDij; unde: lDij= DijO - Dij*
2.)Transformarea ecuatiilor corectiilor dupa regulile de echivalenta
Forma generala a ecuatiilor este :
-dzi + aij dNj + bij dEj - aij dNi - bij dEi + lij = vij ; pij
Prin aplicarea regulilor de echivalenta se urmareste eliminarea din sistemul ecuatiilor de corectii a numarului de ecuatii si sa se elimine o parte din necunoscute. In geodezie sunt importante trei reguli de echivalenta:
Numarul initial al ecuatiilor corectiilor, scrise pentru directiile masurate , este egal cu numarul directiilor in cadrul retelei.
a) Prima regula de echivalenta:
- se aplica atunci cand in fiecare ecuatie din sistemul de ecuatii de corectii avem o necunoscuta cu acelas coeficient si consta in eliminarea acelei necunoscute, sistemul avand acum o necunoscuta mai putin, insa se mai adauga si o ecuatie in plus numita ecuatie suma de forma:
![]()
- dupa aplicarea primei reguli de echivalenta, din totalul de 30 ecuatii si 10 necunoscute ( dx1, dy1, dx2, dy2, dz de 6 ori ) mai raman 30 - 12 (ecuatiile scrise intre punctele vechi ) + 6 ( ecuatii suma ) = 24 ecuatii ramase si 4 necunuoscute (dx1, dy1, dx2, dy2 );
b) A doua regula de echivalenta:
- se refera la vize reciproce
- se aplica atunci cand toate necunoscutele din sistem au aceiasi coeficienti in toate ecuatiile din sistem:
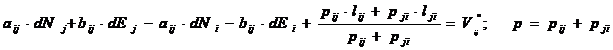
- dupa aplicarea celei de a-2-a reguli de echivalenta din cele 18 ecuatii cu vize reciproce raman doar 9 ecuatii la care se adauga cele 6 ecuatii suma, avand astfel un sistem cu 15 ecuatii si 4 necunoscute;
c) A treia regula de echivalenta:
- se aplica atunci cand se doreste aducerea ecuatiilor la
ponderea 1 sau -1 si se realizeaza prin inmultirea ecuatiei cu ![]() :
:
![]()
3.) Formarea modelului functional-stohastic:
Modelul functional:
V = AX + L (1) unde V - vectorul corectiilor
A - matricea coeficientilor sistemului de ecuatii ale corectilor
X - vectorul necunoscutelor
L - vectorul termenilor liber
Modelul stohastic:
Cm = ![]() Qm (2) unde Cm - reprezinta
matricea de varianta -covarianta
Qm (2) unde Cm - reprezinta
matricea de varianta -covarianta
Qm - matricea cofactorilor
- variatia unitatii de pondere
- La formarea modelului functional stohastic trebuie sa se aiba in vedere urmatoarele: prelucrarea riguroasa a masuratorilor , sa se raporteze la un sistem unitar.
-Orice modificare in modelul functional stohastic conduce la obtinerea altor rezultate.
-Conditia sub care se efectueaza prelucrarea prin metoda observatilor indirecte este conditia de minim sau conditia celor mai mici patrate:
[pvv]=minim sau VTPV = minim - mas ponderate
[vv]=minim sau VTV = minim - mas neponderate
Stabilirea ponderilor:
Ponderile pot fi determinate in functie de mai multi factori , cum ar fi : erorile medii de masurare, numarul de masuratori, prelucrari anterioare.
Pentru directii
azimutale: ![]()
Toate masuratorile dintr-o statie au aceeasi pondere.
4.) Rezolvarea sistemului normal
- prin tratare matriciala -
Se rezolcva prin metoda Gauss-Markov, in cazul masuratorilor indirecte:
N= AT * P * Aunde: A - reprezinta matricea coeficientilor sistemului de ecuatii
P - reprezinta matricea ponderilor
N - matricea sistemului normal
X = - N-1 * AT * P * Lunde: X - matricea necunoscutelor
L - matricea termenilor liberi
V=AX+L unde V-vectorul corectiilor
L -matricea termenilor liberi
5.) Calculul valorilor compensate ale necunoscutelor si a masuratorilor efectuate.
Controlul compensarii
a) Calculul valorilor celor mai probabile ale observatiilor unghiulare
si = *si+vsi
b) Calculul variatiilor orientarii si variatiilor distantelor functie de coordonatelor plane
dij = aijdxj + bijdyj - aij dxi - bijdyi
Verificare:[ V ] = 0 si [ lij
] = 0in fiecare statie; ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
c) Calculul corectiilor pentru unghiul de orientare
Pentru fiecare statie se calculeaza corectia unghiului de orientare provizoriu cu relatia:
![]()
d)Calculul valorilor cele mai probabile ale coordonatelor (compensarea coordonatelor):
Xi = X0i + dxi
Yi = Y0i + dyi
unde: i = 1,2
6.) Calculul preciziilor si al elementelor elipsei
Estimarea preciziilor:
a)abaterea standard a unitatii de pondere:
![]()
c) abaterea standard a necunoscutelor:
![]()
unde i = 1,2
![]()
d)abaterea standard de determinare a pozitiei punctului:
![]()
unde i = 1,2
e) abaterea standard pe retea:
![]()
unde n - numarul de puncte noi;
Elementelor elipsei:
![]()
![]()
unde:
a = semiaxa mare a elipsei,
![]() b=
semiaxa mica a elipsei,
b=
semiaxa mica a elipsei,
φ = orientarea semiaxei mari
TABELELE DE CALCUL
a. Calculul distantelor si a orientarilor punctelor de coord. cunoscute.
Tabel 1. Calculul distantelor si a orientarilor
Pct
N
E
Θ
D1
D2
D3
A
143961.628
271411.057
355.7588497
B
149312.154
266950.471
6965.98564
6965.98564
6965.98564
Δ
5350.526
-4460.586
A
143961.628
271411.057
5.9092134
C
155043.181
272442.630
11129.46359
11129.46359
11129.46359
Δ
11081.553
1031.573
A
143961.628
271411.057
62.1153712
D
148138.017
277580.447
7450.073694
7450.073694
7450.073694
Δ
4176.389
6169.390
B
149312.154
266950.471
48.6452587
C
155043.181
272442.630
7937.788165
7937.788165
7937.788165
Δ
5731.027
5492.159
B
149312.154
266950.471
107.0034123
D
148138.017
277580.447
10694.62423
10694.62423
10694.62423
Δ
-1174.137
10629.976
C
155043.181
272442.630
159.2763886
D
148138.017
277580.447
8606.88407
8606.88407
8606.88407
Δ
-6905.164
5137.817
b. Calculul unghiurilor de orientare al statiilor pct. de coord. cunoscute.
Tabel 2. Calculul unghiului de orientare al statiei.
Statie
Punct
Ө
Dir masurate
z
pondere
z0
B
355.7588497
242.23525
113.5235997
6.9660
A
C
5.9092134
292.38542
113.5237934
11.1295
113.5238449
D
62.1153712
348.59122
113.5241512
7.4501
C
48.6452587
128.60227
320.0429887
7.9378
B
D
107.0034123
186.96093
320.0424823
10.6946
320.0425760
A
155.7588497
235.71660
320.0422497
6.9660
D
159.2763886
270.76543
288.5109586
8.6069
C
A
205.9092134
317.39828
288.5109334
11.1295
288.5109743
B
248.6452587
360.13421
288.5110487
7.9378
A
262.1153712
206.42134
55.6940312
7.4501
D
B
307.0034123
251.30990
55.6935123
10.6946
55.6937039
C
359.2763886
303.58273
55.6936586
8.6069
Tabel 3. Calculul orientarilor catre punctele noi
Statie
punct
Ө
A
1
41.9370049
2
395.1725049
B
1
114.0534160
2
77.3802160
C
1
184.4601943
2
222.1675443
D
1
290.9840339
2
323.9139839
c.Calculul coordonatelor provizorii pentru punctele noi
Tabel 4. Calculul coordonatelor provizorii pentru punctele1 si 2
Punct
N
E
Ө
tgӨ
A
143961.628
271411.057
41.9370049
0.774095826
1
147667.420
274279.6952
1
147667.420
274279.6952
B
149312.154
266950.471
114.0534160
-4.456176501
B
149312.154
266950.471
114.0534160
-4.456176501
1
147667.4248
274279.6745
1
147667.4248
274279.6745
C
155043.181
272442.630
184.4601943
-0.249065241
C
155043.181
272442.630
184.4601943
-0.249065241
1
147667.4036
274279.6798
1
147667.4036
274279.6798
D
148138.017
277580.447
290.9840339
7.013755950
D
148138.017
277580.447
290.9840339
7.013755950
1
147667.4041
274279.6828
1
147667.4041
274279.6828
A
143961.628
271411.057
41.9370049
0.774095826
Punct
N
E
Ө
tgӨ
A
143961.628
271411.057
395.1725049
-0.075975797
2
150775.208
270893.3898
2
150775.208
270893.3898
B
149312.154
266950.471
77.3802160
2.694992039
B
149312.154
266950.471
77.3802160
2.694992039
2
150775.1973
270893.3610
2
150775.1973
270893.3610
C
155043.181
272442.630
222.1675443
0.362997880
C
155043.181
272442.630
222.1675443
0.362997880
2
150775.1784
270893.3541
2
150775.1784
270893.3541
D
148138.017
277580.447
323.9139839
-2.535716180
D
148138.017
277580.447
323.9139839
-2.535716180
2
150775.163
270893.3932
2
150775.163
270893.3932
A
143961.628
271411.057
395.1725049
-0.075975797
Tabel 5. Coordonate provizorii
Punct
N
E
1
147667.4132
274279.6831
2
150775.1867
270893.3745
Tabel 6. calculul coeficientilor aij si bij
Pct
N
E
Ө
cos Ө
D ij
a ij
b ij
a ij/ b ij
tgӨ
sin Ө
b ij/a ij
A
143961.628
271411.057
41.9369323
0.790761811
4.686348188
-8.3154377
10.74215495
-0.774094001
TRUE
1
147667.413
274279.683
0.7740940
0.612123973
Δ
3705.785
2868.626
-1.291832774
TRUE
A
143961.628
271411.057
395.1723478
0.997126087
6.833196676
0.705823137
9.289801535
0.075978279
TRUE
2
150775.187
270893.375
-0.0759783
-0.075759924
Δ
6813.559
-517.682
13.1616563
TRUE
B
149312.154
266950.471
114.0534964
-0.218963247
7.511492661
-8.269610832
-1.855774724
4.456150159
TRUE
1
147667.413
274279.683
-4.4561502
0.975733107
Δ
-1644.741
7329.212
0.224408955
TRUE
B
149312.154
266950.471
77.3804380
0.347878439
4.205585913
-14.19199377
5.266005182
-2.695020851
TRUE
2
150775.187
270893.375
2.6950209
0.937539648
Δ
1463.033
3942.904
-0.371054643
TRUE
C
155043.181
272442.630
184.4601481
-0.970355372
7.601099589
-2.024180033
-8.127082535
0.249066012
TRUE
1
147667.413
274279.683
-0.2490660
0.241682542
Δ
-7375.768
1837.053
4.014999853
TRUE
C
155043.181
272442.630
222.1673146
-0.939987259
4.540481047
4.784092635
-13.17954381
-0.362993796
TRUE
2
150775.187
270893.375
0.3629938
-0.341209543
Δ
-4267.994
-1549.255
-2.754868022
TRUE
D
148138.017
277580.447
290.9842052
-0.141146856
3.334143136
18.90280533
-2.695052609
-7.013891034
TRUE
1
147667.413
274279.683
7.0138910
-0.989988669
Δ
-470.604
-3300.764
-0.142574214
TRUE
D
148138.017
277580.447
323.9141182
0.366869923
7.18829618
8.23880799
3.249125027
2.53570051
TRUE
2
150775.187
270893.375
-2.5357005
-0.93027225
Δ
2637.170
-6687.072
0.39436834
TRUE
1
147667.413
274279.683
347.2711723
0.676156905
4.596231234
10.20476633
9.365390622
1.089625274
TRUE
2
150775.187
270893.375
-1.0896253
-0.736757653
Δ
3107.773
-3386.309
0.9177467
TRUE
CALCULELE COMPENSARII
a) Directii orizontale de aceasi precizie fara distante
Sistemul linear al ecuatiilor de corectie
Ecuatie
P
Necunoscute
T L
dN1
dE1
dN2
dE2
v''A1
1
-8.3154377
10.74215495
0
0
-0.6960843983
v''A2
1
0
0
0.705823137
9.289801535
-0.9473381290
v''B1
1
-8.269610832
-1.855774724
0
0
-1.6251139564
v''B2
1
0
0
-14.19199377
5.266005182
0.1342096331
v''C1
1
-2.024180033
-8.127082535
0
0
0.5035670647
v''C2
1
0
0
4.784092635
-13.17954381
-0.7885875090
v''D1
1
18.90280533
-2.695052609
0
0
0.8223461143
v''D2
1
0
0
8.23880799
3.249125027
0.4951816427
v''12
1
-10.20476633
-9.365390622
10.20476633
9.365390622
2.1879926322
v'A
-0.4
-4.15771885
5.371077475
0.352911568
4.644900768
0
v'B
-0.4
-4.134805416
-0.927887362
-7.095996883
2.633002591
0
v'C
-0.4
-1.012090017
-4.063541268
2.392046317
-6.589771907
0
v'D
-0.4
9.451402666
-1.347526305
4.119403995
1.624562514
0
v'1
-0.4
-4.9555947797
-5.65057277
-5.102383163
-4.682695311
0
v'2
-0.4
-5.102383163
-4.682695311
4.8707481603
6.995389276
0
-8.3154377
10.74215495
0
0
0
0
0.705823137
9.289801535
-8.269610832
-1.855774724
0
0
0
0
-14.19199377
5.266005182
-2.024180033
-8.127082535
0
0
0
0
4.784092635
-13.17954381
A
18.90280533
-2.695052609
0
0
0
0
8.23880799
3.249125027
-10.20476633
-9.365390622
10.20476633
9.365390622
-4.15771885
5.371077475
0.352911568
4.644900768
-4.134805416
-0.927887362
-7.095996883
2.633002591
-1.012090017
-4.063541268
2.392046317
-6.589771907
9.451402666
-1.347526305
4.119403995
1.624562514
-4.9555947797
-5.65057277
-5.102383163
-4.682695311
-5.102383163
-4.682695311
4.8707481603
6.995389276
-0.6960843983
-0.9473381290
-1.6251139564
0.1342096331
0.5035670647
-0.7885875090
L
0.8223461143
0.4951816427
2.1879926322
0.0000000000
0.0000000000
0.0000000000
0.0000000000
0.0000000000
0.0000000000
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
P
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
-0.4
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
-0.4
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
-0.4
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
-0.4
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
-0.4
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
-0.4
532.952
-22.812
-130.065
-87.306
-22.812
239.103
-95.264
-104.029
N
-130.065
-95.264
347.643
-21.630
-87.306
-104.029
-21.630
327.825
0.00244031
0.001256
0.001328
0.001136
N^-1
0.001256217
0.00633
0.00236
0.002499
0.001327934
0.00236
0.004105
0.001373
0.001136158
0.002499
0.001373
0.004237
-0.042970633
0.075207016
X
-0.057268602
-0.065786085
Tabel cresteri de coordonate
dN1
-0.042970633
[dm]
dE1
0.075207016
[dm]
dN2
-0.057268602
[dm]
dE2
-0.065786085
[dm]
Tabel 7. Coordonatele punctelor noi
N
E
1
147667.409
274279.691
2
150775.181
270893.368
Calculul dij, dӨ
Pct. Statie
Pct. Vizat
aij
b ij
dӨ
dz
lij
vij
P
Pvv
A
B
0.1027287719
-2.0116902
-2.1144190209
0.5
2.235384
2
0.705823137
9.289801535
-0.6515611819
0.1027287719
-1.1307552
-1.8850451979
0.5
1.776698
C
0.1027287719
-0.0746293
-0.1773580369
0.5
0.015728
1
-8.3154377
10.74215495
1.1652050413
0.1027287719
-0.2859600
0.7765162869
0.5
0.301489
D
0.1027287719
3.5030347
3.4003059686
0.5
5.78104
∑
0.5136438595
0.0000000
B
C
0.1364217820
3.5365772
3.4001553866
0.5
5.780528
2
-14.19199377
5.266005182
0.4663257736
0.1364217820
1.6298703
1.9597742799
0.5
1.920358
D
0.1364217820
-1.5270010
-1.6634227603
0.5
1.383488
1
-8.269610832
-1.855774724
0.2157831363
0.1364217820
0.2140882
0.2934495836
0.5
0.043056
A
0.1364217820
-3.8535347
-3.9899564905
0.5
7.959876
∑
0.6821089099
0.0000000
C
D
0.0137637946
0.3595115
0.3457477365
0.5
0.059771
1
-2.024180033
-8.127082535
-0.5242333262
0.0137637946
0.0545264
-0.4834707653
0.5
0.116872
A
0.0137637946
0.1070405
0.0932766911
0.5
0.00435
2
4.784092635
-13.17954381
0.5930522994
0.0137637946
-1.7811697
-1.2018812442
0.5
0.722259
B
0.0137637946
1.2600914
1.2463275837
0.5
0.776666
∑
0.0688189732
0.0000000
D
A
-0.3401049226
2.4805460
2.8206508985
0.5
3.978036
1
18.90280533
-2.695052609
-1.0149523817
-0.3401049226
0.9212261
0.2463786883
0.5
0.030351
B
-0.3401049226
-2.7076453
-2.3675403612
0.5
2.802624
2
8.23880799
3.249125027
-0.6855722312
-0.3401049226
0.5505201
0.2050528362
0.5
0.021023
C
-0.3401049226
-1.2446470
-0.9045420619
0.5
0.409098
∑
-1.7005246129
0.0000000
1
A
8.3154377
-10.74215495
1.1652050413
-0.3249120851
-1.1062088
0.3839083124
0.5
0.073693
B
8.269610832
1.855774724
0.2157831363
-0.3249120851
-3.4643161
-2.9236209208
0.5
4.27378
2
10.20476633
9.365390622
-1.4663628951
-0.3249120851
2.8944511
1.7530002912
0.5
1.536505
C
2.024180033
8.127082535
-0.5242333262
-0.3249120851
0.9526078
0.7532865328
0.5
0.28372
D
-18.90280533
2.695052609
-1.0149523817
-0.3249120851
0.7234661
0.0334257844
0.5
0.000559
∑
-1.6245604254
0.0000000
2
A
-0.705823137
-9.289801535
-0.6515611819
-0.3488236471
-0.7639210
-1.0666585487
0.5
0.56888
B
14.19199377
-5.266005182
0.4663257736
-0.3488236471
-1.3614510
-0.5463016014
0.5
0.149223
C
-4.784092635
13.17954381
0.5930522994
-0.3488236471
0.2039947
1.1458706774
0.5
0.65651
D
-8.23880799
-3.249125027
-0.6855722312
-0.3488236471
0.4398431
0.1030945564
0.5
0.005314
1
-10.20476633
-9.365390622
-1.4663628951
-0.3488236471
1.4815342
0.3639949151
0.5
0.066246
∑
-1.7441182353
0.0000000
Pct
N
E
Ө
A
143961.628
271411.057
355.7588497
B
149312.154
266950.471
Δ
5350.526
-4460.586
A
143961.628
271411.057
5.9092134
C
155043.181
272442.630
Δ
11081.553
1031.573
A
143961.628
271411.057
62.1153712
D
148138.017
277580.447
Δ
4176.389
6169.390
B
149312.154
266950.471
48.6452587
C
155043.181
272442.630
Δ
5731.027
5492.159
B
149312.154
266950.471
107.0034123
D
148138.017
277580.447
Δ
-1174.137
10629.976
C
155043.181
272442.630
159.2763886
D
148138.017
277580.447
Δ
-6905.164
5137.817
Tabel.Calculul orientariilor dupa compensare
Pct
N
E
Ө
A
143961.628
271411.057
41.9370488
1
147667.409
274279.691
Δ
3705.781
2868.634
A
143961.628
271411.057
395.1722826
2
150775.181
270893.368
Δ
6813.553
-517.689
B
149312.154
266950.471
114.0535180
1
147667.409
274279.691
Δ
-1644.745
7329.220
B
149312.154
266950.471
77.3804847
2
150775.181
270893.368
Δ
1463.027
3942.897
C
155043.181
272442.630
184.4600957
1
147667.409
274279.691
Δ
-7375.772
1837.061
C
155043.181
272442.630
222.1673739
2
150775.181
270893.368
Δ
-4268.000
-1549.262
D
148138.017
277580.447
290.9841037
1
147667.409
274279.691
Δ
-470.608
-3300.756
D
148138.017
277580.447
323.9140496
2
150775.181
270893.368
Δ
2637.164
-6687.079
1
147667.409
274279.691
347.2710257
2
150775.181
270893.368
Δ
3107.772
-3386.323
Tabel centralizator
Pct. Statie
Pct. Vizat
α*
Ө
z°
Necunoscunoscute
Pij
dN1
dE1
dN2
dE2
A
B
242.2352500
355.7588497
113.5235997
0.5
2
281.6486600
395.1723478
113.5236878
0.705823137
9.289801535
0.5
C
292.3854200
5.9092134
113.5237934
0.5
1
328.4131600
41.9369323
113.5237723
-8.3154377
10.74215495
0.5
D
348.5912200
62.1153712
113.5241512
0.5
∑
113.5238009
-8.3154377
10.74215495
0.705823137
9.289801535
B
C
128.6022700
48.6452587
320.0429887
0.5
2
157.3376400
77.3804380
320.0427980
-14.19199377
5.266005182
0.5
D
186.9609300
107.0034123
320.0424823
0.5
1
194.0108400
114.0534964
320.0426564
-8.269610832
-1.855774724
0.5
A
235.7166000
155.7588497
320.0422497
0.5
∑
320.0426350
-8.269610832
-1.855774724
-14.19199377
5.266005182
C
D
270.7654300
159.2763886
288.5109586
0.5
1
295.9492200
184.4601481
288.5109281
-2.024180033
-8.127082535
0.5
A
317.3982800
205.9092134
288.5109334
0.5
2
333.6565700
222.1673146
288.5107446
4.784092635
-13.17954381
0.5
B
360.1342100
248.6452587
288.5110487
0.5
∑
288.5109227
-2.024180033
-8.127082535
4.784092635
-13.17954381
D
A
206.4213400
262.1153712
55.6940312
0.5
1
235.2903300
290.9842052
55.6938752
18.90280533
-2.695052609
0.5
B
251.3099000
307.0034123
55.6935123
0.5
2
268.2202800
323.9141182
55.6938382
8.23880799
3.249125027
0.5
C
303.5827300
359.2763886
55.6936586
0.5
∑
55.6937831
18.90280533
-2.695052609
8.23880799
3.249125027
1
A
130.2983300
241.9369323
111.6386023
-8.3154377
10.74215495
0.5
B
202.4151300
314.0534964
111.6383664
-8.269610832
-1.855774724
0.5
2
235.6321700
347.2711723
111.6390023
-10.20476633
-9.365390622
10.20476633
9.365390622
0.5
C
272.8213400
-15.5398519
111.6388081
-2.024180033
-8.127082535
0.5
D
379.3454200
90.9842052
111.6387852
18.90280533
-2.695052609
0.5
∑
111.6387129
-9.911189559
-11.30114554
10.20476633
9.365390622
2
A
260.9769800
595.1723478
334.1953678
0.705823137
9.289801535
0.5
B
343.1851300
277.3804380
334.1953080
-14.19199377
5.266005182
0.5
C
87.9718500
22.1673146
334.1954646
4.784092635
-13.17954381
0.5
D
189.7186300
123.9141182
334.1954882
8.23880799
3.249125027
0.5
1
213.0755800
147.2711723
334.1955923
-10.20476633
-9.365390622
10.20476633
9.365390622
0.5
∑
334.1954442
-10.20476633
-9.365390622
9.741496321
9.365390622
Pct. Statie
Pct. Vizat
Pij
lij
vij
-dz
dӨ
Ө mas comp
Ө
A
B
0.5
-2.0116902
-2.1144190209
-0.1265040025
355.7588496835
355.758849683505
0.0000000
2
0.5
-1.1307552
-1.8850451979
-0.1265040025
-0.6515611819
395.1722826209
395.172282620861
0.0000000
C
0.5
-0.0746293
-0.1773580369
-0.1265040025
5.9092133896
5.909213389604
0.0000000
1
0.5
-0.2859600
0.7765162869
-0.1265040025
1.1652050413
41.9370487770
41.937048776964
0.0000000
D
0.5
3.5030347
3.4003059686
-0.1265040025
62.1153711560
62.115371156004
0.0000000
∑
0.0000000
0.0000000000
0.5136438595
B
C
0.5
3.5365772
3.4001553866
-0.1178482227
48.6452586947
48.645258694693
0.0000000
2
0.5
1.6298703
1.9597742799
-0.1178482227
0.4663257736
77.3804846566
77.380484656656
0.0000000
D
0.5
-1.5270010
-1.6634227603
-0.1178482227
107.0034123369
107.003412336878
0.0000000
1
0.5
0.2140882
0.2934495836
-0.1178482227
0.2157831363
114.0535180241
114.053518024081
0.0000000
A
0.5
-3.8535347
-3.9899564905
-0.1178482227
155.7588496835
155.758849683505
0.0000000
∑
0.0000000
0.0000000000
0.6821089099
C
D
0.5
0.3595115
0.3457477365
-0.0137637946
159.2763886367
159.276388636708
0.0000000
1
0.5
0.0545264
-0.4834707653
-0.0137637946
-0.5242333262
184.4600957149
184.460095714918
0.0000000
A
0.5
0.1070405
0.0932766911
-0.0137637946
205.9092133896
205.909213389604
0.0000000
2
0.5
-1.7811697
-1.2018812442
-0.0137637946
0.5930522994
222.1673738738
222.167373873689
0.0000000
B
0.5
1.2600914
1.2463275837
-0.0137637946
248.6452586947
248.645258694693
0.0000000
∑
0.0000000
0.0000000000
0.0688189732
D
A
0.5
2.4805460
2.8206508985
0.3401049226
262.1153711560
262.115371156004
0.0000000
1
0.5
0.9212261
0.2463786883
0.3401049226
-1.0149523817
290.9841037288
290.984103728611
0.0000000
B
0.5
-2.7076453
-2.3675403612
0.3401049226
307.0034123369
307.003412336878
0.0000000
2
0.5
0.5505201
0.2050528362
0.3401049226
-0.6855722312
323.9140495962
323.914049596261
0.0000000
C
0.5
-1.2446470
-0.9045420619
0.3401049226
359.2763886367
359.276388636708
0.0000000
∑
0.0000000
0.0000000000
-1.7005246129
1
A
0.5
-1.1062088
0.3839083124
0.3249120851
1.1652050413
241.9370487770
241.937048776964
0.0000000
B
0.5
-3.4643161
-2.9236209208
0.3249120851
0.2157831363
314.0535180241
314.053518024081
0.0000000
2
0.5
2.8944511
1.7530002912
0.3249120851
-1.4663628951
347.2710256862
347.271025686587
0.0000000
C
0.5
0.9526078
0.7532865328
0.3249120851
-0.5242333262
384.4600957149
384.460095714918
0.0000000
D
0.5
0.7234661
0.0334257844
0.3249120851
-1.0149523817
90.9841037288
90.984103728611
0.0000000
∑
0.0000000
0.0000000000
-1.6245604254
2
A
0.5
-0.7639210
-1.0666585487
0.3488236471
-0.6515611819
195.1722826209
195.172282620861
0.0000000
B
0.5
-1.3614510
-0.5463016014
0.3488236471
0.4663257736
277.3804846566
277.380484656656
0.0000000
C
0.5
0.2039947
1.1458706774
0.3488236471
0.5930522994
22.1673738738
22.167373873689
0.0000000
D
0.5
0.4398431
0.1030945564
0.3488236471
-0.6855722312
123.9140495962
123.914049596261
0.0000000
1
0.5
1.4815342
0.3639949151
0.3488236471
-1.4663628951
147.2710256862
147.271025686587
0.0000000
∑
0.0000000
0.0000000000
-1.7441182353
Estimarea preciziilor
a
[pvv]
43.73312515
So
2.186656257
b
Smi
3.092398935
c
s dN1=
0.152762932
sdE1=
0.246027566
s dN2=
0.198142839
s dE2=
0.201281026
d. s p1=
0.289596403
sp 2=
0.282444041
e. st=
0.047670037
f) Elipsa erorilor
1
2
q xx=
0.0024
q xx=
0.0041
q yy=
0.0063
0.0025
q yy=
0.0042
0.0027
q xy=
0.0013
-0.0039
q xy=
0.0014
-0.0001
ψ1
81.74337053
ψ2
51.51777231
λ1
0.006700066
λ1
0.005546026
λ2
0.002069847
λ2
0.002796044
a
0.178986411
a
0.162843886
b
0.099483179
b
0.1156252
TABEL CENTRALIZOATOR
Compensare
N1
E1
N2
E2
SN1
SE1
SN2
SE2
1(mas neponderate)
147667.4089
274279.6906
150775.181
270893.368
0.153
0.246
0.198
0.201
2(mas ponderate)
147667.4081
274279.6943
150775.18
270893.369
0.040
0.042
0.036
0.036
3(a=2 mm si b= 1,5mm/km)
147667.4095
274279.6957
150775.181
270893.37
0.042
0.044
0.037
0.038
4(a= 40mm si b=10mm/km)
147667.4081
274279.6943
150775.18
270893.369
0.042
0.044
0.037
0.038
5(met intersectiei multiple inainte)
147667.4101
274279.6873
0.052
0.075
6(met intersectiei multiple inapoi)
150775.177
270893.374
0.047
0.049