
|
|
|
In functie de elementele geometrice determinate si tinand cont de scara planului topografic exista patru metode principale de determinare: analitica, trigonometrica, grafica si mecanica.
La diversele lucrari de imbunatatiri funciare (irigatii, desecari, combaterea eroziunii solului etc.), calculul suprafetelor este util atat in scopul exploatarii cat si pentru determinarea debitelor de irigatie si evacuare.
Este metoda cea mai precisa de calcul a suprafetei aplicandu-se numai cu ajutorul coordonatelor rectangulare ale punctelor de pe conturul poligonului care delimiteaza suprafata in cauza.
La aceasta metoda exista doua posibilitati de calcul: cand se cunosc coordonatele echerice ale unui contur ce inchide suprafata de calculat si cand cunoastem coordonatele absolute ale punctelor de pe un contur oarecare.
In acest caz suprafata S in cauza (Fig. 62) se calculeaza ca o insumare de trapeze dupa calcularea prealabila a elementelor geometrice pentru acestea din coordonate.
Relatia de calcul este de forma:
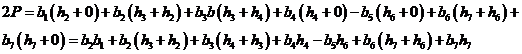
Obs. Atunci cand latura poligonului traverseaza axa A-B, suprafata triunghiului din exteriorul suprafetei (cel hasurat), va fi negativa in relatia de mai sus.
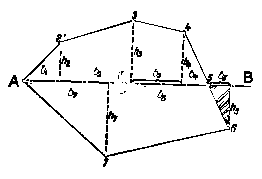
Fig.62.
Determinarea unei suprafete cu ajutorul coordonatelor echerice
In aceasta situatie exista doua relatii de calcul care se verifica una pe cealalta, iar pentru deductia lor vom lua un poligon oarecare avand punctele caracteristice 1-2-3-4 (Fig. 63), in care suprafata S in cauza (hasurata), se va obtine ca o insumare si scadere de trapeze dreptunghice rezultate din proiectarea poligonului pe axa de coordonate OY.
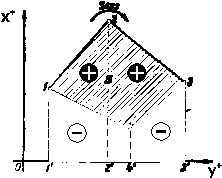
Fig.63. Deductia relatiilor de calcul a unei suprafete de teren prin metoda analitica
Urmarind figura de mai sus putem scrie urmatoarea relatie:
![]()
Dezvoltand produsele si reducand termenii asemenea vom obtine:
![]() si
si
![]()
unde: n - reprezinta nr. punctului;
n + 1 - reprezinta punct inainte;
n - 1 - reprezinta punct inapoi.
Suprafatele obtinute cu ambele relatii trebuie sa fie identice (m2).
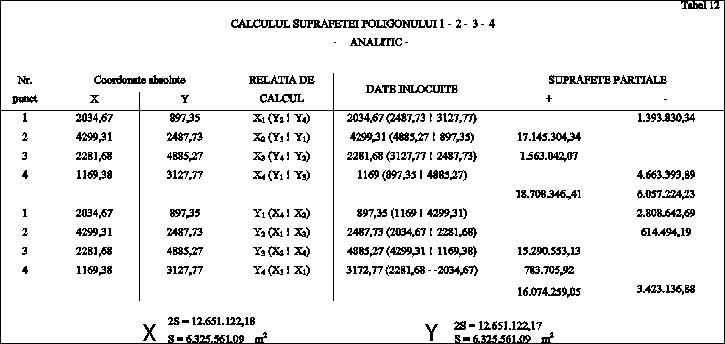
Vom lua in continuare un exemplu numeric de calcul referitor la poligonul din Fig. 100 in care toate calculele sunt redate in Tabelul 8.
Este o metoda numerica de calcul a suprafetelor de teren care se aplica in functie de instrumentele avute la dispozitie, cand ridicarea planimetrica se poate face numai prin distante sau prin distante si unghiuri.
Calculul suprafetelor de teren cand ridicarea planimetrica s-a facut prin distante
In acest caz un poligon oarecare 1-2-3-4-5 (Fig. 64) s-a descompus in cinci triunghiuri componente la care se vor masura pe teren toate laturile, iar relatia de calcul trigonometric pentru un triunghi este:
![]() - formula lui Heron
- formula lui Heron
in care: a, b, c - sunt laturile triunghiului
p - semiperimetru, ![]()
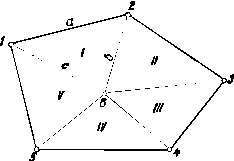
Fig. 64. Determinarea suprafetelor prin metoda
trigonometrica
in cazul unei ridicari planimetrice prin distante
Dupa calculul suprafetei fiecarui triunghi, acestea se vor insuma obtinand in final suprafata totala.
Tabelul 8. Calculul suprafetei poligonului 1-2-3-4. Analitic
Calculul suprafetei de teren cand ridicarea planimetrica s-a facut prin distante si unghiuri
De obicei aceasta metoda o aplicam cand ridicarea suprafetei de teren se face prin metoda radierii (Fig. 65), masurand pe teren laturile d1, d2, d3, d4 si d5 precum si unghiurile dintre ele u1, u2, u3, u4 si u5.
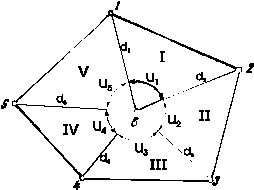
Fig. 65. Determinarea suprafetei prin metoda
trigonometrica
in cazul ridicarii planimetrice prin distante si unghiuri
In cele cinci triunghiuri care se formeaza (IV) se vor scrie pentru fiecare in parte relatia de calcul a suprafetei atunci cand se cunosc doua laturi si unghiul cuprins intre ele, astfel:
![]()
![]()
![]()
![]()
![]()
Prin insumarea ecuatiilor membru cu membru rezulta:
![]()
sau
![]()
unde: n - numarul de ordine al unghiurilor si laturilor pentru fiecare triunghi format