|
|
|
Este o metoda numerica de parcelare, care se va aplica suprafetelor de teren ridicate cu aparate de precizie, unde, redactarea planurilor s-a facut prin metoda coordonatelor rectangulare.
Intrucat suprafata de detasat S1 din suprafata poligonului A-C-D-E (Fig. 66) are forma unui trapez (A-M-N-E) in vederea stabilirii relatiilor de calcul vom adopta urmatoarele notatii pentru elementele acestuia: B - baza mare a trapezului, b - baza mica, h - inaltimea trapezului, l si K - laturile neparalele A-M si E-N; 1 si 2 - unghiuri adiacente bazei mari; u1 si u2 - proiectiile laturilor neparalele pe baza mare.
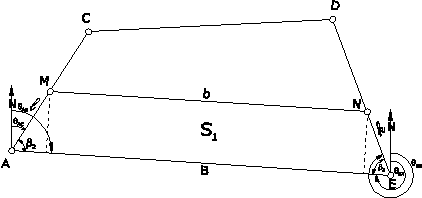
Fig. 66. Detasarea trigonometrica paralela
Baza mare a trapezului B (AE) se determina din coordonate:
Baza mica o deducem din relatiile pentru dubla determinare a inaltimii h
B - b = u1 + u2
, 
Din geometria plana
Din cele doua determinari ale inaltimii h, se poate scrie relatia de calcul pentru baza mica.
Dupa determinarea inaltimii cu una din cele doua relatii prezentate anterior, vom calcula lungimile l si K din triunghiurile dreptunghice rezultate prin proiectarea lor pe baza mare.
Cunoscand coordonatele polare ale punctelor M si N, vom calcula in continuare coordonatele absolute ale acestora cu relatiile:
si
( vezi Fig. 108)
Verificarea parcelarii - se va face printr-un calcul analitic a suprafetei trapezului A-M-N-E, iar rezultatul va trebui sa fie cel a suprafetei de detasat S1.
Transpunerea pe teren a suprafetei
detasate se va face prin masurarea pe aliniamentul AC si ED a
lungimilor l si K 
punctele M si N
care se borneaza.
Daca unghiurile adiacente bazei mari sunt optuze, vom calcula baza mare a trapezului B. Suma cotangentelor in acest caz este negativa iar relatia de calcul modificata va fi:
