BAZELE TEORIEI DECIZIEI

INCERTITUDINE DATORATA IGNORARII STARII NATURII

1. EXEMPLU INTRODUCTIV

In realitate exista o multitudine de cazuri in care problema decizionala prezinta mai multe stari posibile ale naturii, dar nu se cunoaste care este starea reala la un anumit moment de timp.

Exemplul pe care il vom detalia se refera la cazul in care avem doua stari ale naturii, pentru a putea analiza si compara toate strategiile posibile. Astfel, vom avea o observatie cu trei valori posibile si numai trei actiuni posibile, care vor genera 27 de strategii posibile.

Aflat in vizita in North Phiggins, domnul Nelson a fost informat ca in aceasta localitate pe timpul zilei poate fi numai vreme ploioasa sau numai vreme insorita. Daca ziua se dovedeste a fi ploioasa, atunci va incepe sa ploua la ora 11 dimineata si nu va inceta pana la 11 seara. In acest sens, a fost sfatuit ca in momentul in care paraseste camera la primele ore ale zilei, sa decida ce haine va purta tinand cont de indicatiile barometrului.

Barometrul poate indica urmatoarele situatii: vreme frumoasa, vreme incerta si vreme ploioasa. Domnul Nelson are la dispozitie trei randuri de haine: un rand de haine pentru vreme frumoasa, un rand de haine completat cu un impermeabil si un rand de haine completat cu un impermeabil, cizme, umbrela si palarie.

In ipoteza ca domnul Nelson nu stie cat de des ploua in North Phiggins, problema se refera la cazul in care avem doua stari ale naturii si trei actiuni posibile. Considerand ca scopul urmarit este de a nu fi surprins cu haine nepotrivite, domnul Nelson a construit urmatoarea matrice a pierderilor de utilitate:

Tabelul 1. Matricea pierderilor de utilitate

Actionand sub premiza rationalitatii, domnul Nelson se va baza pe indicatiile barometrului inainte de a decide ce rand de haine va purta in ziua respectiva. Vom considera indicatiile zilnice ale barometrului ca fiind o variabila aleatoare X care poate lua valori in urmatoarea multime:

In timp s-a observat faptul ca barometrul nu este ideal si s-au calculat probabilitatile de aparitie a fiecarei situatii indicate de acesta conditionate de starea reala a naturii:

Tabelul 2. Probabilitatile f( Xi | t ) = P( X = Xi | t )

Combinand datele din tabelele precedente vom obtine totalitatea strategiilor pe care le are la dispozitie domnul Nelson:

Tabelul 3. Lista strategiilor posibile

Analizand strategiile din acest tabel se observa ca unele sunt rationale si altele irationale. De exemplu, strategia s22 este in opozitie cu alegerea oricarei persoane rationale, iar strategiile s1, s14 si s27 ignora indicatiile barometrului si sunt alegeri ale unei persoane care nu se uita la barometru.

Domnul Nelson decide sa evalueze toate aceste strategii pe baza calcului pierderilor asteptate de utilitate L(t,s) corespunzatoare fiecarei stari ale naturii si fiecarei strategii. Rezultatele astfel obtinute sunt prezentate in tabelul urmator si se pot reprezenta grafic intr-un sistem de coordonate ( t1=L(t1,2) , t2=L(t2,s) ).

Tabelul 4. Pierderile asteptate de utilitate L(t,s)

Deoarece fiecare strategie prezinta doua pierderi asteptate de utilitate, vom putea reprezenta fiecare strategie ca un punct intr-un plan ale carui coordonate sunt pierderile asteptate de utilitate.

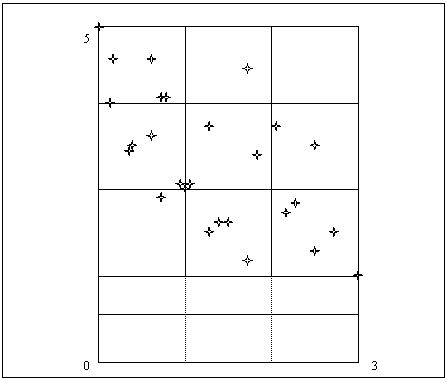
Figura 1. Strategii reprezentate in plan

O strategie dezirabila este aceea pentru care ambele perderi asteptate de utilitate sunt minime, adica acea strategie care este reprezentata printr-un punct situat cat mai la stanga si cat mai jos in plan. Se observa ca singurele care au aceasta proprietate sunt s1, s2, s5, s6, s9, s15 si s27.

Toate celelalte strategii sunt inadmisibile deoarece fiecare dintre aceste sunt dominate de cel putin una dintre strategiile mentionate.

Desi problema s-a redus considerabil prin eliminarea strategiilor dominate, ramanand numai opt strategii dezirabile, totusi nu stim care dintre acestea va fi cea preferata.

Sa presupunem ca domnul Nelson a selectat pana la urma doua strategii s6 si s15, dar nu s-a hotarat inca pe care sa o aleaga. Analizand situatia de pe graficul trasat anterior, domnul Nelson a trasat o dreapta imaginara intre cele doua strategii si a obtinut o multime infinita de strategii derivate sau mixte.

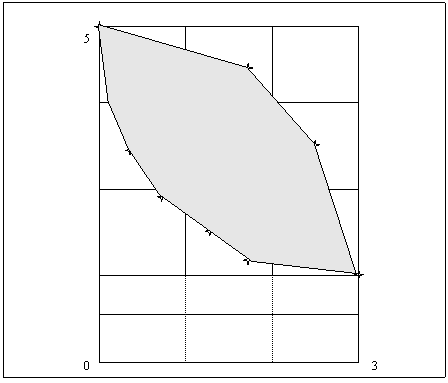
Figura 2. Multimea convexa a strategiilor

In urma acestui procedeu se observa ca o strategie considerata anterior a fi dominanta, si anume s9, devine dominata de o strategie derivata din combinatia a altor doua strategii dominante, si anume s6 si s15.

Continuand aceasta idee, vom trasa drepte intre toate strategiile initiale si vom obtine o multime convexa formata din puncte corespunzatoare tuturor strategiilor mixte. Aceasta multime defineste domeniul strategiilor posibile disponibile a fi alese de catre domnul Nelson, dar dupa cum am vazut anterior, foarte putine pot fi luate in considerare in cadrul unui algoritm de selectie.

Strategiile aflate pe frontiera inferioara a multimii convexe vor forma baza de plecare in cadrul procesului decizional de selectie a strategiei optime.

2. SEGMENTE DE DREAPTA SI MULTIMI CONVEXE

Se spune ca o strategie este pura daca asociaza o actiune fiecareia dintre observatiile posibile. Spre deosebire de aceasta, o strategie mixta sau derivata reprezinta o alegere a uneia dintre multimile de strategii pure, unde alegerea este facuta pe baza unui mecanism aleator.

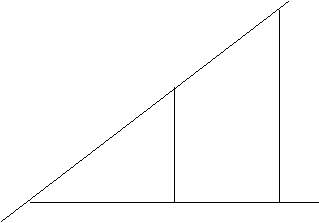In continuare vom discuta modul cum se construieste o strategie mixta. Vom considera o dreapta ce uneste doua puncte, (x0,y0) si (x1,y1), si un punct (x,y) situat la o distanta de (x0,y0) mai mare de 1,7 ori fata de distanta la care este situat (x1,y1) de (x0,y0).

Figura 3. Modul de construire a unei strategii mixte

Deoarece triunghiurile ABB' si ACC' sunt asemenea putem scrie raporturile

si obtinandu-se

x = x0 + 1,7 (x1 - x0) = -0,7 x0 + 1,7 x1

y = y0 + 1,7 (y1 - y0) = -0,7 y0 + 1,7 y1

Notand raportul 1,7 cu w vom avea urmatoarele relatii:

x = (1-w) x0 + w x1

y = (1-w) y0 + w y1

sau vectorial u = (1-w) u0 + w u1 , unde u, u0 si u1 reprezinta punctele (x,y) (x0,y0) si (x1,y1).

Tabelul 5. Pozitia punctului u la diferite valori ale lui w

Se observa ca pentru w subunitar si pozitiv, punctul u este o medie ponderata a celorlalte doua puncte, respectiv o strategie mixta.

O multime de puncte este un set de puncte care au proprietatea ca daca doua puncte apartin acestui set, atunci si segmentul de dreapta care uneste cele doua puncte apartine setului de puncte respectiv.

S

Punctul obtinut printr-o combinatie liniara a tuturor punctelor unei multimi convexe folosind ponderi egale, reprezinta centrul de greutate al acelei multimi.

Revenind la strategiile reprezentate in planul pierderilor asteptate de utilitate vom exprima:

L( t1,s ) = (1-w) L( t1,s0 ) + w L( t1,s1 )

L( t2,s ) = (1-w) L( t2,s0 ) + w L( t2,s1 )

unde s este o strategie mixta obtinuta prin combinarea strategiilor s0 si s1.

Considerand s0 si s1 ca fiind oricare din cele 27 de strategii pure, rezulta faptul ca multimea S care contine totalitatea strategiilor pure si mixte este o multime convexa.

Dupa cum am vazut in exemplul introductiv, domnul Nelson avea de ales una dintre cele 27 de strategii. Pentru a putea face acest lucru, el are nevoie de un criteriu de selectie care poate fi enuntat astfel: vom spune ca strategia s domina strategia s' daca sunt indeplinite conditiile urmatoare: a) L( t1,s )  L( t1,s' )

b)     L( t2,s )  L( t2,s' )

c)     strategiile nu sunt reprezentate prin acelasi punct in plan.

Aplicand acest criteriu asupra celor 27 de strategii pure si asupra strategiilor mixte grupate in multimea convexa S, vom alege un set de strategii admisibile. O strategie este admisibila daca nu este dominata de nici o alta strategie pura sau mixta. Clasa strategiilor admisibile corespunde unei portiuni a frontierei multimii convexe S.

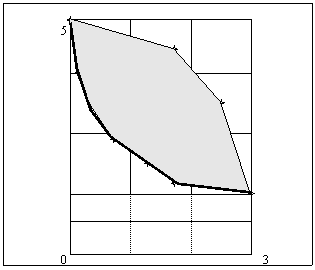
Figura 4. Frontiera strategiilor admisibile

3. STRATEGII BAYES SI DREPTE SUPORT

In general, o strategie Bayesiana corespunzatoare unor probabilitati apriori 1-w si w este o strategie care minimizeaza L(s ) = (1-w) L( t1,s ) + w L( t2,s ). O strategie Bayesiana poate fi localizata prin deplasarea unei linii paralele pana atinge multimea convexa S.

Pentru aceasta trebuie sa gasim forma coordonatelor unui punct care apartine unei drepte ce trece prin doua puncte ce reprezinta doua strategii in plan.

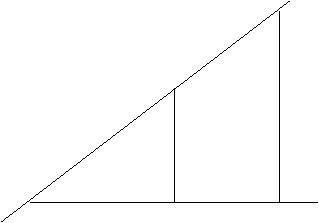
Figura 5. Modul de construire a unei strategii mixte

Deoarece triunghiurile ABB' si ACC' sunt asemenea putem scrie raporturile

si obtinandu-se

( x - x0 ) ( y1 - y0 ) = ( y - y0 ) ( x1 - x0 )

x ( y1 - y0 ) + y ( x0 - x1 ) = x0 y1 - y0 x1

a x + b y = c

Este adevarat faptul ca daca exista x si y astfel incat relatia sa fie adevarata, atunci punctul ale carui coordonate sunt x si y se afla pe linia dintre A si B. Mai precis, punctele de pe aceasta linie pot fi reprezentate de multimea . Se observa ca atat timp cat a si b sunt oricare doua numere nenule, atunci multimea de puncte ( x,y ) pentru care este adevarata relatia a x + b y = c reprezinta o dreapta.

In general, daca a si b nu sunt ambele nule, atunci a x + b y = c reprezinta o dreapta, iar a x + b y > c sunt puncte situate deasupra dreptei, in timp ce a x + b y < c sunt puncte situate sub linia respectiva. Daca coeficientii a, b si c sunt multiplicati cu un factor, atunci se obtine aceeasi dreapta ca in cazul initial.

Modificarea coeficientului c are ca efect deplasarea dreptei in sus daca c creste sau in jos daca c scade. Daca a = 0 atunci avem o dreapta orizontala, iar daca b = 0 avem o dreapta verticala.

Presupunand ca dreapta nu este verticala, putem face transformarile urmatoare:

a x + b y = c >>>b y = - a x + c>>>>>>y = m x + e

Coeficientul m se numeste panta dreptei, iar semnul acestuia este negativ daca a si b au acelasi semn, sau pozitiv daca a si b au semne contrare. Coeficientul e reprezinta inaltimea punctului de intersectie a axei verticala cu dreapta respectiva in cazul in care x este nul.

Efectul modificarii lui e este acelasi cu cel generat de modificarea lui c, in schimb modificarea lui m duce la rotirea dreptei.

Se spune ca o dreapta este dreapta suport a unei multimi S la punctul de frontiera u, daca u este punct pe frontiera lui S si dreapta trece prin u, iar multimea S nu este strapunsa de dreapta respectiva (S poate fi atinsa de dreapta).

Presupunem ca dreapta L = este dreapta suport pentru multimea S in punctul de frontiera u0. Fie s0 o strategie admisibila reprezentata de punctul u0. Atunci nici un punct al multimii convexe S nu se afla in zona T, respectiv la stanga si sub punctul u0. Deoarece u0 apartine lui S, acest punct nu apartine multimii T, dar este la frontiera acesteia, si vom putea duce o dreapta suport pentru ambele multimi prin respectivul punct.

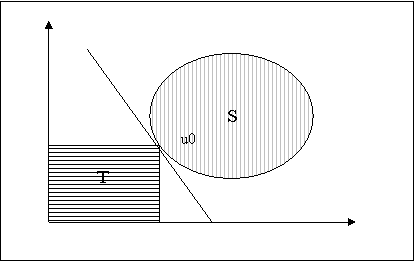
Figura 6. Dreapta suport

Analizand situatia de mai sus, se observa ca o dreapta suport poate fi trasata orizontal, vertical sau avand panta negativa, in functie de pozitiile celor doua multimi in plan. Se deduce astfel concluzia ca a si b au intotdeauna acelasi semn, deci a+b0.

Daca vom prelucra formula dreptei suport dedusa mai sus, prin impartirea cu a+b, vom avea

linia ( L1,L2 ) : a' L1 + b' L2 = c', cu proprietatea ca a' si b' sunt numere pozitive si subunitare. Astfel, putem nota a' cu 1-w si b' cu w, si pentru o strategie admisibila s reprezentata prin punctul u0, exista o pereche (1-w,w) astfel incat (1-w) L1 + w L2 = c' sa fie dreapta suport pentru multimea S in punctul u0, iar pentru toate celelalte puncte ale multimii S avem (1-w) L1 + w L2  c'.

In concluzie, fiecare strategie admisibila este o strategie Bayes pentru niste probabilitati apriori 1-w si w. Aceasta clasificare fundamentala a strategiilor admisibile deriva in principal din faptul ca doua multimi convexe care nu au nici un punct comun pot fi separate printr-o dreapta.

Similar, daca 1-w si w sunt doua probabilitati apriori, atunci strategiile Bayesiene corespunzatoare sunt admisibile.

Pentru a gasi o strategie Bayesiana vom trasa dreapta (1-w) L1 + w L2 = c sub multimea S, si vom mari parametrul c pana cand dreapta va atinge multimea S. Punctul in care drepta va intersecta multimea convexa S reprezinta o strategie Bayes corespunzatoare unor probabilitati apriori 1-w si w.

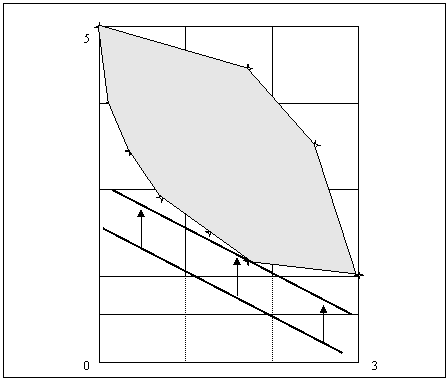
Figura 7. Determinarea unei strategii Bayes

Deoarece toate punctele multimii S sunt situate deasupra dreptei suport si pentru ca orice punct care domina un punct de pe dreapta suport se afla la stanga si sub acesta, rezulta faptul ca nici un punct al multimii S nu poate domina un punct al dreptei suport.

Aceasta inseamna ca nici o strategie nu poate domina una dintre strategiile Bayes, fiecare dintre strategiile Bayes, corespunzand unor probabilitati apriori, fiind admisibile.

In cazul in care w=0, dreapta suport va fi verticala si se va situa la stanga multimii S. Acest fapt se poate interpreta astfel: daca stim ca t2 este imposibila si t1 este starea naturii, atunci vom dori sa minimizam L(t1,s) indiferent de dimensiunea lui L(t2,2). In cazul in care w=1, dreapta suport va fi orizontala si se va situa sub multimea S, interpretarea fiind similara cazului anterior. Daca vom mari probabilitatea w, dreapta suport tinde sa devina orizontala, iar punctul corespunzator de pe frontiera se va deplasa in jos si spre dreapta. Aceste doua cazuri se numesc degenerate.

Pentru problema domnului Nelson se poate aplica teoria strategiilor Bayesiene in cazul in care decidentul cunoaste frecventa zilelor ploioase. Spre deosebire de aceasta problema, pot exista situatii in care starea naturii nu este aleatoare, deci nu are sens sa vorbim de probabilitatea sau frecventa cu care o stare poate aparea in mod sigur. O asemenea problema este aceea in care starea naturii t este viteza luminii. Aceasta stare poate fi un numar fixat care poate fi estimat printr-o serie de experimente care ne vor furniza o distributie de probabilitati, deci ar fi irational sa tratam viteza luminii ca un factor aleator.

Exista doua motive pentru care are sens sa lucram cu strategii Bayes: primul este acela ca acestea se pot obtine foarte usor, iar al doilea este ca in clasa strategiilor Bayesiene este cuprinsa si clasa strategiilor admisibile.

Faptul ca toate strategiile admisibile sunt strategii Bayes a fost demonstrat grafic. Totusi, putem trage si niste concluzii suplimentare. De exemplu, cel putin unul dintre punctele de intersectie ale dreptei suport cu multimea convexa nu este medie ponderata a altor puncte. Aceasta inseamna ca cel putin una dintre strategiile Bayesiene corespunzatoare unor probabilitati apriori (1-w,w) este o strategie pura. De fapt daca exista cateva strategii Bayesiene neechivalente corespunzatoare unor probabilitati apriori (1-w,w), acestea sunt construite pe baza strategiilor pure si a strategiilor derivate din acestea.

Strategiile s15, s18 si toate celelalte strategii derivate din acestea sunt strategii Bayes corespunzatoare probabilitatilor apriori 616 si 1016. Aceasta observatie ne duce la concluzia ca atat timp cat lucram cu strategiile Bayes corespunzatoare probabilitatilor apriori 1-w si w, nu va trebui sa ne facem griji in legatura cu strategiile derivate.

Deoarece exista probleme cu un numar finit de strategii pure, dar cu o infinitate de strategii derivate, este evident faptul ca din punct de vedere al volumului de calcul este indicata abordarea problemelor prin prisma strategiilor pure.

4. STRATEGII MINMAX

Revenind la problema domnului Nelson, un prieten il sfatuieste sa poarte imbracamintea pentru ploaie daca presupune ca vremea va fi ploioasa. In acest caz, pierderea de utilitate va fi 2. Dar domnul Nelson observa ca in cazul in care va fi zi insorita, pierderea de utilitate va fi 3. Analizand strategiile pure, alege s18 unde pierderea asteptata nu poate fi mai mare de 2.2, indiferent de starea naturii. In acest moment, prietenul sau ii atrage atentia ca oricare strategie va fi aplicata, starea naturii t care va apare va fi una care va maximiza pierderea de utilitate. Deci, va trebui aplicata acea strategie pentru care pierderea maxima va fi cat mai mica cu putinta.

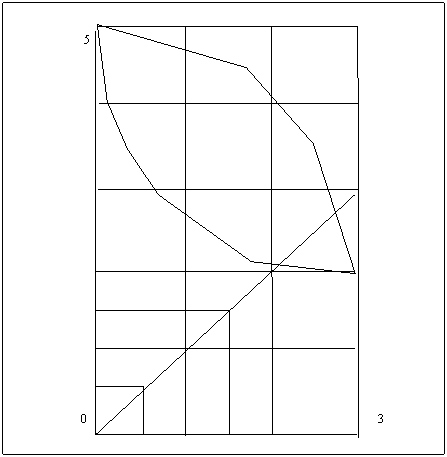
Figura 8. Strategii minmax

Multimea de puncte (L1,L2) pentru care cea mai mare dintre coordonate este unitatea, este multimea data de si este multimea de puncte de pe cele doua jumatati de drepte. Dreapta orizontala este cea pentru care L2=1 si L1<1, iar dreapta verticala este cea pentru care L1=1 si L2<1.

Combinand cele doua drepte cu cele doua axe vom obtine un patrat care are un colt in origine si unul in punctul (1,1). Considerand cazul general in care max( L1,L2 ) = c, vom obtine un patrat care are un colt in punctul (c,c). Pe masura ce vom mari numarul c, coltul din dreapta sus al patratului se va deplasa spre multimea S pana il va atinge.

Punctul in care patratul atinge pentru prima data multimea S este punctul corespunzator strategiei minmax. In problema noastra, acest punct este (30/14,30/14) care corespunde unei combinari dintre strategiile s18 si s27 cu probabilitatile 10/14 si 4/14.

Figura 9. Puncte minmax

5. RISC SAU REGRET

Matricea regretelor este derivata din matricea pierderilor de utilitate prin scaderea pierderii minime din fiecare element al matricii. Dupa cum se vede in figura 10, multimea S a fost deplasata vertical pana ce puntul (3,2) a devenit (3,2). In acest caz strategia minmax este in punctul (0.82,0.82) si este o mixtura intre s6 si s15 cu probabilitatile 0.8 si 0.2.

Tabelul 6. Matricea pierderilor de utilitate si matricea regretelor

Tabelul 7. Riscul sau regretele asteptate R(t,s)

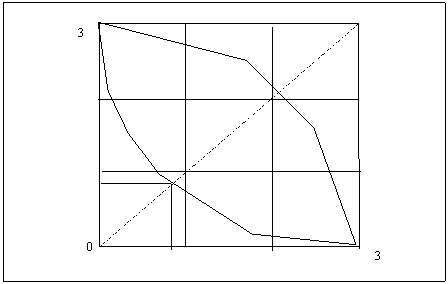
Figura 10. Strategia regretelor

6. DREPTE, PLANURI SI MULTIMI CONVEXE IN N DIMENSIUNI

In cazul problemei noastre am avut de reprezentat o pereche de numere printr-un punct in plan. Daca am fi avut de reprezentat un triplet (x,y,z) atunci acesta ar fi reprezentat un punct intr-un spatiu tridimensional. Datorita corespondentei dintre triplet si punctul din spatiu, teoremele din geometrie pot fi translatate in relatii algebrice.

Pentru o problema care implica patru sau mai multe stari ale naturii va trebui sa avem in vedere grupuri de patru sau mai multe numere. Si aici putem considera ca relatiile algebrice au corespondenta in geometrie, cu toate ca acestea sunt greu de vizualizat intr-un spatiu multidimensional.

In plan am prezentat urmatoarele relatii pentru o dreapta care trece prin doua puncte:

x = (1-w) x0 + w x1

y = (1-w) y0 + w y1

In spatiul tridimensional, un punct este reprezentat prin trei coordonate: u=(x,y,z).

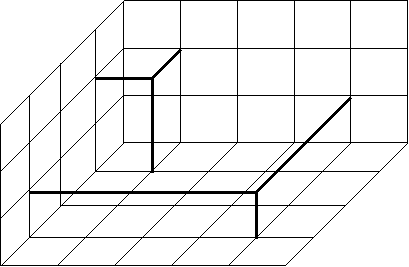
Figura 11. Reprezentarea unui punct in spatiul tridimensional

Dreapta care trece prin doua puncte dintr-un spatiu tridimensional este reprezentata de:

u : u = (1-w) u0 + w u1 , oricare w real

u0=(x0,y0,z0) u1=(x1,y1,z1)

x = (1-w) x0 + w x1

y = (1-w) y0 + w y1

z = (1-w) z0 + w z1

Pentru a obtine un segment de dreapta intre u0 si u1, trebuie pusa conditia ca 0w1.

Daca w1,w2,.,wm sunt m numere pozitive subunitare, atunci punctul u=w1u1+w2u2+.+wmum este media ponderata a punctelor u1,u2,.,um.

In spatiul tridimensional, un plan este reprezentat de o ecuatie liniara: unui plamn ii corespund patru numere a,b,c,d, care nu sunt toate nule, pentru care

In spatiul k dimensional, un hiperplan k-1 dimensional este dat de relatia:

P

unde b1,b2,.,bk nu sunt toate nule. In spatiul dimensional hiperplanul este o linie.

In spatiul tridimensional planul P este suport pentru multimea convexa S in punctul u daca u este un punct al lui P si daca S se afla in intregime de o parte a planului P. Acest lucru poate fi exprimat algebric astfel:

a x + b y + c z  d pentru toate punctele (x,y,z)  S

a x + b y + c z  d pentru toate punctele (x,y,z)  S

a x0 + b y0 + c z0 = d unde u0= (x0,y0,z0)  S

Daca S este o multime marginita si P un plan, atunci P poate fi deplasat paralel cu el insusi pana cand devine plan suport pentru multimea S. Daca S este o multime convexa si u este un punct de pe frontiera lui S, atunci exista un plan suport pentru S in punctul u. Daca unul dintre coeficientii a,b,c,d sunt egali cu zero, atunci planul P este paralel cu axa corespunzatoare.

Se spune ca un punct u este dominat de un punct v daca fiecare coordonata a lui u este cel putin la fel de mare fata de coordonata corespunzatoare a punctului v, si u este distinct de v. Partea admisibila a frontierei unei multimi convexe S consta in acele puncte de pe frontiera care nu sunt dominate de alte puncte ale lui S.

Dupa ce impartim coeficientii a,b,c si d cu numarul a+b+c vom obtine urmatoarele afirmatii:

daca u este pe partea admisibila a frontierei unei multimi convexe, atunci exista trei ponderi nenegative w1,w2 si w3 subunitare pentru care valoarea minima a mediei ponderate w1 x + w2 y + w3 z pentru (x,y,z) S este atinsa in punctul u.

daca w1,w2 si w3 sunt ponderi pozitive subunitare, orice punct u al lui S pentru care expresia w1 x + w2 y + w3 z este minimizata, se afla pe frontiera admisibila a lui S.

daca oricare dintre ponderi este egala cu zero, atunci in cel putin unul dintre punctele u care minimizeaza media ponderata este pe partea admisibila a frontierei multimii convexe S.

7. TREI SAU MAI MULTE STARI NECUNOSCUTE ALE NATURII

Vom presupune ca exista k stari posibile ale naturii. Corespunzatoare fiecarei strategii s vom avea k pierderi asteptate date de L(s) = ( L(t1,s), L(t2,s),., L(tk,s) ).

Daca s0 si s1 sunt doua strategii reprezentate de punctele L(s0) si L(s1), atunci prin combinarea strategiilor s0 si s1 cu probabilitatile 1-w si w vom obtine punctul (1-w) L(s0) + w L(s1). Aceasta inseamna ca toate punctele de pe segmentul de dreapta ce uneste L(s0) si L(s1) sunt corespunzatoare unor strategii mixte. De fapt, multimea punctelor de pierderi asteptate obtinuta folosind strategii derivate este multimea convexa generata de punctele reprezentand strategiile pure.

O strategie s este cel putin la fel de buna ca o strategie s0 daca L(ti,s)  L(ti,s0), i=1..k. O strategie s este echivalenta cu o strategie s0 daca L(ti,s) = L(ti,s0), i=1..k. O strategie s domina strategia s0 daca s este cel putin la fel de buna ca s0 si s nun este echivalenta cu s0. In acest caz fiecare coordonata a punctului ce reprezinta strategia s este cel mult egala cu coordonata corespunzatoare a punctului ce reprezinta strategia s0.

O strategie s este admisibila daca nu exista nici o strategie care sa o domine. La fel ca in sectiunile anterioare vom considera ca o multime convexa de pierderi asteptate este obtinuta prin luarea in considerare a tuturor strategiilor pure si mixte.

Strategia minmax este acea strategie pentru care cea mai mare dintre pierderile asteptate L(t1,s), L(t2,s).. L(tk,s) este cat mai mica cu putinta. Acest criteriu se numeste pierderi asteptate minmax. Geometric, o multime de puncte (x,y,z) pentru care max(x,y,z)=c consta in parte de trei plane paralele cu axele. Acestea sunt:

P1

P2

P1

Toate aceste trei plane au punctul (c,c,c) in comun.

Planele P1 si P2 au in comun segmentul de dreapta L12 = , planele P1 si P2 au in comun L13 = , iar planele P2si P3 au in comun L12

Strategia minmax se obtine deplasand multimea prin marirea lui c pana cand aceasta atinge multimea copnvexa S. Daca o atinge cu punctul (c,c,c) atunci strategia minmax s va avea proprietatea ca L(t1,s)  L(t2,s)  L(t2,s).

Figura 12. Diagrama

In general, pentru k stari ale naturii situatia se prezinta in felul urmator: strategia minmax este Bayes pentru niste probabilitati w1,w2,.,wk. Pierderile asteptate L(ti,s) corespunzatoare ponderilor nenule wi sunt egale intre ele.

Strategia minmax este obtinuta prin aplicarea criteriului minmax pentru riscuri sau regrete asteptate. Riscul este obtinut prin scaderea celei mai mici pierderi asteptate pentru ti din L(ti,s). Geometric, aceasta inseamna deplasarea lui S intr-o anumita directie.

O strategie Bayesiana se poate obtine nu numai prin minimizarea mediei ponderate a pierderilor asteptate, ci si prin minimizarea mediei ponderate a riscurilor.

L(s) = w1 L(t1,s) + w2 L(t2,s) + .. + wk L(tk,s)

R(s) = w1 R(t1,s) + w2 R(t2,s) + .. + wk R(tk,s)