
|
|
|
Vibratiile libere si neamortizate ale sistemelor cu doua grade de libertate
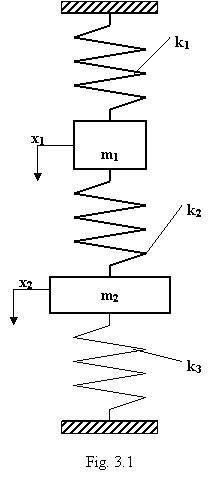 Sistemele cu doua grade de
libertate sunt constituite din doua mase concentrate, care sunt legate
prin intermediul unui resort de rigiditate k2, iar fiecare dintre
mase este legata in mod individual la un corp considerat rigid si
imobil prin cate un alt resort de rigiditate k1 si, respective,
k3. O reprezentatre schematica a sistemului cu doua grade
de libertate se poate vedea in figura 3.1. Este posibil ca intr-un system real
unul dintre resorturile acestea sa nu existe. Sistemul se considera
izolat.
Sistemele cu doua grade de
libertate sunt constituite din doua mase concentrate, care sunt legate
prin intermediul unui resort de rigiditate k2, iar fiecare dintre
mase este legata in mod individual la un corp considerat rigid si
imobil prin cate un alt resort de rigiditate k1 si, respective,
k3. O reprezentatre schematica a sistemului cu doua grade
de libertate se poate vedea in figura 3.1. Este posibil ca intr-un system real
unul dintre resorturile acestea sa nu existe. Sistemul se considera
izolat.
Un exemplu de astfel de sistem este autovehiculul sprijinit elastic de sasiu, sasiul fiind la randul lui sprijinit elastic pe sol cu ajutorul sistemului format de cele patru roti.
In starea initiala, ansamblul din figura 3.1 este in echilibru, datorita compensarii actiunii fortelor de greutate de catre fortele elastice din resorturi. Scoaterea sistemului din aceasta stare de echilibru este posibila prin deplasarea unuia sau a ambelor corpuri si/sau prin imprimarea unei viteze unuia sau ambelor corpuri, la momentul initial.
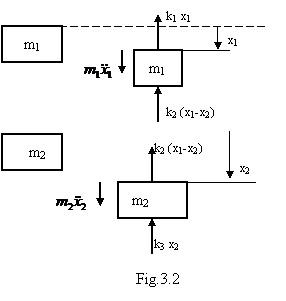
Sistemul se afla in stare de oscilatie ca urmare a prezentei unei perturbatii initiale de tipul celor mentionate anterior. Corpurile au fost isolate prin ruperea legaturilor dintre ele si a celor dintre corpuri si sistemul exterior imobil. Figura 3.2 prezinta corpurile izolate asupra carora actioneaza fortele de legatura si forta proportionala cu acceleratia fiecaruia dintre cele doua corpuri. Presupunand ca in timpul miscarii oscilatorii a sistemului, deplasarea corpului 2 este mai mica decat cea a corpului 1, se pot scrie ecuatiile de echilibru dinamic, in conformitate cu principiul doi al mecanicii, relativ la copurile reprezentate in figura 3.2.
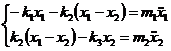 (1)
(1)
Acest sistem de ecuatii diferentiale cu coeficienti constanti este de tip omogen, datorita absentei unor termeni dependenti explicit de parametrul timp. Acest lucru se poate constata din forma echivalenta a ecuatiilor:
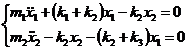 (2)
(2)
Cele doua ecuatii
diferentiale depind fiecare dintre ele de valorile instantanee ale
elongatiilor si acceleratiile fiecaruia dintre corpuri.
Altfel spus, prima ecuatie, care descrie comportarea corpului de masa
m1, contine produsul k2x2,
care se refera la deplasarea in timp a masei m2, iar a doua
ecuatie care descrie comportarea corpului de masa m2,
contine produsul (k2 + k3)x1,
care se refera la deplasarea in timp a masei m1. Un astfel de sistem de ecuatii nu se
poate rezolva prin solutionarea individuala a fiecareia dintre
ecuatii. El poarta denumirea de sistem cuplat, termenii de cuplare
fiind produsele ![]() si, respectiv,
si, respectiv, ![]() .
.
O formulare matriciala a sistemului (..) este de forma:
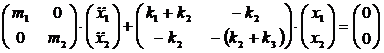 , (3)
, (3)
sau, intr-o forma mai concisa,
![]()
Unde 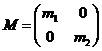 este denumita matricea de inertie, iar
este denumita matricea de inertie, iar 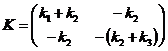 este matricea de rigiditate.
este matricea de rigiditate.
Se considera ca, sub
actiunea perturbatiilor suferite la momentul initial, sistemul
executa oscilatii armonice, adica elongatiile instantanee
ale fiecarui corp, ![]() si
si ![]() , se pot modela ca functii sinus de acceasi
pulsatie.
, se pot modela ca functii sinus de acceasi
pulsatie.
![]() (4)
(4)
Ca solutii ale sistemului (),
functiile () vor verifica ecuatiile sistemului de ecuatii
diferentiale. Inlocuind in ecuatii expresiile armonice ale
deplasarilor instantanee si ale acceleratiilor, dupa
impartirea fiecarei ecuatii la termenul nenul ![]() , se vor obtine:
, se vor obtine:
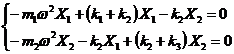 , (5)
, (5)
echivalente cu:
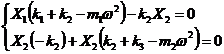 (6)
(6)
Din punct de vedere matematic,
sistemul () este liniar, in raport cu necunoscutele ![]() ,
,![]() . Termenii liberi nuli fac ca sistemul sa fie omogen.
Prin urmare, daca detreminantul format cu coeficientii
necunoscutelor, numit determinant principal, este diferit de zero, sistemul
admite numai solutii nule, adica
. Termenii liberi nuli fac ca sistemul sa fie omogen.
Prin urmare, daca detreminantul format cu coeficientii
necunoscutelor, numit determinant principal, este diferit de zero, sistemul
admite numai solutii nule, adica ![]() si
si ![]() . In situatia mentionata, din punct de vedere
fizic se poate spune ca sistemul este in echilibru, negasindu-se in
stare de oscilatie. Solutia nula nu prezinta interes
tehnic.
. In situatia mentionata, din punct de vedere
fizic se poate spune ca sistemul este in echilibru, negasindu-se in
stare de oscilatie. Solutia nula nu prezinta interes
tehnic.
Daca determinantul principal, a carui forma explicita este
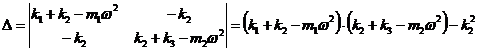 , (7)
, (7)
are
valoarea zero, ![]() , atunci sistemul algebric liniar si omogen admite o
infinitate de solutii. Conditia
, atunci sistemul algebric liniar si omogen admite o
infinitate de solutii. Conditia ![]() poate fi privita
ca o ecuatie cu necunoscuta ω, de forma:
poate fi privita
ca o ecuatie cu necunoscuta ω, de forma:
![]() (8)
(8)
Aceasta ecuatie algebrica a pulsatiilor este de tip bipatrat si are discriminantul egal cu:
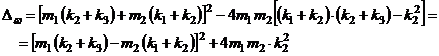 (9)
(9)
Ca suma de patrate ale
unor numere reale, nenule, discriminantul ![]() este intotdeauna un
numar strict pozitiv,
este intotdeauna un
numar strict pozitiv, ![]() Solutiile ale ecuatiei
bipatrate sunt distincte:
Solutiile ale ecuatiei
bipatrate sunt distincte:
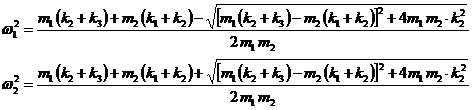 (10)
(10)
Se observa ca ![]() si
si ![]() sunt numere pozitive.
Rezulta ca solutiile numere reale ale ecuatiei
bipatrate sunt in numar de doua. Ele se numesc pulsatii proprii.
Astfel pulsatiile proprii ale sistemului sunt marimile exprimate
prin:
sunt numere pozitive.
Rezulta ca solutiile numere reale ale ecuatiei
bipatrate sunt in numar de doua. Ele se numesc pulsatii proprii.
Astfel pulsatiile proprii ale sistemului sunt marimile exprimate
prin:
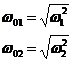 (11)
(11)
Raspunsul sistemului cu
doua grade de libertate va depinde de pozitionarea pulsatiei
fortelor excitatoare relativ la pulsatiile proprii ale structurii. In
absenta amortizarii, amplitudinea oscilatiilor creste,
teoretic, pana la o valoare infinita. Practic, nici un sistem tehnic
nu este lipsit de amortizarea inerenta introdusa de fortele de
frecare ce apar fie la deplasarea relativa a doua piese, fie in
interiorul materialului elementului elastic, care se deformeaza alternativ
in prezenta vibratiilor.
Vibratiile fortate
neamortizate ale sistemelor cu doua grade de libertate
 Sisteme
tehnice cuprind cel mai adesea mecanisme antrenate de elemente de
actionare, care imprima elementelor constitutive ale mecanismului
miscari de rotatie sau de translatie cu o
frecventa egala cu cea a elementului de actionare.
Mecanismul insusi poate fi privit, insa, ca un ansamblu de mase
inertiale legate prin elemente caracterizate de o elastricitate proprie
(sau o rigiditate) proprie. Daca evaluarea acestor rigiditati
evidentiaza una de valoare mai redusa, cu un ordin de marime sau
mai mult, elementul respectiv poate fi privit ca o legatura
elastica intre doua mase inertiale. Dintre acestea, cel
putin una este legata elastic la un sasiu fix. In cazul cel mai
general, ambele structuri de tip masa concentrata se vor considera
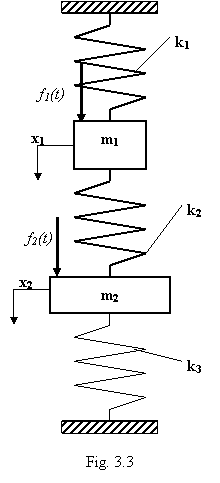
legate la sasiu, conform figurii 3.3. Conform acestei reprezentari,
fiecare corp este actionat cu o forta excitatoare. Pentru
simplificare, se va studia mai intai cazul in care cele doua forte de
tip armonic au aceeasi pulsatie ω,
Sisteme
tehnice cuprind cel mai adesea mecanisme antrenate de elemente de
actionare, care imprima elementelor constitutive ale mecanismului
miscari de rotatie sau de translatie cu o
frecventa egala cu cea a elementului de actionare.
Mecanismul insusi poate fi privit, insa, ca un ansamblu de mase
inertiale legate prin elemente caracterizate de o elastricitate proprie
(sau o rigiditate) proprie. Daca evaluarea acestor rigiditati
evidentiaza una de valoare mai redusa, cu un ordin de marime sau
mai mult, elementul respectiv poate fi privit ca o legatura
elastica intre doua mase inertiale. Dintre acestea, cel
putin una este legata elastic la un sasiu fix. In cazul cel mai
general, ambele structuri de tip masa concentrata se vor considera
legate la sasiu, conform figurii 3.3. Conform acestei reprezentari,
fiecare corp este actionat cu o forta excitatoare. Pentru
simplificare, se va studia mai intai cazul in care cele doua forte de
tip armonic au aceeasi pulsatie ω,
![]()
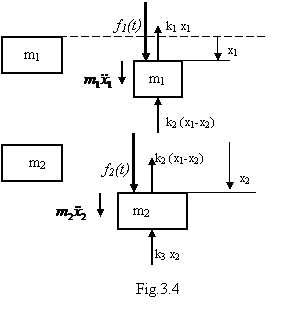
Aplicand metoda izolarii corpurilor, pentru fiecare dintre ele se marcheaza fortele elastice din legaturi, forta excitatoare, rezultanta acestora fiind egala cu produsul dintre masa corpului si acceleratia imprimata lui, ca in figura 3.4.
Ecuatiile de echilibru dinamic pentru sistemul corpurilor va fi:
![]()
Sistemul de doua ecuatii
diferentiale are drept necunoscute deplasarile instantanee ![]() si
si ![]() ale corpurilor. Fortele
excitatoare vor fi termeni liberi intr-un astfel de model matematic:
ale corpurilor. Fortele
excitatoare vor fi termeni liberi intr-un astfel de model matematic:
![]()
 Excitatiile
au pulsatia comuna ω, astfel ca este de asteptat ca
structura elastica sa oscileze armonic cu aceasta pulsatie.
De aceea deplasarile instantanee se vor cauta de forma:
Excitatiile
au pulsatia comuna ω, astfel ca este de asteptat ca
structura elastica sa oscileze armonic cu aceasta pulsatie.
De aceea deplasarile instantanee se vor cauta de forma:
![]() ,
,
ceea ce transforma problema initiala intr-una de determinare a amplitudinilor independente de timp ale deplasarilor armonice.
Ca solutii ale sistemului (),
functiile () vor verifica ecuatiile sistemului de ecuatii
diferentiale. Inlocuind in ecuatii expresiile armonice ale
deplasarilor instantanee si ale acceleratiilor, dupa impartirea
fiecarei ecuatii la termenul nenul ![]() , se vor obtine:
, se vor obtine:
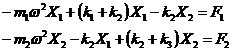 ,
,
echivalente cu:
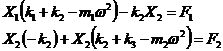
Sub aceasta forma, sistemul s-a transformat intr-un sistem liniar, avand drept necunoscute amplitudinile constante in timp, X1 si X2. Determinantul principal, ai carui termeni sunt coeficientii necunoscutelor, este:
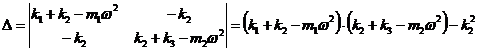
In cazul in care determinantul
principal este nul, adica ![]() , sistemul oscileaza cu amplitudine, teoretic,
infinita. Acest lucru indica faptul ca se manifesta
fenomenul de rezonanta pentru acele valori ale pulsatiilor
ω, pentru care este indeplinita conditia
, sistemul oscileaza cu amplitudine, teoretic,
infinita. Acest lucru indica faptul ca se manifesta
fenomenul de rezonanta pentru acele valori ale pulsatiilor
ω, pentru care este indeplinita conditia ![]() . Aceasta conditie este, din punct de vedere
matematic, o ecuatie cu necunoscuta ω:
. Aceasta conditie este, din punct de vedere
matematic, o ecuatie cu necunoscuta ω:
![]()
Ecuatia algebrica a pulsatiilor este de tip bipatrat si are discriminantul egal cu:
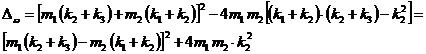
Ca suma de patrate ale
unor numere reale, nenule, discriminantul ![]() este intotdeauna un
numar strict pozitiv,
este intotdeauna un
numar strict pozitiv, ![]() Solutiile ale
ecuatiei bipatrate sunt distincte:
Solutiile ale
ecuatiei bipatrate sunt distincte:
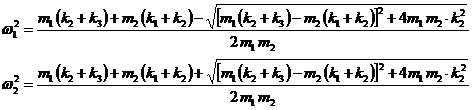
Se observa ca ![]() si
si ![]() sunt numere pozitive. Rezulta
ca solutiile numere reale ale ecuatiei bipatrate sunt in
numar de doua. Ele se numesc pulsatii proprii. Astfel pulsatiile
proprii ale sistemului sunt marimile exprimate prin:
sunt numere pozitive. Rezulta
ca solutiile numere reale ale ecuatiei bipatrate sunt in
numar de doua. Ele se numesc pulsatii proprii. Astfel pulsatiile
proprii ale sistemului sunt marimile exprimate prin:
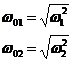
Atunci cand fortele excitatoare,
![]()
au pulsatii ω apropiate valoric de pulsatiile proprii determinate cu relatiile () si (), sistemul, chiar daca nu lucreaza in regim pur de rezonanta, are amplitudini mari de oscilatie, care genereaza tensiuni mecanice excesive in materialul elementelor elastice de legatura. Aceste tensiuni sunt variabile, de tip alternant simetric, daca excitatia este armonica. Materialul elementului solicitat in regim variabil va prezenta relativ rapid fenomenul de oboseala, caracterizat prin diminuarea severa a rezistentei mecanice. Drept urmare, are loc o deteriorare accelerata a pieselor supuse regimului mentionat. O functionare in conditiile descrise mai sus este de evitat, de aceea orice sistem mecanic se evaluaeza sub aspectul determinarii pulsatiilor proprii inca din faza de proiectare.
In situatia favorabila in
care sistemul este solicitat de forte excitatoare avand pulsatia
diferita valoric de una dintre pulsatiile proprii, se pot determina
expresiile amplitudinilor de oscilatie ale corpurilor de mase m1
si m2. ca solutii ale sistemului algebric liniar, de tip
Cramer (Δ![]() ). Se calculeaza determinantii:
). Se calculeaza determinantii:
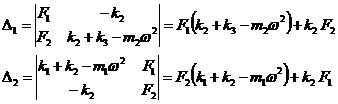
Cu acestea, amplitudinile oscilatiilor armonice ale maselor m1 si m2 sunt:
![]()
![]()
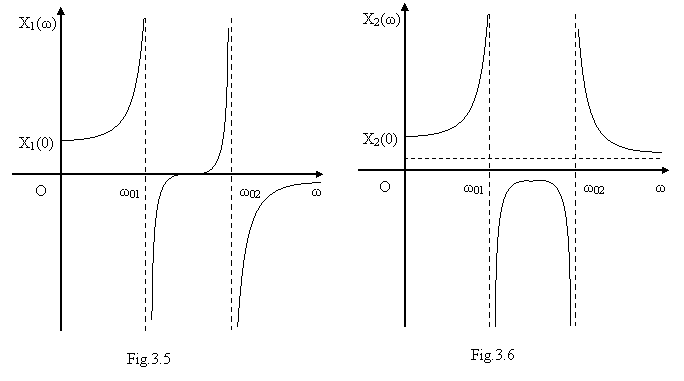
Amplitudinile oscilatiilor nu
depind de timp, dar sunt functii de pulsatia fortei excitatoare
ω. Reprezentarea grafica a variatiei amplitudinilor in raport de
ω se poate vedea in figurile 3.5 si 3.6. Ca urmare a faptului ca
numitorul are intotdeauna exact doua radacini reale si
distincte, indiferent de valorile pozitive ale celorlalti parametri,
graficele functiilor ![]() si
si ![]() au intotdeauna
doua asimptote verticale, care corespund valorilor absciselor egale cu
pulsatiile proprii
au intotdeauna
doua asimptote verticale, care corespund valorilor absciselor egale cu
pulsatiile proprii ![]() si
si ![]() ale sistemului
oscilant.
ale sistemului
oscilant.
Absorbitorul dinamic neamortizat
Absorbitorul dinamic este o masa inertiala auxiliara, atasata unei mase inertiale utile cu scopul de a-i elimina comportamentul vibratoriu la o anumita frecventa, care coincide cu frecventa de lucru a masei utile. Absorbitorul este o solutie a problemei ingineresti concrete care se poate formula astfel: "Cum se opreste din oscilatie un corp legat elastic de suportul lui rigid, la o anumita frecventa?" Figura 3.5 prezinta schema de principiu a absorbitorului dinamic constituit din masa utila m2 si masa suplimentara m1. Dupa cum se poate constata, acesta este un caz particular de sistem ce executa oscilatii fortate neamortizate, la care lipseste resortul ce leaga masa m1 de suportul imobil (k1=0), iar excitatia exterioara se aplica numai masei utile m2 (f1(t) =0). Sistemul de ecuatii () conduce la sistemul algebric (), in conditiile particulare mentionate.
Determinantul principal al sistemului algebric va fi:
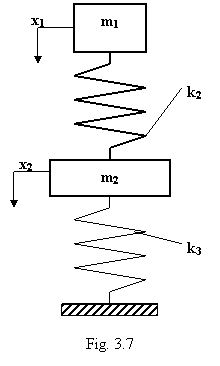
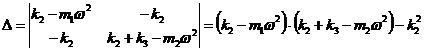 ,
,
iar
amplitudinea de oscilatie a masei utile, ![]() se exprima prin
relatia:
se exprima prin
relatia:
![]() .
.
Daca alegem masa aditionala m1 si arcul k2 astfel incat sa fie indeplinita conditia:
![]() ,
,
ceea ce este echivalent cu o corelare intre pulsatia excitatoare ω si structura atasata suplimentar:
![]() ,
,
Din relatia (), se
observa faptul ca numaratorul fractiei prin care se
exprima amplitudinea de oscilatie a masei utile devine nul. Prin
urmare, nula este amplitudinea de oscilatie a corpului m2,
adica![]() . Masa m2 inceteaza sa mai oscileze la
acea pulsatie a fortei excitatoare care indeplineste
conditia (). Daca, in plus, impunem ca pulsatia excitatoare
ω sa coincida cu pulsatia proprie a sistemului format din
masa utila m2 si arcul de rigiditate k3,
adica:
. Masa m2 inceteaza sa mai oscileze la
acea pulsatie a fortei excitatoare care indeplineste
conditia (). Daca, in plus, impunem ca pulsatia excitatoare
ω sa coincida cu pulsatia proprie a sistemului format din
masa utila m2 si arcul de rigiditate k3,
adica:
![]() ,
,
atunci corpul 2 inceteaza sa oscileze la pulsatia la care, in absenta absorbitorului m1, s-ar gasi in regim de rezonanta.
Sistemul format din masa suplimentara m1 si masa principala m1 are doua grade de libertate, fiind caracterizat de doua pulsatii proprii, determinate cu relatiile () si ().
Recapituland, putem spune ca masa m2 se comporta diferit in absenta sau in prezenta absorbitorului:
1. Cand masa m2 este
legata prin intermediul arcului de rigiditate k3 la suportul
fix, ea are o amplitudine infinita de oscilatie atunci cand
pulsatia fortei excitatoare coincide cu pulsatia proprie: 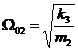 .
.
2. Cand masa m2 este
legata prin intermediul arcului de rigiditate k3 la suportul
fix si prin intermediul arcului de rigiditate k2 la masa m1,
ea nu oscileaza atunci cand
pulsatia fortei excitatoare coincide cu pulsatia proprie,
daca este indeplinita conditia: ![]()
Este de observat faptul ca atasarea masei auxiliare m1 face ca sistemul aflat in vibratie sa aiba doua grade de libertate si, implicit, doua pulsatii proprii, diferite de cea a sistemului masa m2 - resort k3.
Graficul variatiei
amplitudinii ![]() in functie de
pulsatia fortei excitatoare de tip armonic
in functie de
pulsatia fortei excitatoare de tip armonic ![]() a fost trasat in
figura 3.6. Curbelea reprezentate cu linie intrerupta caracterizeaza
evolutia amplitudinii unui sistem vibratoriu cu o singura
pulsatie proprie (cazul 1.), iar curbele trasate cu linie continua,
separate de doua asimptote verticale cauate de doua pulsatii
proprii, constituie comportarea sistemului masa-absorbitor (cazul 2.).
a fost trasat in
figura 3.6. Curbelea reprezentate cu linie intrerupta caracterizeaza
evolutia amplitudinii unui sistem vibratoriu cu o singura
pulsatie proprie (cazul 1.), iar curbele trasate cu linie continua,
separate de doua asimptote verticale cauate de doua pulsatii
proprii, constituie comportarea sistemului masa-absorbitor (cazul 2.).
Fig.3.6
Egalarea rapoartelor ![]() poarta numele de relatia de acordare a
absorbitorului dinamic.
poarta numele de relatia de acordare a
absorbitorului dinamic.
Daca un absorbitor este
acordat corect, adica patratul pulsatiei proprii al cuplului
masa utila m2 si resort k3, ![]() , iar raportul adimensional al maselor utila si
auxiliara este notat
, iar raportul adimensional al maselor utila si
auxiliara este notat ![]() , ecuatia pulsatiilor proprii ia o noua
forma. Din relatiile mentionate anterior se pot scrie
urmatoarele expresii:
, ecuatia pulsatiilor proprii ia o noua
forma. Din relatiile mentionate anterior se pot scrie
urmatoarele expresii:
![]()
![]()
Cu acestea, ecuatia ![]() devine:
devine:
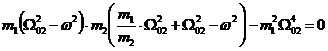
Cu notatia ![]() , ecuatia se rescrie astfel:
, ecuatia se rescrie astfel:
![]()
Reformularea ecuatiei consta in desfacerea parantezelor prin efectuarea inmultirilor si ordonarea termenilor in sensul scrierii puterilor necunoscutei ω in ordine descrescatoare. Se obtine ecuatia bipatrata a pulsatiilor:
![]()
Rezultatele unei ecuatii sunt
mai usor de interpretat din punct de vedere tehnic atunci cand necunoscuta
este o marime adimensionala. In acest caz, raportul dintre
pulsatia fortei excitatoare si pulsatia proprie a masei
utile in absenta absorbitorului, ![]() , constituie necunoscuta adimensionala a ecuatiei:
, constituie necunoscuta adimensionala a ecuatiei:
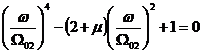
Ecuatia bipatrata a
pulsatiilor adimensionale are discriminantul dependent de raportul
adimensional al maselor, ![]() . El este:
. El este:
![]()
Cu acestea se poate da expresia solutiei ecuatiei pulsatiilor adimensionale:
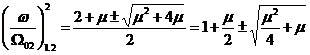
Dintre cele patru solutii ale ecuatiei, semnificatie fizica au numai cele pozitive:
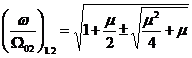
Cu aceste solutii adimensionale se pot da expresiile pulsatiilor proprii ale sistemului cu doua grade de libertate al absorbitorului dinamic:
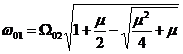
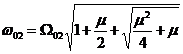
Formularea adimensionala a solutiilor nu este doar un artificiu matematic, ci este un instrument de interpretare din punct de vedere tehnic, practic, al unui rezultat matematic. In continuare vom discuta solutiile date mai sus.
Daca raportul adimensional al
maselor,![]() , este apropiat de zero, adica masa suplimentara
este foarte mica in comparatie cu masa a carei oscialtie
trebuie controlata, se constata ca cele doua pulsatii
proprii sunt foarte apropiate valoric de pulsatia proprie a masei
principale legate elastic de suportul fix. Cu alte cuvinte, absorbitorul este
ineficient pentru ca exista riscul major de intrare in regimul de
lucru de tip rezonanta la cea mai mica abatere a unui parametru,
din cauza unor tolerante tehnologice sau datorita unei minore
modificari a pulsatiei fortei excitatoare.
, este apropiat de zero, adica masa suplimentara
este foarte mica in comparatie cu masa a carei oscialtie
trebuie controlata, se constata ca cele doua pulsatii
proprii sunt foarte apropiate valoric de pulsatia proprie a masei
principale legate elastic de suportul fix. Cu alte cuvinte, absorbitorul este
ineficient pentru ca exista riscul major de intrare in regimul de
lucru de tip rezonanta la cea mai mica abatere a unui parametru,
din cauza unor tolerante tehnologice sau datorita unei minore
modificari a pulsatiei fortei excitatoare.
Pentru a separa pulsatiile
proprii ale sistemului cu absorbitor dinamic, este necesara cresterea
valorii raportului ![]() . Figura 3.8 a fost trasata pentru a arata
distantarea pulsatiilor adimensionale odata cu marirea
raportului μ.
. Figura 3.8 a fost trasata pentru a arata
distantarea pulsatiilor adimensionale odata cu marirea
raportului μ.
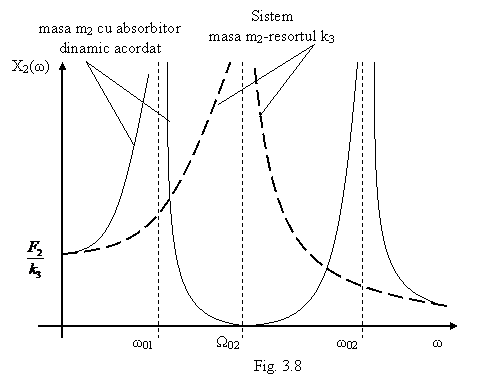
Se contureaza o intrebare fireasca: "Cat de
mare trebuie sa fie masa aditionala, pentru a avea un absorbitor
optim?" Criteriile de optim pot fi diverse. Dintre ele se pot evidentia
doua foarte importante.
Unul dintre ele se refera la gabaritul dispozitivului care are nevoie de un absorbitor dinamic. Orice masa suplimentara asociata unui resort aduce cu sine o marire a gabaritului. Prin urmare, optim ar fi un sistem la care masa suplimentara este redusa ca volum (masa redusa), iar elementul elastic sa fie conceput astfel ca, la o rigiditate impusa de conditia de acordare, gabaritul lui sa fie minim. Daca se utilizeaza arcuri elicoidale de intindere-compresiune, o rigiditate mare asociata cu un gabarit redus se poate obtine atunci cand se folosesc arcuri legate in paralel, montate coaxial, introduse unul in celalalt.
Un al doilea criteriu de optim se
refera la separarea neta dintre noile pulsatii proprii,
aparute ca urmare a introducerii masei suplimentare a absorbitorului
dinamic, si pulsatia la care sistemul lucreaza efectiv, care
este pulsatia ω a excitatorului. Aceasta se traduce printr-o diferenta
![]() de valoare mare.
Reprezentarea functiei
de valoare mare.
Reprezentarea functiei 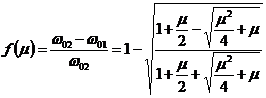 (fig.3.8) arata
ca o separare neta a pulsatiilor proprii incepe de la raportul
maselor μ = ..
(fig.3.8) arata
ca o separare neta a pulsatiilor proprii incepe de la raportul
maselor μ = ..
Fig 3.8
Este foarte important sa se
tina seama de separarea neta a pulsatiilor proprii mai ales
in cazul sistemelor in care pulsatia excitatoare variaza in jurul
valorii date de relatia 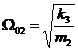 .
.
In proiectarea absorbitorului
dinamic se poate pleca de la o valoare aleasa a raportului ![]() , care va permite calculul direct al raportului μ al maselor, astfel ca μ < 1. Cunoscand μ si
, care va permite calculul direct al raportului μ al maselor, astfel ca μ < 1. Cunoscand μ si ![]() , se pot determina pulsatiile proprii ale sistemului cu
doua grade de libertate al absorbitorului dinamic. Masa utila fiind
anterior cunoscuta, se calculeaza masa suplimenrtara m1,
iar din conditia de acordare a absorbitorului,
, se pot determina pulsatiile proprii ale sistemului cu
doua grade de libertate al absorbitorului dinamic. Masa utila fiind
anterior cunoscuta, se calculeaza masa suplimenrtara m1,
iar din conditia de acordare a absorbitorului, ![]() , va rezulta rigiditatea elementului de legatura
dintre masa suplimentara si masa suplimentara.
, va rezulta rigiditatea elementului de legatura
dintre masa suplimentara si masa suplimentara.
Pentru evitarea cazului accidental
al apropierii frecventei excitatoare ω de una dintre pulsatiile
proprii ![]() sau
sau ![]() , se poate lega un amortizor in paralel cu arcul k2.
Prezenta amortizorului face ca sa se manifeste un raspuns
oscilatoriu al masei m2 la pulsatia excitatoare egala cu
, se poate lega un amortizor in paralel cu arcul k2.
Prezenta amortizorului face ca sa se manifeste un raspuns
oscilatoriu al masei m2 la pulsatia excitatoare egala cu ![]() . Reaamintim ca masa m2 inceteaza
sa oscileze la aceasta frecventa, daca absorbitorul
este acordat corect, iar sistemul nu prezinta amortizare.
. Reaamintim ca masa m2 inceteaza
sa oscileze la aceasta frecventa, daca absorbitorul
este acordat corect, iar sistemul nu prezinta amortizare.
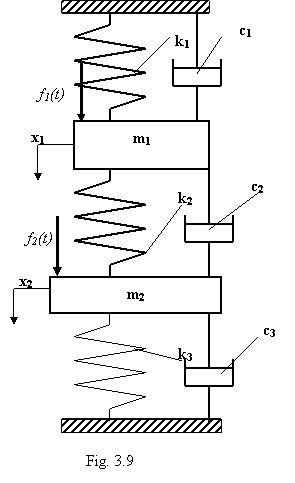
Vibratiile fortate amortizate ale sistemelor cu doua grade de libertate
Sistemele reale care se pot modela cu suficienta precizie ca ansamblu de doua mase concentrate legate prin elemente elastice intre ele si de suportul fix, sunt sisteme cu doua grade de libertate. Pentru limitarea amplitudinii oscilatiilor maselor aflate in stare de vibratie, sistemul poate fi prevazut cu amortizoare legate in paralel cu fiecare dintre resorturi, ca in figura 3.8. Fiecare dintre corpuri este actionat in mod independent de cate o forta excitatoare. Aceste forte au amplitudini diferite, dar sunt caracterizate de o pulsatie excitatoare comuna, ω.
Fig. 3.8
Masele in miscare
alternativa armonica au elongatiile instantanee ![]() si, respectiv,
si, respectiv, ![]() . Studiul miscarii are drept obiectiv determinarea
expresiilor acestor elongatii, ca functie de timp, plecand de la
premiza ca oscilatiile corpurilor sunt de tip armonic.
. Studiul miscarii are drept obiectiv determinarea
expresiilor acestor elongatii, ca functie de timp, plecand de la
premiza ca oscilatiile corpurilor sunt de tip armonic.
Aplicand metoda izolarii corpurilor (fig.3.9), pentru fiecare dintre ele se marcheaza fortele elastice si fortele de mortizare vascoasa din legaturi, forta excitatoare, rezultanta acestora fiind egala cu produsul dintre masa corpului si acceleratia imprimata lui.
Fig. 3.9
Ecuatiile de echilibru dinamic pentru sistemul corpurilor va fi:
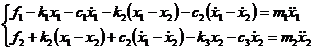
Sistemul de doua ecuatii
diferentiale are drept necunoscute deplasarile instantanee ![]() si
si ![]() ale corpurilor.
Fortele excitatoare vor fi termeni liberi intr-un astfel de model
matematic:
ale corpurilor.
Fortele excitatoare vor fi termeni liberi intr-un astfel de model
matematic:
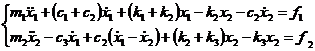
Sistemul de ecuatii diferentiale cu coeficienti constanti poate admite solutii de forma:
![]()
![]() ,
,
unde ![]() , cu
, cu ![]() , iar
, iar ![]() .
.
Elongatiile se pot exprima sub forma trigonometrica dupa cum urmeaza:
![]()
![]()
In acest fel se evidentiaza faptul ca fiecare solutie contine o componenta armonica de pulsatie b si o componenta de amortizare, al carei factor de amortizare este notat a. Pentru a putea impune ca elongatiile dub forma data sa fie solutii ale sistemului de ecuatii diferentiale, trebuie efectuate derivarile in raport cu timpul: