Teorema energiei electromagnetice

Teorema energiei electromagnetice

Aceasta teorema stabileste, in anumite conditii de mediu si pentru un sistem imobil de corpuri, aspectul energetic cantitativ al interactiunii corpurilor cu un camp electromagnetic determinand transformarile de energie care au loc atunci cand starea campului electromagnetic se modifica, sub forma localizarii ei (ca densitate de volum a energiei electromagnetice) si a propagarii ei (sub forma densitatii de suprafata a puterii electromagnetice radiate de camp).

In acest scop se considera ca intr-un domeniu marginit , unde "inchide" un volum v_W, se afla un sistem de corpuri imobile, ce "umplu" domeniul W, si un camp electromagnetic (caracterizat de marimile sale de stare si ). Pentru simplificare, se mai considera corpurile din W ca fiind izotrope si liniare (avand, deci, marimile de material e, si independente de camp), lipsite de polarizatie electrica permanenta () si magnetizatie permanenta (), cu starea lor electrica si magnetica descrisa, local, de marimile si . Starea acestui sistem -astfel precizat- este determinata de ecuatiile lui Maxwell (1.105M1), (1.105M2) si de ecuatiile (1.106M5) si (1.106M6), adica de :

, (E1)

, (E2)

, (E3)

. (E4)

Orice modificare procesuala de stare, survenita in sistemul electromagnetic precizat (de corpuri si camp electromagnetic in interactiune) nu se poate face decat printr-o variatie de energie a sistemului. In cazul unei modificari elementare a starii sistemului, variatia de energie aferenta lui va fi  in sensul: scaderea energiei campului electromagnetic din este egala cu energia electromagnetica transformata in alte forme de energie din plus energia electro-magnetica "radiata" , adica cea care "iese" prin suprafata ,ceea ce inseamna:

, (E5)

care se produce intr-un interval de timp elementar dt.

Sub forma de puteri, relatia (E5) devine:

, (E6)

in care este puterea transformata sub forma neelectromagnetica in domeniul W, iar este puterea electromagnetica transmisa prin invelisul S al domeniului W

In general, puterea electromagnetica se poate transforma in formele: putere calorica (prin efectul electrocineticii), puterea datorita miscarii corpurilor din W ("mecanica"), puterea necesara variatiei cu efect de intarziere - histerezis a polarizarii electrice si magnetice, puterea necesara reactiilor chimice etc. Deoarece s-a considerat, a priori, ca sistemul de corpuri este imobil, cu ε si μ constante (deci fara histerezis si fara schimbari structurale chimice), rezulta ca puterea se transforma numai in caldura, prin efect Joule, cu densitatea de volum , conform legii (1.103``), in orice punct , ceea ce permite sa se scrie:

. (E7)

Analizandu-se local procesele transformarilor energiei, pentru va trebui sa se determine densitatea de volum w (in Ws / m³) a energiei transformate, astfel ca pe ansamblul W energia transformata va fi:

(E8)                               ,

iar iradierea, in , a puterii electromagnetice prin densitatea de suprafata a acestei puteri (in W / m²), care se poate exprima printr-un vector , astfel incat fluxul lui prin suprafata de iradiere S este chiar scalarul P_S

(E9)                              ,

unde lui i se da numele de vectorul Poyting.

In aceste conditii, lucrandu-se cu distributiile si pe S, date de relatiile (E7), (E8) si definitia (E9), ecuatia de bilant (E6) a puterilor, in cazul unor tranformari de stare a sistemului electromagnetic considerat, ia forma:

(E10)        

al carui prim termen din membrul drept se poate scrie si astfel:

(E11)                    ,

in care a fost inlocuit prin expresia lui rezultata din ecuatia (E1).

Conform relatiei (9.32) din paragraful 9.1.2 (v. "Operatorul diferential - vectorial"), termenul are expresia:

,

care, introdusa in relatia (E11), conduce la:

.

Inlocuindu-se in aceasta ultima relatie, rot cu expresia sa (E2)  si -apoi- cu , conform ecuatiei (E4), iar cu , conform ecuatiei (E3), se obtine:

si -deoarece si (mediul fiind considerat liniar)- se mai poate scrie in continuare:

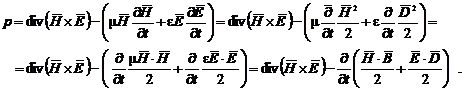
Calculandu-se, cu aceasta ultima expresia a lui p, puterea totala transformata in procesul de conductie in intreg volumul ocupat de domeniul W rezulta:

si, aplicandu-se formula lui Gauss-Ostrogradski (9.20), potrivit careia fluxul unui vector -aici - printr-o suprafata inchisa S este egala cu integrala de volum a divergentei acelui vector extins la volumul inchis de S = Fr W, se obtine in definitiv (prin transferarea termenului in membrul stang si inversarea, apoi, a membrilor intre ei):

.

Comparandu-se aceasta relatie finala cu relatia (E10), de la care s-a plecat, in conditiile in care si S sunt oarecari si identificandu-se termenii rezulta:

- expresia densitatii de volum a energiei electromagnetice din camp este:

, (1.111)

care are doua componente:

, (1.111`)

ce reprezinta densitatea de volum a energiei electrice si:

, (1.111``)

care este densitatea de volum a energiei magnetice;

- expresia densitatii de suprafata a puterii transmise (propagate) de campul electromag-netic, adica vectorul Poyting, este:

, (1.112)

puterea transmisa prin suprafata inchisa S de campul electromagnetic fiind -deci- fluxul acestui vector; . Daca, teoretic, campul se extinde la infinit, atunci suprafata S (care se inchide la infinit) poate fi o suprafata cvasiinchisa, deci -generalizand- S poate fi orice suprafata prin care se propaga campul electromagnetic, transportand energie.

Expresiile (1.111) si (1.112) reprezinta modele ale teoremei energiei electromagnetice.