Marimi fizice - Clasificarea marimilor fizice

Marimi fizice

Cercetarea sistemelor fizice si a fenomenelor fizice pe care le "gazduiesc",considerate -in procesul de cunoastere- ca obiecte ale gandirii, duce la constatarea ca aceste obiecte se diferentiaza intre ele atat calitativ cat si cantitativ, ceea ce a impus gasirea (introducerea) unor note (in sensul din "logica") si notiuni prin care sa se poata caracteriza si deosebi intre ele. O astfel de notiune este marimea, care se exprima lingvistic si se reprezinta simbolic prin procedee ale semioticii.

Astfel, prin activitatea de identificare a proceselor si de modelare a lor (adica de reprezentare matematica a relatiilor din sistemul obiect analizat) se stabilesc anumite proprietati (elemente-note specifice) diferite calitativ pe care le putem denumi marimi (sau specii de marimi - pentru a le preciza natura lor diferita) si anumite corelatii intre ele descrise matematic (modelate) prin legi -daca sunt deduse experimental sau prin teoreme, formule etc.- daca sunt stabilite deductiv din legi.

Pentru cunoasterea si modelarea fenomenelor fizice, concomitent cu sistemele fizice in care se manifesta, precum si pentru evaluarea raporturilor cauzaefect, nu este suficienta numai caracterizarea calitativa. Este necesara -in plus- o determinare cantitativa a relatiilor existente intre proprietatile obiectelor studiate, care sa conduca la corelarea aspectelor calitative ce delimiteaza obiectul (sistemul), la cuantificarea interactiunilor existente intre proprietatile sistemului-obiect si la precizarea evolutiei sistemului. Determinarea cantitativa a proprietatilor calitative ale unui sistem-obiect, adica a speciilor sale de "marimi" ce exprima aspecte de natura diferita, se face prin asa numitele marimi fizice. Desi notiunea de "marime" presupune -prin semantica ei- si o evaluare cantitativa, simplificand putin lucrurile vom defini o marime fizica prin acea marime (ca aspect calitativ) care poate fi determinata si cantitativ, adica o marime ce poate fi masurata si careia -prin masurare- i se poate atribui o "valoare" (mai exact o exprimare matematica, careia -prin abuz terminologic- i se spune "marime matematica"). Marimea matematica atasata -prin masurare- unei marimi (adica unei proprietati calitative), reprezinta o masura a marimii, cu valori in multimea valorilor marimii (continua - analogica sau discreta - numerica).

Sintetizand, o marime fizica contine in plus fata de marime (adica fata de aspectul calitativ al proprietatii pe care o exprima) si determinari cantitative (prin masurare) specifice, care reflecta o anumita manifestare interna existenta in mod natural.

De exemplu, in cazul unor procese mecanice putem constata ca diferite corpuri in "miscare" parcurg, fata de un sistem de referinta dat, "spatii" diferite in acelasi "interval de timp" (aceeasi "durata"). Aceasta este o analiza sumara a unui fenomen cu un specific al sau (zis mecanic), in care notiunile: miscare, spatiu si durata reprezinta aspecte (caracteristici) calitative, zise pe scurt marimi. Pentru o analiza de continut, cu evaluari cantitative care sa determine, in esenta sa, deplasarea corpurilor, se introduc noi marimi: viteza, acceleratia, masa, forta etc. Toate acestea (inclusiv spatiul si durata) sunt marimi fizice, deoarece ele sunt marimi masurabile, carora li se poate atasa cate o masura sub forma unor marimi matematice cu valori in multimea numerelor reale, cu precizarea ca marimile fizice atasate viteza, forta si acceleratia sunt marimi vectoriale, iar spatiul, durata si masa sunt marimi scalare.

Masurarea, prin care se determina cantitativ o marime fizica, este o activitate experimentala de tip informatic al carui scop este obtinerea unor date cantitative cu privire la proprietatile unui sistem-obiect si redarea lor intr-o forma potrivita pentru observator (utilizator). Semnificatia (interpretarea) pe care observatorul-utilizator o atribuie acestor date cantitative, prin intermediul conventiilor folosite pentru reprezentarea lor, constituie informatia care este necesara in procesul continuu de cunoastere, comunicare si conducere (decizie).

Determinarea cantitativa, prin masurare, a diverselor specii de marimi diferite calitativ, nu se poate realiza decat in raport cu marimi de aceeasi specie (aceeasi natura fizica) alese ca unitati cantitative, numite unitati de masura, fixate in mod conventional decat in cadrul unui sistem de unitati de masura coerent. O specie de marimi fizice este determinata atunci cand se indica procedeul de masurare, alegerea unitatii de masura fiind, in principiu, o optiune arbitrara. Dintre sistemele de unitati practice, unul -si anume Sistemul International de unitati (SI)- a fost adoptat pe plan mondial, la el aderand oficial majoritatea tarilor lumii. Deoarece, din anul 1961, SI a fost introdus si in Romania ca singur sistem de unitati de masura legal si obligatoriu, in cadrul acestui manual se vor folosi numai unitatile de masura ale SI, care se considera cunoscut de la cursul de Fizica.

Clasificarea marimilor fizice

Speciile de marimi fizice pot fi clasificate dupa numeroase criterii. Clasificarea speciilor de marimi prezinta importanta atat pentru optimizarea modelelor ce descriu fenomenele si sistemele fizice in cadrul unei teorii, cat si pentru aplicabilitatea unor categorii de metode de masurare.

Privite sub aspectul relatiilor dintre ele, marimile fizice (care stabilesc determinari cantitative pentru o proprietate comuna unei multimi de obiecte fizice) trebuie sa satisfaca in mod obiectiv cateva cerinte si anume:

- sa existe o relatie de echivalenta intre obiectele fizice avand aceeasi specie de marimi (proprietati), care este simetrica (in sensul ca daca un obiect fizic A este echivalent cu un alt obiect fizic B, atunci B este echivalent cu A), tranzitiva (adica: "A echivalent cu B" si "B echivalent cu C" "A echivalent cu C") si reflexiva (intotdeauna un obiect fizic A este echivalent cu el insusi). Exemple de echivalenta sunt: pentru proprietatea "forma geometrica" a obiectelor asemanarea geometrica, pentru proprietatea "lungime" a unor segmente coincidenta extremitatilor segmentelor, pentru marimea (proprietatea unor obiecte fizice) "temperatura" echilibrul termic a doua corpuri etc.;

- sa existe o relatie de ordonare intre doua din obiectele unei multimi de obiecte caracterizate de aceeasi specie de proprietati, care sunt neechivalente in sensul algebrei propozitionale binare (potrivit careia, o propozitie poate fi ori "adevarata" 1, ori "falsa" 0), adica "daca obiectul A este diferit de B" (ceea ce s-ar putea scrie AB) sa se poata stabili o relatie de ordonare in raport cu specia de marimi (proprietate) considerata, prin A>BB<A (adica asimetria, care se mai poate formula si prin A<B exclude B<A) si prin A>B si B<C A>C (adica tranzitivitatea). Ca exemplu, lungimile unor segmente de dreapta sunt ordonabile in raport cu relatia "mai lung decat" sau "mai scurt decat", care se obtine experimental suprapunandu-se segmentele de dreapta analizate, cu una din extremitati puse impreuna.

Revenind la clasificarea propriu-zisa a marimilor fizice, daca se ia drept criteriu felul cum se introduc ele in teorie, speciile de marimi fizice se impart in:

specii de marimi primitive care, intr-o teorie data, se introduc direct printr-un proces logic inductiv, insa pe cale experimentala si cu precizarea concreta a procedeului de masurare. Astfel, in teoria clasica a mecanicii s-au introdus ca marimi primitive: lungimea (distanta), durata (timpul), masa si forta, iar in termodinamica: caldura si temperatura. Marimile primitive nu se mai pot defini cu ajutorul altora, fara utilizarea experientei practice. Prin urmare, speciile de marimi primitive se introduc prin indicarea explicita a relatiilor de echivalenta si ordonare, precum si a procesului de comparare;

- specii de marimi derivate care -in cadrul unei teorii date pentru un domeniu de cercetare- se introduc prin analiza logica in functie de alte specii de marimi de referinta cunoscute, introduse in prealabil, fara a face uz de experienta. Asa de exemplu, in cinematica viteza e o marime derivata din speciile de marimi "lungime" () si "durata" () prin expresia , iar acceleratia este o marime derivata prin: etc. La introducerea unei specii de marimi derivate cu ajutorul unei relatii de definitie a valorilor ei numerice, pot aparea doua situatii speciale. Daca experienta arata ca aceste valori nu depind de valorile marimilor in functie de care au fost definite, dar depind de natura materialului sau obiectului la care se refera, marimea derivata nou introdusa se numeste (este) o marime de material, iar expresia prin care a fost definita este o relatie (lege, teorema etc.) de material (de exemplu, in domeniul Caldurii, coeficientul de dilatatie liniara al unui corp solid, notat cu , este o marime derivata definita prin expresia si deoarece practic ea nu depinde de lungimea l si -intr-un anumit interval- de temperatura , rezulta ca este o marime de material). Daca experienta arata ca aceste valori nu depind nici de valorile marimilor in functie de care au fost definite si nici de alte marimi sau conditii fizice (ca, de exemplu, valorile definite de raportul fortei de atractie gravitationala G, a doua puncte materiale prin produsul maselor lor m₁ si m₂, multiplicat cu patratul distantei r dintre ele, adica ), marimea derivata nou introdusa este o constanta universala (in exemplul dat, constanta de gravitatie f = 6,67 N∙m²∙kg^-2), iar expresia ei de definitie -in care se considera explicit independenta mentionata- este o lege generala (ca, de exemplu, legea atractiei universale: G = f m₁ m₂ / r²).

Calitatea de marime primitiva si derivata este relativa. Academicianul Remus Radulet, analizand sistemic relatia dintre numarul marimilor primitive si derivate dintr-o teorie aflata la un anumit nivel de dezvoltare, a aratat ca numarul marimilor primitive pentru studiul unui anumit fel de fenomene este un numar obiectiv. Intr-o anumita forma si stadiu al unei teorii se pot introduce anumite marimi ca primitive, iar in alta forma sau / si stadiu al teoriei ele ar putea apare ca derivate. Totusi, numarul speciilor de marimi primitive este invariabil in cadrul unui anumit domeniu de cercetare dat si la nivelul unei anumite teorii relativa la acest domeniu.

Dupa criteriul functiei pe care o au in legatura cauzala a fenomenelor, marimile fizice se clasifica in:  

- marimi de stare, adica acele marimi fizice prin care se poate descrie situatia manifestarilor ("starilor") care au loc intr-un sistem fizic izolat. Marimile de stare, prin modelele in care sunt incluse in cadrul unei teori, permit determinarea univoca a starii initiale si a evolutiei in viitor, pe baza principiului cauzalitatii (efectcauza). De exemplu, in Mecanica clasica starea unui corp punctiform cu masa m (asa-numitul punct material) este complet determinata de marimile de stare numite impuls si raza vectoare;

- marimi de proces, adica marimile fizice prin care se descrie interactiunea unui sistem fizic cu alte sisteme sau trecerea sa dintr-o stare in alta. Luand exemple tot din Mecanica clasica, marimile forta 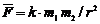si lucru mecanic sunt marimi de proces deoarece forta descrie interactiunea unui punct material cu alte corpuri, iar lucrul mecanic caracterizeaza trecerea punctului material dintr-o stare in alta cand parcurge o traiectorie c intre doua puncte a si b.

Dupa rolul pe care il au in alcatuirea sistemelor de unitati de masura, speciile de marimi se clasifica in:

- marimi fundamentale, care sunt acele marimi ale caror unitati de masura se aleg independent, prin indicarea reprezentarii lor in mod concret (prin masuri, etaloane, relatii de calcul ce definesc unitatea etc.). In Sistemul International de unitati de masura, marimile fundamentale sunt: lungimea, masa, durata, temperatura termodinamica, intensitatea luminoasa,  intensitatea curentului electric s.a.;

- marimi secundare care sunt acele marimi ale caror unitati de masura rezulta univoc din modelele ce includ speciile de marimi fundamentale, in functie de unitatile de masura independente ale acestor specii. Asa sunt, de exemplu: viteza, acceleratia, lucrul mecanic, fluxul luminos, caldura etc. etc.

Din punctul de vedere al modelarii sistemelor, marimile susceptibile de a fi masurate si evaluate valoric (deci marimile fizice) se pot clasifica si dupa marimile matematice care le sunt atasate. In activitatea de modelare si de masurare, fiecarei specii de marimi fizice ii este atasata o asa-numita marime matematica , prin aplicatia , care poate fi: scalara, vectoriala sau tensoriala. De exemplu: lungimea, temperatura, debitul (masic sau volumic) etc. sunt reprezentabile prin scalari (X_mR), pozitivi sau negativi (iar masa, durata s.m.a. prin scalari pozitivi); viteza unui punct material, acceleratia, forta etc. sunt reprezentabile prin vectori(cu valoarea absolutaR); pe cand starea de tensiune dintr-un punct al unui corp solid deformabil elastic este reprezentata printr-un tensor simetric. Tensorul este o entitate matematica prin care fiecarui punct dintr-un sistem de referinta n-dimensional i se asociaza o matrice n^m ordonata de valori reale, ce exprima cantitativ (valoric) o marime fizica. Aici m este ordinul tensorului, astfel ca intr-un sistem de referinta cartezian tridimensional (n = 3), Ox, Oy si Oz, daca m = 0 tensorul este de ordinul zero (adica scalarul), daca m = 1 tensorul este de ordinul unu (adica vectorul) si daca m = 2 tensorul este de ordinul doi (adica tensorul propriu-zis). Astfel, in tridimensional, cu n = 3, scalarul se reprezinta printr-o matrice cu un singur element (n^m = 3⁰ =1) care este un numar real, vectorul prin matricea cu 3¹ = 3 elemente (X_x , X_y si X_z - fiecare fiind un numar real) si tensorul prin 3² = 9 elemente (toate, de asemenea, numere reale). De aceea, la evaluarea unei marimi fizice prin masurare se vor determina pentru acea marime unu, trei sau noua marimi scalare, in functie de felul marimii matematice care ii este atasata.

Din punctul de vedere al aditivitatii (insumarii) lor, marimile fizice pot fi: aditive, indirect aditive si neaditive. Aditivitatea este proprietatea unei marimi fizice de a putea fi evaluata prin insumarea directa a unor "portiuni" ale acelei marimi, masurate separat si direct, iar marimile care au aceasta insusire se numesc marimi direct aditive (asa sunt marimile: lungimea, masa, debitul instantaneu al unui fluid printr-o conducta s.a.). La aceasta specie de marimi, conventia de scara (de indicare a valorii) se reduce la relatia de proportionalitate dintre marimea aditiva (X) si unitatea sa de masura (u_m), adica X = X_m u_m, factorul de proportionalitate X_m reprezentand chiar valoarea marimii. De aceea unitatea de masura u_m se stabileste conventional, prin specificarea etalonului, fiind suficient un singur etalon pentru construirea intregii scari (datorita proprietatii de aditivitate). La marimile neaditive, intreaga scara a aparatelor prin care se determina valoarea lor trebuie stabilita conventional, prin fixarea unui numar suficient de repere si a modului de interpolare intre ele (un exemplu este scara internationala practica de temperatura). Exista marimi care nefiind direct aditive se numesc marimi indirect aditive daca pot fi exprimate  valoric in functie de alte marimi aditive. Asa sunt majoritatea marimilor de material, ca - de exemplu - coeficientul de dilatatie liniara termica a unui material , ce se exprima in [1/grd] cu expresia: , pentru a carui determinare se confectioneaza (din materialul analizat: alama, aliaj fier-nichel, plumb etc.) o bara cu lungimea l₀ la temperatura (sa zicem de 20˚C), cu aria sectiunii transversale a relativ mica (adica), se incalzeste uniform la o temperatura > (daca = 20˚C, se ia = 120˚C ÷ 400˚C) si se masoara la aceasta temperatura lungimea la care a ajuns bara; atunci, deoarece lungimea si temperatura sunt marimi direct aditive, coeficientul de dilatatie liniara se determina indirect, facandu-se calculul: [1/grd].

Din punctul de vedere al felului cum apar diferitele marimi fizice in modelele unei teorii relative la o specie de fenomene, marimile pot fi:

- marimi de grad 1, adica marimile care in modelele lor de definitie figureaza ca termeni de gradul unu (de exemplu, in cazul unui punct material cu masa m: viteza , impulsul , acceleratia , forta , lucrul mecanic etc.);

- marimi de grad 2, adica marimile care in modelele teoriei apar prin produse sau sume de produse a cate doua marimi de grad 1 (de exemplu, in cazul punctului material, energia sa cinetica este o marime de grad 2);

- marimi de grad 0, adica marimile care in modelele teoriei se definesc prin raportul dintre doua marimi de grad 1 sau grad 2 (considerandu-se tot exemplul punctului material, masa sa m este o marime de grad 0, fie daca se defineste prin raportul , fie prin raportul ).

Clasificarea marimilor dupa grad prezinta importanta in special in legatura cu alegerea celei mai adecvate tehnici de masurare (din punctele de vedere ale: preciziei, simplitatii, duratei de masurare s.a.).