|
|
|
Cuantificarea MARIMILOR observabile
Din cele discutate in paragrafele anterioare se poate trage concluzia ca din punct de vedere al mecanicii cuantice sunt foarte importante valorile posibile pentru o observabila. Daca aceasta observabila este cuantificata, mecanica cuantica trebuie sa explice cuantificarea.
In cazul energiei, Schrodinger a aratat ca energiile posibile se obtin din rezolvarea ecuatiei care-i poarta numele:
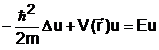
Din punct de vedere matematic, ecuatia precedenta este o ecuatie cu valori proprii de forma:
(4.24)
unde H este un operator:
(4.25)
care se aplica functiei u, iar E este un numar. H se numeste operatorul energiei.
Pe de alta parte, clasic, energia poate fi exprimata astfel:
Deoarece un sistem cuantic poate avea valori determinate ale patratului momentului cinetic orbital si ale uneia din proiectiile sale pe axele de coordonate, se determina valorile proprii corespunzatoare. Sistemul de coordonate mai bine adaptat pentru calculele care urmeaza este sistemul de coordonate sferice. In acest sistem de coordonate, operatorii momentului cinetic orbital au expresiile :
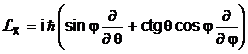
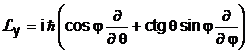(4.30)
si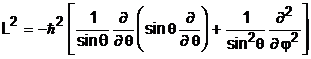 
(4.31)
Pentru a gasi valorile proprii ale proiectiei momentului cinetic pe axa z se va rezolva ecuatia:
1. Ecuatia de continuitate in mecanica cuantica
In mecanica cuantica se poate deduce o ecuatie de aceeasi forma cu ecuatia de continuitate intalnita in fizica clasica. Pentru a deduce aceasta ecuatie vom scrie ecuatia Schrodinger si expresia complex conjugata, care este verificata in acelasi timp de functiile de unda:
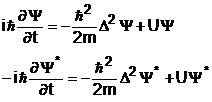(4.34)
Inmultind
la stanga prima relatie cu 
pe cea de a doua cu 
si
scazandu-le, rezulta:
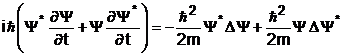
2. Particula intr-o groapa de potential cu pereti infiniti
Aproximatia unei particule care se gaseste intr-o groapa de potential isi gaseste aplicatii in studiul electronilor dintr-un metal, in studiul particulelor , etc.
Groapa de potential cu pereti infiniti (figura 4.3) este definita prin urmatoarele valori ale energiei potentiale:
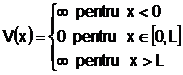(4.37)
unde L este largimea gropii.
Groapa
de potential imparte spatiul in trei regiuni, dar ecuatia
Schrodinger se va integra pe intervalul (
). Cand x < 0 sau x > 0, 
, deoarece probabilitatea de a gasi particula in afara
gropii de potential este nula.
