|
|
|
Difuzia particulelor
Exista doua moduri de transfer a materiei printr-o suprafata: convectia, atribuita unei deplasari globale a materiei si difuzia (in absenta unei deplasari globale).
1. Legea lui Fick
Vom
nota 
numarul de
particule macroscopice, de viteza medie 
, care traverseaza elementul de suprafata 
, in timpul dt, unde 
este versorul normalei
exterioare la dS. reprezinta
numarul de particule continute in volumul cilindric de baza dS
si de inaltime 
(figura 1.3).
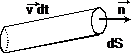
Fig. 1.3
Daca
este numarul de
particule pe unitatea de volum, in punctul definit de vectorul de pozitie 
, la momentul t, vom numi flux de particule cantitatea:
(1.42)
sau
unde s-a notat
(1.43)
vectorul densitate de curent de particule.
Fluxul total prin suprafata S se obtine integrand:
Experimental, s-a dedus legea lui Fick, care traduce, in aproximatia liniara, proportionalitate dintre densitatea volumica de particule si concentratie:
(1.44)
Semnul
minus din relatia (1.44) arata ca vectorul densitate
volumica de particule este dirijat spre regiunile cu densitate mica
de particule. Marimea D, numita coeficient de difuzie,
este o marime pozitiva, cu unitatea de masura in S.I. 
. Limitarile legii sunt observate pentru
concentratii prea mici sau prea mari.
2. Ecuatia difuziei
Daca N este numarul de particule dintr-un volum delimitat de suprafata S, variatia acestuia intre momentele t si t+dt este:
unde 
este numarul de
particule primit (algebric) prin suprafata S, iar 
este numarul de
particule produse (algebric) in sistem (prin reactii chimice sau de
recombinare).
In aceste conditii se poate scrie:
, 
si 
unde 
reprezinta
productia de particule pe unitatea de volum si de timp.
Tinand sama ca
se obtine, aplicand teorema Gauss, relatia:
(1.45)
expresie ce reprezinta ecuatia de continuitate relativa la numarul de particule.
Pentru a obtine ecuatia difuziei, este suficient sa se inlocuiasca in (1.45), relatia (1.44). Se obtine:
(1.46)
Expresia (1.46) reprezinta ecuatia difuziei. Este de remarcat faptul ca expresia nu este invarianta la schimbarea lui t in -t. Se spune ca fenomenul de difuzie este fundamnetal ireversibil.
