
|
|
|
Tipurile fundamentale de indici ai preturilor
In teoria si practica economica, in functie de ponderile folosite (din perioada de baza sau curenta), precum si in functie de expresia matematica a indicilor, pana in prezent sunt cunoscute si aplicate trei tipuri fundamentale de indici purtand numele personalitatilor care le-au creat si anume: Laspèyres, Paasche si Fisher.
A. Indicele Laspèyres (IL) - este un indice agregat de preturi, care utilizeaza ca ponderi ale preturilor, cantitatile de produse vandute sau consumate in perioada de baza. Esential in aceasta conceptie este pastrarea bazei de comparatie (q) neschimbata. Formula de calcul este:
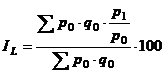 sau
sau 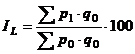 (6.7)
(6.7)
in care:
![]() = valoarea produselor vandute in anul de baza, in
preturile anului de baza;
= valoarea produselor vandute in anul de baza, in
preturile anului de baza;
![]() = valoarea
cantitatilor de produse vandute in anul de baza in
preturile anului curent;
= valoarea
cantitatilor de produse vandute in anul de baza in
preturile anului curent;
![]() = indicii individuali
ai preturilor nominale ale produselor cuprinse in calcul
= indicii individuali
ai preturilor nominale ale produselor cuprinse in calcul
![]() = valoarea
recalculata a cantitatilor de produse vandute in perioada de
baza in preturile anului curent.
= valoarea
recalculata a cantitatilor de produse vandute in perioada de
baza in preturile anului curent.
Desi este usor de calculat, prin simplitatea si constanta bazei, acest tip de indice are o aplicabilitate limitata, deoarece foloseste pentru ponderarea preturilor aceleasi cantitati de produse, volumul si structura productiei din perioada de baza ramanand neschimbate. Dar, in conditiile introducerii rapide a progresului tehnic, structura indicelui se invecheste destul de repede, necesitand revizuirea sistemului de ponderare la perioade foarte scurte de timp. In tara noastra, acest tip de indice este aplicat, in special, la determinarea dinamicii volumului fizic al productiei, existand insa si tendinta utilizarii lui prin calcularea indicilor preturilor produselor ce fac obiectul productiei marfa agricole.
B. Indicele Paasche (Ip). Acest tip de indice utilizeaza pentru ponderare, intotdeauna, cantitatile produselor din perioada curenta. Fiind conceput a se determina cu ajutorul structurii noi a productiei si a consumului, el are o aplicabilitate mai mare fiind utilizat pe larg in tara noastra. Formula de calcul este:
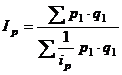 sau
sau 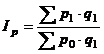 (6.8)
(6.8)
in care:
![]() = valoarea cantitatilor produse din anul curent,
exprimata in preturile anului curent;
= valoarea cantitatilor produse din anul curent,
exprimata in preturile anului curent;
![]() = valoarea cantitatilor produse din anul curent,
exprimata in preturile anului de baza;
= valoarea cantitatilor produse din anul curent,
exprimata in preturile anului de baza;
![]() = modificarea preturilor nominale ale produselor in
perioada curenta p0 (1) fata de cea de baza (0).
= modificarea preturilor nominale ale produselor in
perioada curenta p0 (1) fata de cea de baza (0).
Principalele avantaje ale acestui indice sunt: este simplu si usor de inteles; poseda proprietatea de agregare, adica indicii individuali (Ip) pot fi insumati; prin folosirea ponderilor din perioada curenta asigura actualizarea structurii productiei, precum si a consumului intermediar al populatiei si, totodata, da posibilitatea calcularii economiilor efective sau platilor suplimentare, pe care le realizeaza populatia ca urmare a reducerii sau majorarii preturilor.
Insa aplicarea acestui indice presupune schimbarea continua a ponderii de calcul, ceea ce complica acest calcul si-i restrange aplicabilitatea. Este necesara reinnoirea sa in fiecare an (fiind de fapt un indice agregat cu ponderi variabile), ceea ce conduce la un sistem informational complicat si la dificultati in calcularea lui. Principalul neajuns tine de continut. Ponderile perioadei curente care se folosesc in structura sa reflecta structura actuala a consumului. In aceasta structura, importanta si greutatea specifica a diverselor marfuri poate diferi substantial de cea existenta in structura consumului din anul de baza. Ponderand preturile perioadei de baza cu produsele in volumul si structura actuala, numitorul fractiei apare, in general, supraevaluat si, in consecinta, indicele va reflecta o miscare de preturi mai mica decat cea reala.
Cu ajutorul indicilor de pret de tip Laspèyres si Paasche se procedeaza la transformarea dinamicii veniturilor nominale ale populatiei in dinamica veniturilor reale ale acesteia, adica a puterii de cumparare, exprimata in indicele volumului fizic al consumului de bunuri si servicii:
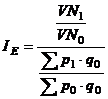 (6.9)
(6.9)
in care:
IE = indicele veniturilor reale in perioada curenta fata de perioada de baza;
VN1 = veniturile nominale ale perioadei ale perioadei (1) care se cheltuiesc integral pentru bunuri si servicii exprimand cumpararile Q1 la preturile p1;
VN0 = veniturile nominale ale perioadei ale perioadei (0) care se cheltuiesc integral pentru bunuri si servicii exprimand cumpararile Q0 la preturile p0;
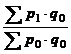
Prescurtat, se poate scrie ![]() , ceea ce se interpreteaza astfel: daca
preturile cantitatilor bunurilor si serviciilor consumate
in perioada curenta cresc mai repede decat cresc veniturile nominale in
acelasi interval de timp, puterea de cumparare scade, si invers.
, ceea ce se interpreteaza astfel: daca
preturile cantitatilor bunurilor si serviciilor consumate
in perioada curenta cresc mai repede decat cresc veniturile nominale in
acelasi interval de timp, puterea de cumparare scade, si invers.
Raportul dintre indicele veniturilor nominale si indicele preturilor de tip Paasche reprezinta indicele volumului fizic al consumurilor de tip Laspèyres:
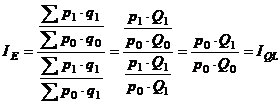 (6.10)
(6.10)
C. Indicele Fisher (IF). Are cea mai mare aplicabilitate pe plan mondial. Formula sa de calcul reprezinta media geometrica a indicilor Laspèyres si Paasche, adica:
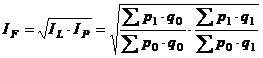 (6.11)
(6.11)
Fiind media geometrica a celor doi indici prezentati, acest indice inlatura, in buna masura, neajunsurile celorlalti. De asemenea, acest procedeu este cel mai elastic instrument de comparatie, deoarece media geometrica prezinta mai multa stabilitate, reflectand mai fidel evolutia reala a fenomenului economic.