Gestionarea portofoliilor bancare - rentabilitatea si riscul portofoliilor, modelul diagonal de selectie a portofoliului, evaluarea activelor financiare cu ajutorul modelului a.p.t.

GESTIONAREA PORTOFOLIILOR BANCARE

1. RENTABILITATEA SI RISCUL PORTOFOLIILOR

1.1. RENTABILITATEA SI RISCUL UNUI PORTOFOLIU DE DOUA TITLURI FINANCIARE

Un portofoliu de doua titluri se constituie in proportii diferite de participare a unuia si a altuia dintre ele (x si y). O performanta superioara a acestui portofoliu se poate obtine la o anumita combinatie optima de participare a celor doua titluri.

Rentabilitatea portofoliului (R_p) este media ponderata a rentabilitatilor separate (medii) ale celorlalte doua titluri R_i si R_j :

R_p = x * R_i + y * R_j

in care x + y = 1

Rentabilitatea portofoliului este, deci, direct proportionala cu rentabilitatile titlurilor componente dar si cu ponderea de participare a fiecarui titlu la compunerea portofoliului. Pentru a creste rentabilitatea portofoliului ar fi suficient sa crestem ponderea titlului cel mai rentabil. Dar aceasta crestere de remtabilitate este insotita si de cresterea riscului.

Riscul atasat unui portofoliu (s_p²) este o combinatie intre dispersiile ( s_I² si s_j²) fiecarui titlu component, in functie de ponderile de participare la formarea portofoliului :

s_p² = x² s_I² + y² s_j² + 2xy s_ij

in care sij = covariatia dintre abaterile probabile ale rentabilitatilor R_i si R_j in raport cu speranta lor matematica.

N

s_ij SProb_s* R_is- E R_i R_js-E R_j

s=1

unde s = 1,2,3,,N stari posibile ale naturii in perioada de previziune.

Prob_s= probabilitate asociata fiecarei stari posibile ale naturii.

Covariatia s_ij se poate determina si pe baza coeficientului de corelatie (C_ij) si a abaterilor medii patratice ale celor doua titluri (s_i si s_j

s_ij = C_ij x s_i x s_j

Tipuri de corelatii rentabilitate risc intr-un portofoliu de doua titluri

In raport cu coeficientul de corelatie C_ij, intre rentabilitatile celor doua titluri se pot identifica trei tipuri de corelatie extreme: pozitiva, zero si negativa.

Corelatia strict pozitiva este aceea cu coeficientul de corelatie egal cu unu (C_ij = 1), in care unei cresteri a rentabilitatii primului titlu 'i' ii corespunde o crestere, in aceeasi masura, a rentabilitatii celui de-al doilea titlu 'j'. Riscul portofoliului acestor titluri, total dependente unul de celalalt, este cel mai mare (C_ij = 1); la fiecare crestere a rentabilitatii portofoliului are loc o crestere direct proportionala a riscului. Drept urmare, pe dreapta de corelatie rentabilitate risc, a unui astfel de portofoliu, nu vom gasi vreo combinatie de titluri mai performanta decat detinerea integrala a unuia sau altuia dintre titluri.

R_p/s_p² Ri/s_p² R_j/s_p² = constant

Rentabilitate Rentabilitate

E R_j j

R_j

E R_i i

R_i

timp s_i² s_j² risc

Corelatia strict pozitiva intre doua titluri ce compun un portofoliu

Corelatia nula (zero) este egala cu coeficientul zero al corelatiei (C_ij = 0), in care rentabilitatile celor doua titluri variaza in timp total independent. Absenta vreunei corelatii face ca riscul portofoliului sa se diminueze :

s_p² = X² s_i² + Y² s_j²

intrucat 2xy s_ij = 2xy c_ij s_is_j = 0

cu c_ij = 0

Rentabilitate           Rentabilitate

E R_j j

R_i

R_p

M

R_j E R_i i

Timp s_i s_j Risc

Corelatia a doua titluri independente

Ca urmare a diminuarii portofoliului de titluri independente, exista o combinatie optima intre titlurile componente in care performanta portofoliului este maxima DR_p/Ds_p² = max

Din punctul i pana in punctul M avem combinatii, intre titlurile 'i' si 'j' care conduc progresiv spre cresterea rentabilitatii portofoliului, in conditiile diminuarii riscului acestuia. Punctul M este performanta maxima a portofoliului, dar cu asumare de riscuri din ce in ce mai mari.

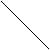
Corelatie strict negativa, cu coeficientul de corelatie egal cu limita sa inferioara (c_ij = -1), este aceea in care unei cresteri a rentabilitatii titlului 'i' ii corespunde o scadere in egala masura, a rentabilitatii titlului complementar 'j'.

Rentabilitate Rentabilitate

R_j R_j j

M

R_i i

R_i

Timp s_is_j Risc

Riscul unui astfel de portofoliu de titluri , total dependente negativ, este cel mai mic. O combinatie optima a celor doua titluri conduce chiar la risc zero al portofoliului .

s_p² = x² s_i² + y² s_j² + 2xy s_ij

in care : s_ij = (-1) s_is_j

Intr-o combinatie optima (M) primii doi termeni ai ecuatiei sunt egalati (negativ) de termenul final, deci s_p² = 0. Trebuie remarcat ca in general, corelatiile negative, sunt foarte rare. Cele mai multe sunt cele slab pozitive.

1.2. RENTABILITATEA SI RISCUL UNUI PORTOFOLIU FORMAT DIN 'N' TITLURI FINANCIARE

Rentabilitatea unui portofoliu de 'n' titluri este media ponderata a rentabilitatilor medii (R_i) ale titlurilor care-l compun. In mod necesar acesta se va afla intre limitele privind cea mai buna si cea mai slaba rentabilitate a titlurilor care compun portofoliul, in functie de ponderile ce se acorda titlurilor componente (X_i) :

R_p = a Xi Ri

unde i = 1,2,.,n feluri de portofoliu.

Rentabilitatea portofoliului este deci independenta de corelatiile dintre rentabilitatile individuale ale titlurilor componente . Nici o combinatie a titlurilor nu va duce la o rentabilitate a portofoliului superioara celei mai mari rentabilitati individuale.

In conformitate cu avantajul diversificarii unui portofoliu se poate aprecia ca riscul acestuia depinde, in primul rand, de numarul de titluri care il compun (ca urmare a compensarii variatiillor contrare ale rentabilitatii acestor titluri). In acelasi timp, este semnificativa structura portofoliului: daca titlurile au ponderi relativ egale in compunerea portofoliului, atunci riscul acestuia este mai mic decat atunci cand o actiune detine 90% din portofoliu, iar celelalte actiuni ocupa restul de 10%. Pe de alta parte, un portofoliu, compus din actiuni ale unor societati recunoscute si importante, va fi mai putin riscant decat un portofoliu ce cuprinde titluri ale unor societati mici si care nu coteaza la bursa.

In sfarsit, un portofoliu diversificat si pe mai multe ramuri economice va fi mai putin riscant decat portofoliu care cuprinde titluri dintr-o singura ramura.

In sinteza, riscul unui portofoliu depinde de trei factori:

1. riscul fiecarei actiuni inclusa in portofoliu;

2. gradul de independenta a variatiilor actiunilor intre ele;

3. numarul de titluri din portofoliu.

Riscul acestuia , poate sa rezulte din urmatoarea matrice a dispersiilor (s_ii) si a covariatiilor (s_ji) rentabilitatilor titlurilor componente:

s_p² a X_i² s_I² aa X_i X_j s_ji

I=1 ij

n dispersii (n² - n) covariatii

Riscul portofoliului de 'n' titluri reprezinta deci suma tuturor combinatiilor posibile intre rentabilitatile titlurilor componente (inclusiv propriile dispersii), in functie de ponderile de participare a titlurilor la compunerea portofoliului.

2.MODELUL DIAGONAL DE SELECTIE A PORTOFOLIULUI

2.1. IPOTEZELE MODELULUI DIAGONAL

In elaborarea modelului sau, Sharpe porneste de la o intuitie fireasca pentru un cercetator atent: ansamblul covariatiilor in general pozitive, din cadrul riscului unui portofoliu poate avea un factor comun de determinare. Acest factor comun poate fi un indicator macroeconomic care influenteaza in mod substantial piata titlurilor financiare (indice bursier, rata de dobanda, PIB, etc.).

Pornind de la aceasta ipoteza, in cea mai mare parte realista (pe o piata financiara activa), putem afirma ca rentabilitatea fiecarui titlu financiar este in mare masura explicata (determinata) de evolutia factorului comun (a indicelui bursier R_M, spre exemplu) ca variabila exogena: R_i=f(R_M). Toti ceilalti factori care ar mai putea influenta rentabilitatea R_i sunt considerati endogeni si vor determina variatia neexplicata prin R_M , respectiv riscul specific al titlului 'i'.

Ne propunem o mica paranteza prin care afirmam importanta capitala a modelului de piata (single index model or one factor model, in engleza). Identificarea acestui model si testarea validitatii corelatiei titlurilor 'i' cu factorul de piata 'M' au permis elaborarea modelului diagonal. La randul lui, modelul diagonal a inspirat constructia unui model celebru (CAPM) de evaluare a activelor financiare ca norma de remunerare de catre piata a investitiei in aceste active. In continuare, CAPM a inspirat un alt, nu mai putin celebru, model multifactorial (APT) de evaluare a activelor financiare. si lantul efectelor de propagare se continua in estimarea costului capitalului, in modelul multiperiodic, ca sa nu amintim decat pe cele mai actuale preocupari.

Putem afirma ca rentabilitatea unui titlu financiar depinde liniar de rentabilitatea de piata R_M ecuatia dreptei de regresie putand fi scrisa sub urmatoarea forma

R_i=a_i b_i*R_M+e_I

in care,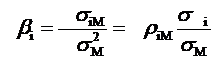

N

unde s_iM SProb_s* R_is- E R_i R_js-E R_M

s=1

unde s = 1,2,3,,N stari posibile ale naturii in perioada de previziune.

Prob_s= probabilitate asociata fiecarei stari posibile ale naturii.

Aceasta corelatie are anumite proprietati, foarte utile in abordarile ulterioare:

Factorul rezidual e_i ,rezultat prin aplicarea metodei de regresie a celor mai mici patrate, este deci expresia riscului specific (neexplicat prin factorul comun R_M). Speranta sa matematica este nula (proprietate dobandita prin metoda celor mai mici patrate), iar dispersia sa se presupune a ramane constanta (aceeasi supozitie ca si constanta de legaturi dintre R_i si R_M). Exprimand riscul specific al titluluui 'i' fara nici o legatura cu riscul celorlalte titluri sau cu riscul sistematic (de piata), este admisa cu temei teza independentei factorului e_j fata de ceilalti factori e_j si fata de cel al pietei (in consecinta, r_ij r_iM=0

Inca o ipoteza si trecem la virtutile modelului de piata care l-au facut atat de util in elaborarea modelelor viitoare. Se considera ca toate corelatiile s_iM (intre R_i, fiecare in parte, si R_M ca factor comun) urmeaza o lege normala bivariabila: variatia R_M determina, in marimi diferite (specifice fiecarui titlu), variatia sistematica a R_i; la randul ei, variatia R_i va induce o contributie specifica (particulara a titlului 'i') la variatia totala a R_M. Ambele variatii ale R_i si R_M urmeaza o lege normala (bivariabila, in cazul nostru). Daca toate covariatiile s_iM se inscriu in aceasta lege de distributie, atunci pentru definirea lor este suficienta cunoasterea urmatoarelor informatii: E_i, s_i², E_M, s_M², si r_iM (in total, 3n informatii despre titlurile i si 2 informatii despre factorul comun -indice bursier - , deci 32n+2 strict inferior lui 2n+n(n-1)/2 ).

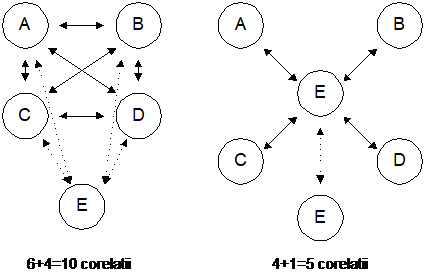
Exemplu: Daca luam patru titluri (A, B, C, D) vom observa ca fara a introduce acest factor comun identificarea legaturilor dintre rentabilitatile lor se face apel la sase relatii (s_AB s_AC s_AD s_BC s_BDs_CD), iar in modelul Sharpe la numai patru (s_AM s_BM s_CM s_DM). Daca mai adaugam un titlu (E) vor fi necesare +4=10 realtii in fara a introduce foctorul comun fata de 4+1=5 relatii in modelul Sharpe .

Reprezentarea legaturilor intre rentabilitatile R_i si R_M

2.2. EXPRIMAREA RISCULUI PORTOFOLIULUI IN MODELUL DIAGONAL

In aceste conditii de simplificare a intercorelatiilor dintre titlurile "I", riscul total al fiecaruia se va defini in raport cu riscul de piata (s_M²) si cu riscul specific (s²_ei

prin ridicare laprin ridicare laegale cu 0

patrat expresia patrat expresiprin ipoteza

devine s_M² devine s²_eI

In consecinta, riscul total al titlului i dobandeste, in modelul simplificat, o noua formulare:

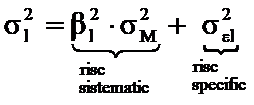
Suntem acum pregatiti sa abordam modelul diagonal de selectie a portofoliului. Deci, mai intai sa redefinim riscul portofoliului si apoi sa urmarim minimizarea lui. In forma sa simplificata, riscul total al portofoliului se va defini in functie de corelatiile titlurilor i cu M si nu cu perechile j

In care fiecare abatere se rescrie dupa modelul de piata:

Deci,

=0 =0 =0

In consecinta, pentru oricare i si j=1,2,..,n:

Cu aceste expresii noi ale riscului s_l² si ale covariatiilor s_ij , riscul total al portofoliului (s_p²) se rescrie astfel:

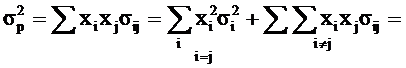
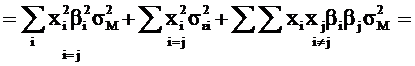
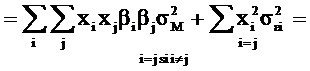
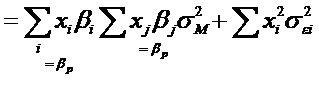
Expresia riscului total al portofoliului in modelul diagonal evidentiaza cele doua componente ale riscului: sistematic () si specific

Simplificarea este acum evidenta intrucat primul termen se obtine ca produs intre vectorii coloana x_I si b_i, pe de o parte; si variabila exogena s_M², iar al doilea termen se obtine ca produs intre vectorii linie si coloana x_I si matricea diagonala s_el³

Problema de rezolvat in modelul diagonal este urmatoarea:

stiind ca:   

Recurgerea la functia Lagrange si cautarea minimului ei conduce la urmatorul sistem matriceal pentru determinarea frontierei eficiente:

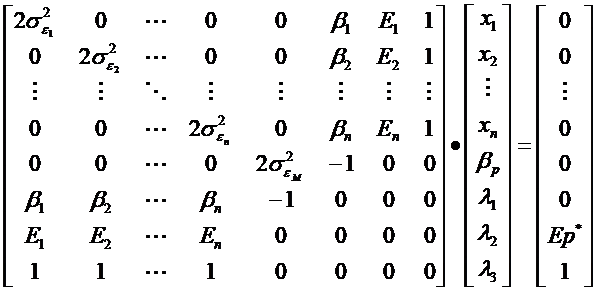
W   X K

Compozitia portofoliilor eficiente cu risc minim, la o speranta de rentabilitate data (dorita = E*p), va fi solutia la sistemul matriceal:

X=W^-1*K.

2.3.       APLICATIE A MODELULUI DIAGONAL

Scopul acestei aplicatii este identificarea procedurii operationale a modelului diagonal si nu economia de informatii necesare. Economia de informatii nu devine evidenta decat la portofolii formate din cel putin 5 titluri. La trei titluri avem nevoie chiar de mai multe informatii decat in modelul de baza .

In exemplu nostru estimarea vom estima un portofoliu de trei titluri (o actiune , o prima dubla , si o obligatiune) prin anticiparea pentru toata perioada viitoare a patru stari ale naturii:avant economic , crestere economica , stabilitate si recesiune.Astfel se dau rentabilitatile estimate ale celor trei titluri corespunzatoare fiecarei stari ale naturii si probabilitatile asociate fiecarei stari a naturii :

La aceste trei titluri initiale asociem valorile rentabilitatii (R_M) si riscului (s_M²) estimate pe ansamblul pietei financiare (indicele bursier) in aceleasi stari probabile ale naturii. Aceste valori centrale de referinta ne vor permite stabilirea corelatiei titlurilor initiale cu indicele pietei financiare si-n continuare selectia portofoliilor eficiente conform modelului diagonal.

Prin utilizarea modelului de piata vom determina intr-o prima faza parametrii sistemului de ecuatii de regresie liniara (a_i si b_i

Incercand acum sa estimam rentabilitatile titlurilor individuale () in functie de rentabilitatea pietei pentru fiecare stare a naturii () vom fi in masura sa determinam riscul specific al titlurilor (s_el²

Problema de minimizare a riscului portofoliului in modelul diagonal va avea urmatoarea forma concreta:

Min (x₁²*3,8465+x₂²*2,8866+x₃²*2,387)

+(x₁*1,457+x₂*0,65+x₃*0,92)²*3,09 ²

stiind ca:

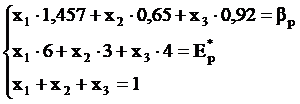
Utilizarea functiei Lagrange si minimizarea ei conduce la urmatorul sistem matriceal al derivatelor partiale in functie de x₁, x₂, x₃, b_p l₁ l₂ l₃

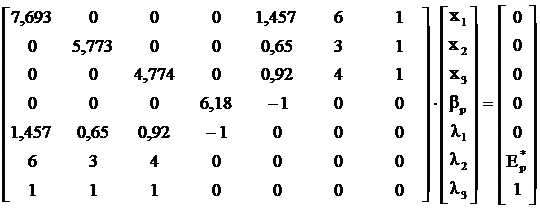
W X K

Matricea inversa W^-1 are urmatoarele valori:

Cu ajutorul matricei inverse (W^-1) putem obtine usor sistemul de ecuatii parametrice pentru determinarea frontierei eficciente si a riscului sistematic al acesteia:

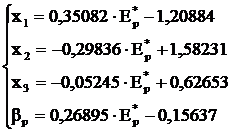
Pentru aceleasi valori dorite ale sperantei E_p^* ca si-n exemplul anterior vom obtine urmatoarea compozitie a portofoliilor eficiente corespunzatoare (si care conduc in modelul diagonal la risc minim, a se vedea tabelul 11.3).

Cu cat numarul titlurilor din portofoliu creste cu atat estimarile modelului diagonal se apropie de cele corecte.

O alta sursa a aproximarii o constituie reprezentativitatea portofoliului de piata pentru titlurile analizate. Daca acest portofoliu nu reprezinta un substitut perfect in care (), atunci estimarile in modelul diagonal vor fi afectate corespunzator erorii de reprezentare a pietei financiare.

3. EVALUAREA ACTIVELOR FINANCIARE CU AJUTORUL MODELULUI A.P.T.

3.1.COMPONENTELE RENTABILITATII ACTIVELOR FINANCIARE

Rentabilitatea scontata a oricarui proiect de investitii, pe piata finaciara, trebuie sa cuprinda:

a. o rentabilitate minim realizabila la nivelul economiei nationale (dobanda la CEC sau la viitoarele obligatiuni de stat). Este rentabilitatea minima pentru active fara, pentru cele mai sigure plasamente pe piata financiara privind plata dobanzii si rambursarea capitalului plasat.

b. o prima de risc sistematic corespunzatoare incertitudinii (variabilitatii rezult.) proiectului de investitii respectiv. Riscul specific nu va fi remunerat de piata financiara deoarece el poate fi eliminat prin diversificare.

Dobanda la titlurile de stat reprezinta o buna evaluare a randamentului minim acceptabil pe piata financiara respectiva. Este deci rentabilitatea activului fara risc notata cu R_f. Fiind o dobanda fara risc, se considera o dobanda certa( a unui activ cert). Investitorii, cu aversiune fata de risc, pot cumpara aceste titluri in schimbul unei dobanzi minime. De asemenea, investitorii, cu preferinta pentru risc, pot sa se imprumute la aceasta dobanda fara risc pentru a cumpara si detine apoi active riscante, dar cu rentabilitate superioara.

Ceea ce intereseaza este rentabilitatea scontata in viitor de la portofoliul de piata ( E (R_M)). Diferenta intre E(R_M) si rentabilitatea minim acceptabila (R_f) , reprezinta pretul riscului sistematic pentru orice activ riscant.

Pret risc sistematic = E (R_M) - R_f

La formarea acestui pret al riscului de piata contribuie fiecare activ riscant .

Contributia marginala a activelor riscante la formarea riscurilor sistematic se masoara prin coeficientul de volatilitate b al fiecarui titlu. Fiind un parametru exogen al modelului CAPM, este considerat (relativ) constant in timp.

Prima de risc sitematic asociata unui activ riscant este, deci, determinata de pretul riscului sistematic (acelasi pentru toate activele riscante) si coeficientul b specific fiecarui activ riscant :

Prima de risc sistematic = (E (R_M) - R_f) b_i

unde I= titlul riscant care se evalueaza

Astfel rentabilitatea scontata a unui activ riscant (R_i) este formata din :

- rentabilitatea activului fara risc R_f si

- prima de risc sistematic (E (R_M) - R_f) b_i

R_i = R_j + (E (R_M) - R_f) b_i

Factorii de determinare a rentabilitatii individuale a unui titlu, dupa CAPM sunt :

rentabilitatea activelor fara risc R_f

pretul riscului sistematic (E (R_M) - R_f) b_i

coeficientul de volatilitate b_i

In spiritul rationalismului critic, multi cercetatori s-au intrecut in a arata ca modelul CAPM este prea simplificator pentru realitatea economico-financiara. Dupa ei rentabilitatea si riscul unui titlu financiar nu pot fi intro relatie liniara de o singura variabila, respectiv rentabilitatea si riscul portofoliului de piata. Alte critici s-au concentrat asupra presupusei stabilitati in timp a coeficientului b (si el o variabila aleatoare ca si cursurile bursiere) sau asupra valabilitatii modelului pe o singura perioada (uniperiodic), in timp ce plasamentele financiare sunt multiperiodice. Drept replica la aceste critici s-au elaborat CAPM - multiperiodic sau CAPM - Consum (Merton, 1973; Breeden, 1979).

In baza preocuparilor de eliminare a ipotezelor prea restrictive ale CAPM, cercetatorul american S. Ross a elaborat un model mult mai general, intitulat modelul de evaluare prin arbitraj (APT=Arbitraje Pricing Theory, in engleza).

Pentru o piata concurentiala, multimea de arbitraje pret-valoare va face ca valoarea activelor sa genereze aceeasi rentabilitaet la un risc anume asumat. Aceasta rentabilitate va fi in functie de rentabilitatea sperata a activului (E(R_i)), precum si in functie de mai multi factori macroeconomici (F_n), cu coeficienti (b_in) mai mult sau mai putin sensibili:

in care

= rentabilitatea aleatoare a activului i.

= speranta de rentabilitate a activului i.

b_in = coeficientul de sensibilitate a rentabilitatii R_I, in raport cu factorul F_n.

= valoarea factorului 'n' a carui medie este nula si dispersie finita (factorii sunt ortogonali intre ei).

e_i = valoare reziduala de medie nula ce masoara rentabilitatea neanticipata prin factorii F_n (riscul specific).

Cu alte cuvinte orice rentabilitate observata () nu poate fi explicata decat, intr-o anumita masura, prin rentabilitatea anticipata (sperata =). Partea de rentabilitate, observata si neanticipata (ex ante), se datoreaya, in acelasi timp, unor factori explicativi comuni sau sistematici (F_n) si unor variabile specifice fiecarui activ (e_i). Modelul APT considera deci rentabilitatea unui activ ca fiind functie liniara de 'n' factori comuni si de variabilele specifice. Toate aceste variabile sunt independente intre ele de medie nula si de dispersie finita.

3.2. FUNDAMENTAREA MODELULUI A.P.T.

Se porneste de la relatiile cunoscute ale rentabilitatii observate si sperate a titlului 'i'.

Dintre aceste doua ecuatii ale modelului de piata si ale CAPM, ale rentabilitatii observate () si ale celei sperate () se poate usor calcula partea anticipata si cea neanticipata (ce tine de factorul sistematic+portofoliu de piata si de factorul specific e_i

Se constata deci ca F₁ reprezinta factorul 'portofoliu de piata' de medie nula, ca toti ceilalti factori F_n ai modelului de arbitraj, APT.

In practica, orice investitor poate constitui un portofoliu atat de bine diversificat incat sa elimine riscul specific(e_i). Singurul care va fi remunerat este riscul sistematic datorat coeficientilor de sensibilitate ai factorilor comuni 'b_in'. Toate portofoliile eficiente se vor gasi nu pe frontiera eficienta (CML), ca in cazul Capm, ci intr-un 'plan eficient', in cazul a doi factori comuni, intr-un spatiu eficient, in cazul a trei factori s.a.m.d. In raport cu acesti factori se poate stabili o relatie de liniaritate pentru speranta de rentabilitate (

in care sunt constante.

Toate portofoliile sau activele individuale, a caror rentabilitate depinde de coeficientii de sensibilitate b_in, trebuie sa se gaseasca pe acelasi 'plan eficient' si sa prezinte o rentabilitate sperata, conforma relatiei de mai sus. Daca nu va fi asa, vor avea loc operatiuni de arbitraj (de castig obtinut fara investitie suplimentara si fara risc) pana cand echilibrul se va restabili.

Daca se obtine atunci:

in care

rentabilitatea sperata a unui portofliu,a vand o sensibilitate egala cu 1 la factorul F_n si nula pentru toate celelalte

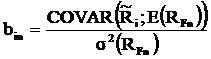
Se observa usor similitudinea cu CAPM, dar, mai ales, generaliyarea pe care modelul APT o face legand rentabilitatea sperata a unui activ de mai multi factori macro-economici de risc. Cu toate aceste avantaje, modelul ATP nu ne poate spune (1) cati factori comuni de risc sunt si (2) nici care sunt acesti factori. Modelul spune simplu ca pot fi n factori comuni, un numar mult inferior numarului de active din economie. O mare dificultate este, de asemenea, de a determina rentabilitatea sperata datorata fiecarui factor F_n.

Aceste inconveniente, adesea insurmontabile, fac astazi CAPM sa fie modelul de evaluare cel mai utilizat si nu modelul APT. datorita cercetarilor lui Chen, Roll si Ross (1983) au putut fi identificati patru factori comuni independenti in economia SUA:

1)     - schimbari neanticipate ale ratei inflatiei;

2)     - primele de risc, ca diferenta intre dobanzile la cadenta ale obligatiunilor de stat si ale celor private;

3)     - panta ratelor de dobanda pe termen lung, in raport cu cele pe termen scurt;

4)     - rata de crestere a productieie industriale.

Identificarea acestor factori se face prin utilizarea metodelor de analiza factoriala sau de analiza a compozantei principale.

3.3 APLICATIE LA MODELUL APT

Reluam exemplul celor trei titluri de la modelul diagonal ale caror rentabilitati sunt acum determinate de rata rentabilitatii fara risc () si de doi factori macro-economici F₁ si F₂ explicativi ai primei de risc :

Din tabel se poate verifica usor conditia de ortogonalitate a vectorilor valorilor posibile ale celor doi factori macroeconomici, F₁ si F₂:

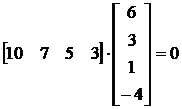
Pornind de la datele de previziune de mai sus, se poate stabili daca rentabilitatea sperata a celor trei titluri respecta echilibrul cerut prin modelul APT sau daca aceasta este supra sau subevaluata.

Preturile unitare (l₁ si l₂) ale riscului sistematic determinat de cei doi factori macro-economici sunt urmatoarele:

Coeficientii de volatilitate (b_in) ai celor trei titluri in raport cu fiecare factor macro-economic se pot determina prin utilizarea retelei de calcul evocate anterior (a se vedea tabelul urmator).

In cadrul normativ al modelului APT, sperantele de rentabilitate ale celor trei titluri vor fi urmatoarele:

E(R₁)=3+3,1*1,7629-1,2*1,2752=6,93475

E(R₂)=3+3,1*0,3343-1,2*0,033557=4,0323

E(R₃)=3+3,1*0,4863-1,2*0,4698=3,94377

Comparand acum aceste sperante de rentabilitate (dupa modelul APT) cu previziunile operatorilor financiari (din datele initiale ale aplicatiei) rezulta ca doar evaluarea titlului 3 este facuta la echilibrul proceselor de arbitraj:

E(R₃)_initiala = 4% = 3,94377 = E(R₃)_APT

Titlurile 1 si 2 sunt subevaluate (6<6,93475 si 3<4,0323). Constienti acum de 'pretul lor mic' (la echilibrul proceselor de arbitraj) operatorii financiari vor constitui portofolii de arbitraj, cumparand titlurile 1 si 2 (mai ieftine). In urma acestor operatii, preturile celor doua titluri vor ceste pana la 'pretul lor unic' de echilibru.