Curba lui phillips

Informatii » afaceri » economie

asiguraricomertcontabilitatedrepteconomielegislatiestatisticatransporturiturism

CURBA LUI PHILLIPS

Teoria moderna a inflatiei a fost influentata intr-o masura deosebita de aparitia modelului curbei lui Phillips[1], iar mai tarziu de criticile aduse acestei curbe. Pe parcursul existentei aceste curbe se pot distinge trei etape importante:

a)formarea notiunii de catre Phillips si Lipsey[2], care a avut ca punct de pornire presupunerea ca intre rata somajului exista o relatie stabila, invers proportionala;

b)diferenta dintre curba lui Phillips pe termen scurt si cea pe termen lung (diferenta este demonstrata de catre Milton Friedman si E.Phelps prin teoria "ratei naturale a somajului");

c)critica adusa curbei lui Phillips de catre adeptii scolii asteptarilor rationale, care considerau ca nu exista nici o forma sistematica de compunere intre inflatie si somaj.

1 CURBA INITIALA A LUI PHILLIPS

In 1952, A.W.Phillips a revolutionat teoria moderna a inflatiei printr-un articol, consacrat relatiei dintre variatia salariilor si rata somajului. Aceasta relatie a fost dedusa din analiza celor doua variabile (somajul si salariile) pe o perioada de peste 50 de ani, mai precis intre anii 1861-1913, in Marea Britanie.

Phillips, pe baza relatiei de mai sus (care este de forma neliniara, negativa), a dedus ca aceasta se potriveste perfect urmatorului interval de timp, adica perioadei 1913-1957. Conform functiei, rata de crestere a salariilor scade pe masura ce creste rata somajului.

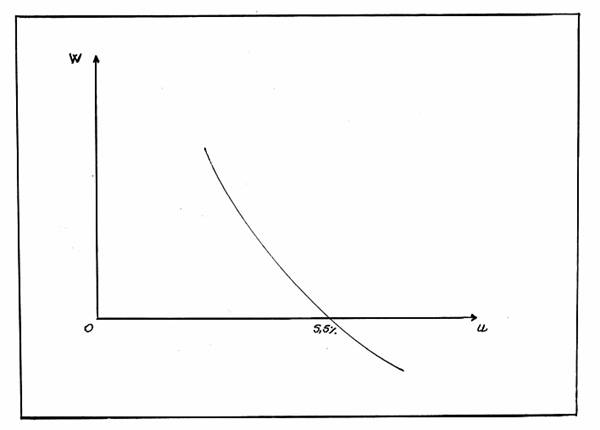
Figura nr.5. Curba initiala a lui Phillips

Unde: U=rata somajului (in procente)

W[3]=rata de variatie a salariilor (in procente)

Curba de mai sus  ne releva doua aspecte foarte importante:

a)cand rata somajului este de 5,5% salariile stationeaza (W=0)

b)Phillips a dedus de asemenea ca atunci cand rata somajului scade salariile cresc mai repede, iar atunci cand rata somajului are tendinta de crestere, salariile cresc mai lent.

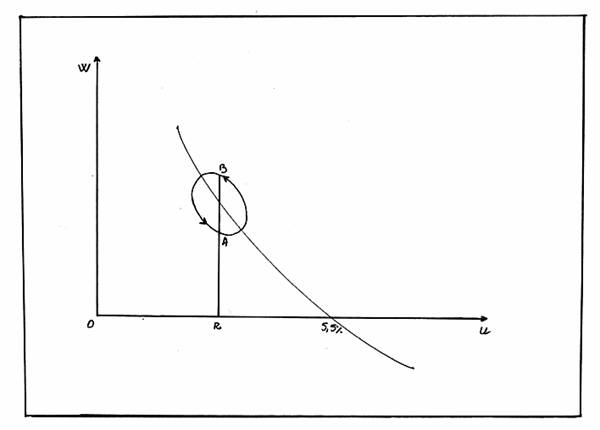
Figura nr.6. Curba lui Phillips

Pe parcursul cercetarilor sale, Phillips nu a urmarit ca relatia mai sus mentionata (dntre rata somajului si rata de crestere a salariilor), sa fie negativa, ci mai degraba el a fost atras de gasirea unei relatii care sa fie stabila.

In figura nr.6 se poate observa ca unei valori a ratei somajului (notata cu u), ii corespunde doua valori ale ratei de variatie a salariilor (w). Ratei somajului ii corespunde doua puncte care reprezinta, pe de o parte, rata inflatiei prin salarii reprezentata de RB care se datoreaza scaderii ratei somajului (cand cererea de forta de munca are un ritm ascendent), iar pe de alta parte, rata inflatiei prin salarii RX care apare cand rata somajului creste (cererea de forta de munca in acest caz se reduce).

Rezulta ca rata de crestere a salariilor nu depinde numai de rata somajului, de nivelul excesului de cerere, dar si de variatia acestui nivel. Phillips spunea in 1958 ca "la orice nivel al somajului exista o tendinta clara a ritmului de variatie a ratei salariilor de a se situa deasupra nivelului mediu, atunci cand somajul descreste in perioada de avant economic, si sub nivelul mediu, cand somajul creste in perioada de declin a ciclului economic".

Curba lui A.Phillips a fost construita pe baza unor date reale (situatia din Marea Britanie de la inceputul secolului nostru si sfarsitul secolului trecut) si a constituit un model ce incerca sa explice ceea ce nu reusise teoria economica, si anume: de ce nivelul salariilor are tendinta continua de crestere.

Cel care a incercat sa teoretizeze acest model empiric a fost R.G.Lipsey.

2 MODELUL LUI R.G.LIPSEY

Lipsey porneste in alcatuirea modelului sau de la curba originala a lui Phillips, dar si cu ipoteza unei piete, unice a fortei de munca (adica sistemul unei cereri si oferte pe o piata unica). Lipsey, in modelul sau ignora faptul ca fiecare piata de munca, (fie ea la nivel national, regional sau la nivel de ramura economica) are propriile sale caracteristici. Totodata, Lipsey a utilizat in modelul sau salariul nominal, spre deosebire de teoria economica care considera ca cererea si oferta de pe piata muncii sunt functii ale salariului real.

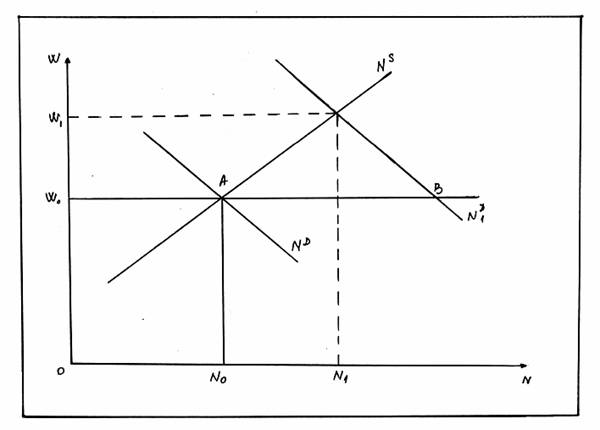
Figura nr.7. Modelul lui R.G.Lipsey

N^D=cererea de forta de munca

N^S=oferta de forta de munca

In figura nr.7 se poate observa ca cererea de forta de munca (notata cu N^D) si respectiv oferta de forta de munca (N^S) reprezinta functii liniare ale salariului nominal. Piata fortei de munca se afla echilibru atunci cand N^D si N^S inregistreaza aceiasi valoare (punctul A). Atunci cand diferenta dintre N^D si N^S este zero, rata de variatie a salariilor nominale este considerata nula.

Pe piata, oferta de forta de munca este alcatuita din numarul persoanelor angajate si numarul celor fara loc de munca:

N^D=N+U, unde:

N=numarul celor angajati;

U=numarul somerilor.

Numarul de salariati plus numarul locurilor de munca vacante alcatuiesc cererea de forta de munca.

N^S=N+V, unde:

V=numarul locurilor de munca vacante.

Excesul de cerere de forta de munca este reprezentat de diferenta dintre numarul posturilor vacante si numarul somerilor.

X=N^S-N^D, unde:

X=excesul de cerere de forta de munca.

X=N+V-N-U=V-U

In ipoteza ca forta de munca va deveni mai numeroasa (vezi figura nr.7), de exemplu de la N^D la N₁^D), un motiv constituind-l faptul ca se asteapta o crestere a veniturilor, atunci excesul de cerere de munca, reprezentat de segmentul AB, apare pentru nivelul curent al salariului nominal (W₀). In practica macroeconomica nivelul salariilor creste (de la W₀ la W₁) odata cu cresterea gradului de ocupare a fortei de munca. Lipsey a extrapolat curba lui Phillips asupra pietei fortei de munca cu ajutorul a doua functii:

a)     functia de ajustare a salariilor (care reprezinta o relatie intre excesul de cerere de forta de munca si variatia salariilor nominale);

b)     functia X-U, care este o relatie negativa intre excesul de cerere de forta de munca si rata somajului.

2.1 FUNCTIA DE AJUSTARE A SALARIILOR

Functia de ajustare a salariilor arata ca rata de variatie a nivelului salariilor este determinata de diferenta dintre cerere si oferta, cu alte cuvinte de excesul de cerere de forta de munca:

X=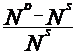, unde:

X=excesul de cerere de forta de munca

N^D=cererea planificata de forta de munca

N^S=oferta planificata de forta de munca.

Cu cat cererea depaseste mai mult oferta, cu atat nivelul salariilor va creste mai repede. Daca insa exista un raport de egalitate intre cererea de forta de munca si oferta de forta de munca, nivelul salariului nominal va ramane constant.

	O

 

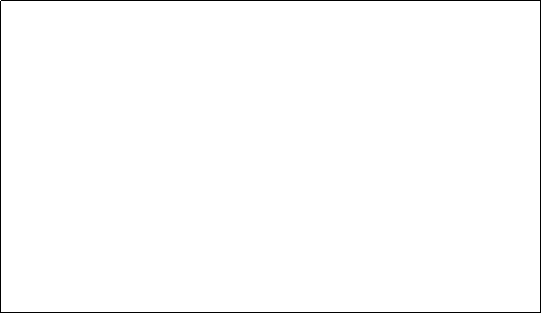
Astfel, functia de ajustare a salariilor este:

W=

W=k^.,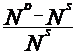

sau altfel spus variatia nivelului salariilor nominale este direct proportionala cu excesul de cerere de forta de munca.

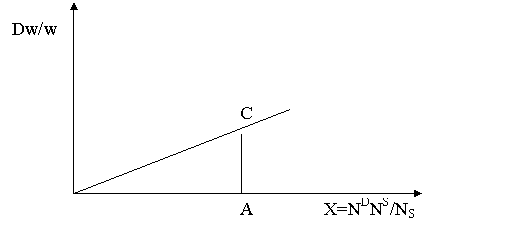
In figura nr.8, un exces de cerere de forta de munca produce o variatie relativa AC a salariilor nominale. In vreme ce nivelul salariilor si variatia acestuia sunt observabile pe cale empirica, excesul de cerere de forta de munca N^D-N^S reprezinta o diferenta intre doua marimi planificate, care nu pot fi observate statistic, in mod direct. Pentru a aproxima excesul de cerere de forta de munca a fost necesara introducerea unei relatii ajutatoare, pe care R.G.Lipsey a obtinut-o facand legatura intre excesul de cerere de forta de munca si rata somajului.

2.2 FUNCTIA X-U

Alaturi de functia de ajustare a salariilor, Lipsey a stabilit si o relatie negativa intre excesul de cerere de forta de munca(X) si rata somajului (u).

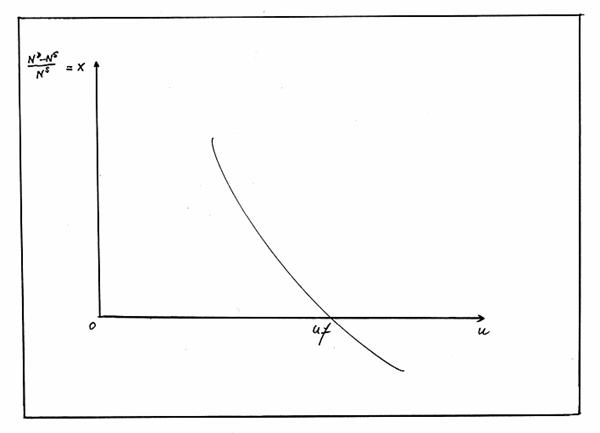
Figura nr.9. Functia X-U

Uf=nivel functional al somajului

In conceptia lui Lipsey lipsa excesului de cerere presupune un numar al somerilor egal cu cel al locurilor de munca vacante si, astfel curba x-u intersecteaza axa OU(abscisa din figura nr.9) intr-un punct Uf, care este echivalent cu un exces al cererii egal cu zero (nul). Daca cunoastem acest punct (este vorba de Uf), Lipsey era de parere ca o crestere a excesului de cerere de forta de munca va genera o scadere a somajului (u) si ca o crestere a excesului de oferta de forta de munca va conduce la majorarea ratei somajului.

Din combinarea celor doua functii (functia de ajustare a salariilor si relatia x-u), rezulta o curba specifica a lui Phillips, care se refera la o piata individuala a fortei de munca. Conform modelului Phillips-Lipsey, rata inflatiei prin salarii se explica prin excesul de cerere de pe piata fortei de munca.

3 CURBA LUI PHILLIPS IN TIMP

Milton Friedman si Phelps sunt primii economisti care au manifestat neincredere la adresa curbei lui Phillips. Ei si-au pus intrebarea daca aceasta curba reprezinta o relatie stabila atat pe termen lung dar si pe termen scurt. Totodata Friedman critica interpretarea data de Lipsey curbei lui Phillips, in special datorita faptului ca Lipsey nu a luat in calcul asteptarile inflationiste. Phelps si Fiedman aratau ca orice punct luat de pe curba lui Phillips determina o anumita rata de inflatie, dar daca rata anticipata a inflatiei se va schimba, acest lucru va conduce la modificarea curbei lui Phillips. Orice rata a inflatiei actuale, mai ridicata, va determina peste o perioada relativ lunga de timp, o rata mult mai ridicata a inflatiei asteptate si in acest mod curba lui Phillips va avea o tendinta de urcare ce va impiedica orice compensare intre inflatie si somaj pe termen lung (vezi figura nr.11).

In contextul celor afirmate mai sus Phelps declara: "daca se astepta o crestere generala a preturilor de 4% pe an, de ce ar fi rata asociata somajului mai scazuta sau mai ridicata decat cea care ar exista daca s-ar astepta o stabilitate a preturilor viitoare, iar cererea globala s-ar comporta de o maniera care sa determine preturi medii stabile?". Desi nu neaga existenta unei curbe pe termen scurt Friedman si Phelps sustin ca acesta se modifica odata ce se schimba rata anticipata a inflatiei.

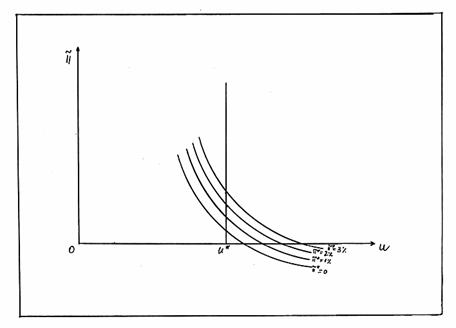
Figura nr.10. Curba lui Phillips in timp

In figura de mai sus se evidentiaza mai multe curbe ale lui Phillips, singura diferenta dintre ele constand in faptul ca fiecare este trasata pe baza unei rate a inflatiei anticipate diferite (respectiv pentru 0%, 1%, 2% si 3%). Conform opiniei celor doi economisti (Friedman si Phelps) tocmai din acest motiv ecuatia ce da curba lui Phillips trebuie sa arate astfel:

r=f(u)+r^*, unde:

r=rata inflatiei

u=rata somajului

r^*=rata anticipata a somajului

Din datele de mai sus se pot extrage urmatoarele concluzii:

-curba lui Phillips se modifica de fiecare data, odata cu rata anticipata a inflatiei;

-orice schimbare a ratei anticipate a inflatiei are drept urmare deplasarea curbei lui Phillips ascendent (daca rata inflatiei asteptate creste) si descendent (daca rata inflatiei anticipate inregistreaza o scadere).

4 INOVATIILE ADUSE DE SAMUELSON SI SOLOW CURBEI LUI PHILLIPS

P.Samuelson[4] si R.Solow[5] au publicat in 1960 o lucrare care a adus curbei lui Phillips o imensa popularizare. Acesti doi autori au incercat in primul rand sa demonstreze importanta conceptului teoretic de curba a lui Phillips pentru politica economica a unei tari. Specificul tratarii curbei lui Phillips de catre Samuelson si Solow deriva din urmatoarele motive:

a)curba initiala a lui Phillips (care reprezinta o relatie intre rata somajului si rata de variatie a salariilor) a fost modificata, astfel incat, ea a devenit o relatie intre rata somajului si rata inflatiei.

b)Samuelson si Solow au transformat conceptul teoretic intr-un instrument de politica economica care permitea realizarea de programe guvernamentale ce puteau combina, alternativ, rate ale somajului cu rate ale inflatiei.

Dupa aparitia lucrarii celor doi specialisti, aceasta formulare a curbei lui Phillips (ca relatie intre inflatie si rata somajului) a ajuns sa aibe prioritate in dezbaterile ce aveau aceasta tema, ca si in cercetarile ulterioare. Exista insa o relatie intre formularile lui Phillips-Lipsey si ale lui Samuelson-Solow privind curba lui Phillips, care este data de o formula a marjei de profit inclusa in pret. Agentii economici isi determina preturile de vanzare ale produselor lor cu ajutorul unui adaos fix, calculat de baza costurilor efective pe unitatea de munca depusa (acest adaos include marfa de profit obisnuita la nivel de ramura precum si un coeficient care sa remunereze deprecierea capitalului fix):

P=(1+a), unde:

P=pretul produsului (sau nivelul pretului)

W=nivelul salariului nominal;

N=numar de salariati;

X=nivelul productiei efective

=costul pe unitatea de munca

a=adaos

Dupa logaritmare si derivare rezulta:

log P=log (1+a)+log W-log A

sau , unde:

r=rata inflatiei

W=rata de crestere a salariilor nominale

=rata de crestere a productivitatii muncii

Din modul de formare a pretului se deduce ca rata inflatiei este egala cu diferenta dintre rata de crestere a salariilor nominale si rata de crestere a productivitatii muncii.

In continuarea demonstratiei lor, Samuelson si Solow, presupun ca, curba lui Phillips se mai poate scrie sub urmatoarea forma:

W=r^*+bu^-1+, b>0

01, unde:

r^*=rata anticipata a inflatiei.

Rata de variatie a salariilor nominale W (exprimata in procente) depinde de rata asteptata a inflatiei (r^*), de gradul de presiune al cererii (notat cu u^-1) si de rata de crestere a productivitatii muncii ().

Din penultimele doua relatii se obtine curba lui Phillips, modificata de Samuelson si Solow:

r=r^*+bu^-1-(1-)

Aceasta ultima formula ne permite sa concluzionam ca rata inflatiei(r) este determinata de presiunea exercitata de cerere asupra pietei muncii (bu^-1), de rata asteptata a inflatiei(r^*) si de termenul (1-), care arata partea din crestere a productivitatii muncii ce nu se transfera asupra muncitorilor sub forma unor cresteri salariale. Cu cat aceasta componenta a productivitatii muncii este mai ridicata, cu atat este mai scazuta rata inflatiei.

In acelasi timp, Samuelson si Solow, au dorit transformarea curbei lui Phillips dintr-o teorie economica, intr-un instrument de politica economica. Astfel, in opinia lor, fiecare punct de pe curba lui Phillips putea fi interpretat ca o varianta posibila a politicii economice dusa de guvern.

Intre punctele A si B (vezi figura nr.11) de pe curba R a lui Phillips se manifesta o relatie invers proportionala intre ratele somajului si ale inflatiei. Cu alte cuvinte se poate obtine o inflatie mai scazuta in schimbul unui somaj mai ridicat, sau se poate realiza un somaj mai scazut, dar in acest caz inflatia va cunoaste un trend ascendent.

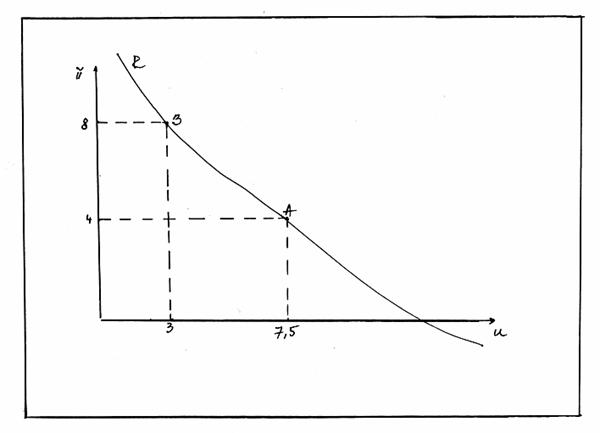
Figura nr.11. Curba lui Phillips

Spre exemplu, plecam de la ipoteza ca o perioada relativ indelungata de timp preturile au crescut cu 4% anual si ca rata somajului s-a mentinut in jur de 7,5%. Guvernul considerand ca aceasta rata a somajului este ridicata incearca sa o reduca prin stimularea cererii, cum ar fi, de exemplu, cresterea deficitului bugetar finantat printr-o crestere a ofertei de bani. Modelul macroeconomic este al ocuparii, care are atat efecte reale, cat si efecte inflationiste, astfel incat cresterea cererii globale nu numai ca reduce rata somajului dar si sporeste rata inflatiei.