|
|
|
PROIECT DE TEHNOLOGIE DIDACTICA
Clasa: a VII-a A
Obiectul: Matematica optionala
Unitatea de invatare: Geometria triunghiului: Relatii metrice
Tema lectiei: "Aplicatii si completari la teorema lui Pitagora"
Tipul lectiei: Lectie de fixare si consolidare a cunostintelor.
Scopul lectiei: Dezvoltarea la elevi a priceperilor si deprinderilor de rezolvarea problemelor cu continut practic.
Obiective operationale: La sfarsitul orei elevii sa stie:
O1 - sa efectueze calcule cu numere reale utilizand proprietatile operatiilor si formule de calcul prescurtat
O2 - sa utilizeze proprietati calitative si metrice ale figurilor geometrice in rezolvarea unor probleme
O3 - sa construiasca probleme , pornind de la un model
O4 - sa identifice si sa diferentieze etapele unui rationament matematic, prezentat in diverse forme
O5 - Sa manifeste interes pentru folosirea tehnologiilorinformatiei in studiul matematicii
Material didactic: planse, manual, culegere, calculator personal
Fiind o ora de matematica optionala la clasa a VII-a s-a recurs la folosirea unor programe de calculator pentru formarea deprindelor de calcul la aplicarea teoremei lui Pitagora imbinat cu date istorice remarcabile despre viata si activitatea lui Pitagora si despre scoala intemeiata de acesta.
Material bibliografic folosit:
1. Ioan Dancila: Matematica gimnaziului intre profesor si elev, Ed. Aramis, 2001
2. V. Bobancu: Caleidoscop matematic, Ed. Albatros,1979
3. Eugen Guran: Matematica recreativa, Ed. Junimea, 1985
4. Ioan Dancila : Matematica aplicata, Ed. Sigma 2000
5. Surse de internet: http://www-gap.dcs.st-and.ac.uk/~history/Timelines/index.html; www.referatele.com
6. MATE 2000+3, culegere de probleme pentru clasa a VII-a
Evenimenteleinstrutirii
Activitati ale lectiei pentru indeplinirea functiilor
Metode
Stimularea reactualizarii cunostiintelor
Intensificarea retinerii si asigurarea transferului
I. Exercitii de antrenament mintal:
Recapitularea cunostintelor referitoare la "Relatii metrice"
1. Triunghiul dreptunghic
2. Teorema catetei
3. Teorema inaltimii
4. Teorema lui Pitagora
Verificarea temei pentru acasa: demonstreaza relatia lui Carnot
1. Se verifica daca au studiat ambele cazuri: M in interiorul triunghilui ABC si M in exteriorul triunghiului.
2. Triunghiurile considerate
3. Relatia rezulta imediat din aplicarea teoremei lui Pitagora si insumtnd termenii obtinuti
Elevii care au avut de pregatit documentare suplimentara prezinta date despre:
Viata si activitatea lui Pitagora
Scoala lui Pitagora
Contributii in geometrie
Contributii in aritmetica
Demonstratii ale faimoasei teoreme
Aplicatii in probleme
Curiozitati
II. Recurgerea la o situatie problema
1.
Sa se demonstreze ca numerele de forma 
;
z = m si 
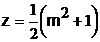formeaza triplete pitagoreice,
adica x2+y2 = z2.
2. Demonstratii interesannte "fara cuvinte" bazate pe figuri echivalente, folosind ca unghiurile ascutite intr+un triunghi dreptunghic sunt complementare.
Schitele sunt prezentate in Anexa
3. Folosind modelul e demonstratie a teoremei lui Pitagora dat de Bhaskara sa se construiasca un patrat echivalent cu un dreptunghi cu latimea 1 si lungimea 5.
Conversatia
Problematizare
Conversatia
Problematizare
Activitatea independenta
Clasa este impartita in 2 grupe de elevi, si cate un responsabil care supravegheaza modul cum opereaza la calculator.
Fiecare elev va face cate o aplicatie la calculator pentru verifcarea modului cum aplica teorema lui Pitagora si evaluarea corectitudinii calculelor.
Elevii care inca au dificultati in rezolvare problemelor vor fi ajutati de catre responsabili.
(se foloseste un program care pune elevul in situatia de a aplica teorema pentru cazuri simple: intr-un triunghi dreptunghic se cunosc 2 laturi sa se afle a treia latura)
Evaluarea rezultatelor
Calculatorul afiseaza numarul greselilor din setul de 10 aplicatii.
Tema pentru acasa
1. Sa se demonstreze ca numerele de forma x=k(p2-q2), y = 2kpq si z = k(p2-q2) pot fi lungimile laturilor unui triunghi dreptunghic.
2. Demonstraza ca intr-un paralelogram suma patratelor lungimilor laturilor este egala cu suma patratelor lungimilor diagonalelor
ANEXE
Anexa 1
Pythagora din Samos
aproxim. 569 (584) i.Hr. in Samos, Ionia - aprox. 475 (497) i.Hr. in Metapont
Pitagora, matematician si filozof grec, a studiat cu Anaximandru, a calatorit si s-a instruit in Egipt si Chaldeea, s-a stabilit in Cretona unde a infiintat o scoala filozofica ce reunea peste 300 de pitagorieni, unde a instituit o disiplina severa de viata si de munca, emblema lor era pentagonul stelat. Din studiul numerelor, pitagorienii au conceput numerele figurative, numerele perfecte, numerele amiabile, au definit numere pare si impare, au studiat media aritmetica, geometrica si armonica, au descoperit irationalitatea - utilizand teorema ce-i poarta numele, cunosteau cele cinci poliedre regulate, tabla inmultirii, sistemul zecimal
In astronomie, ideea ca Pamantul se invarte in jurul unui "foc central" apare pentru prima data in cadrul scolii pitagoriene. Pitagora nu a lasat nimic scris, de aceea este greu de delimitat conceptiile si contributiile stiintifice si filozofice de ale discipolilor sai, mai ales ca prima descriere a operei si a scolii sale a fost intocmita cu 13 decenii mai tarziu.
Cu toate ca poate ar fi fost mai corect ca alaturi de teorema catetei, si a inaltimii sa se numeasca eventual teorema ipotenuzei, Pitagora a ramas cunoscut in mod special datorita teoremei sale, desi a fost descoperita cu mult inaintea lui Pitagora si se presupune ca doar a extins-o la triunghiuri dreptunghice ale caror laturi sunt exprimate prin orice numar pozitiv (initial erau numai numere naturale).
Se spune ca pitagorienii au interzis divulgarea
marii teoreme, deoarece intr-un patrat ducea la relatia 
,
o adevarata erezie pentru cei ce nu acceptau decat numere
rationale pentru descrierea fenomenelor naturii, deci si a
geometriei.
Vechii constructori egipteni foloseau pentru constructia unghiului drept o funie cu 12 noduri echidistante, legata sub forma de inel si fixata cu 3 tarusi si obtineau un triunghi dreptunghic cu laturile de (3; 4; 5), utilizand astfel reciproca teoremei lui Pitagora.
De altfel, teorema aceasta face parte din categoria teoremelor la care s-au inregistrat in decursul timpului recordul demonstratiilor (se presupune intre 350 - 500 de demonstratii).
"La inceput a fost numarul"
Anexa 2
Curiozitati - Pitagora
A descoperit tabla inmultirii, a studiat numerele pare si numerele impare, numerele prime si numerele compuse, numerele prime denumind numere liniare (o dimensiune), numerele compuse care se scriau ca produs de doi factori numere plane, iar numerele compuse din trei factori spatiale.
Numere triunghiulare
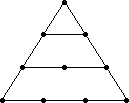
Numere patratice
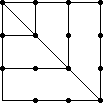1 + 3 + 5
+ + (2n-1) = n2.
Numere pentagonale
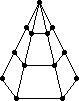
Numere prietene sau amiabile au foat numite acele numere la care suma divizorilor unui numar este egala cu suma divizorilor celuilalt numar. Pitagorienii au gasit perechea 220 si 284.
Cu ajutorul calculatorului electronic intr-o universitate din S.U.A. au fost cercetate toate numerele pana la milion. In rezultat s-a obtinut 42 de perechi de numere prietene: (220;284) (1184;1210) (2620;2924) (5020; 5564) (6232;6368) Exista si perechi de numere prietene impare: cum ar fi (12285; 14 595), (67095;87633).
Magia numerelor I-a fascinat pe adeptii lui Pitagora. Ei au considerat ca efectuarea calculelor este un lucru nedemn, insemnand indeletniciri zilnice ale oamenilor de rand, in schimb s+au ocupat foarte mult de proprietatile numerelor. Considerau ca numerele impare sunt nemuritoare, deoarece nu se impart la 2, numarul 7 este numar medical si este decisiv pentru bolnavii contagiosi si cei operati; ca 8 (octava) semnifica dragostea, prietenia, chibzuinta, gandirea. Universul este analogat cu numarul 10, iar 10 reprezinta perfectiunea. Pentru a demonstra ca 10 este perfectiunea si ca exprima universul, Pythagoras avea sa adauge celor noua cercuri (planete cunoscute atunci) (cer, Soarele, Luna, Pamant, Mercur, Venus, Martie, Jupiter si Saturn) cel al zecelea - al Anti-Pamantului (o inventie arbitrara). Deasemenea cunosteau ca Pamantul are forma sferica.
O semnificatie aparte a avut numarul 36. El i-a impresionat pe pythagorieni foarte mult datorita proprietatilor sale. Pe de o parte, el reprezinta suma cuburilor primelor trei numere (13+23+33), pe de alta - este suma primelor patru numere pare si impare:
(2+4+6+8) + (1+3+5+7) = 36.
De aceea au considerat ca juramantul cu numarul 36 este cel mai crunt. Acest "juramant" au depus si pentru a nu divulga secretul teoremei lui Pitagora. Iar legenda spune mai departe ca un adept al lui Pitagora care a divulgat teorema, celor neinitiati s-a pierdut in urma unui naufragiu, suportand razbunarea zeilor.
Anexa 3
Demonstratii ale teormei lui Pitagora:
b c
c a a b
b c
Se
scrie aria patratului mare in doau feluri:
(c+b)2
= a2 + 4
.
a b c
II. Abraham Garfield (fost presedinte SUA)
- se arata ca triunghiul obtinut este dreptunghic isoscel
- se scrie
aria trapezului in doua moduri.
b a 
c
c b
III. Bhaskara (sec, XII.)
patrulaterul din interior
este patrat
aria paptratului
mare:
IV. Henry Perigal (a decupat cu foarfeca dintr-o hartie)
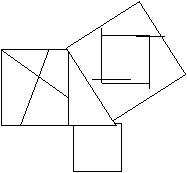
V. Bčzout (1768)
A
DDAC
DDBA DABC
Anexa 4
Folosind demonstratia data de Bashkara se efectueaza practic urmatoarea problema:
Se da un dreptunghi cu latimea de 1 cm si lungimea de 5 cm. Prin patru taieturi sa se decupeze figuri geometrice care sa acopere un patrat.
Solutie: Patratul si
dreptunghiul sunt figuri echivalente, deci patratul va avea aria 5 cm2,
de unde gasim latura patratului 
, putem construi acest numar folosind
teorema lui Pitagora intr-un triunghi dreptunghic cu catetele de 1 cm si 2
cm.
Aplicatia practica: Dreptunghiul se poate
imparti in 5 patrate. Cate 2 patrate se grupeaza
si ramane un patrat care se decupeaza. Am folosit 2
taieturi. Dreptunghiurile se taie pe diagonale si obtinem ,
care va fi latura patratului. Se
asaza figurile obtinute ca mai sus si se formeaza
patratul.
