
|
|
|
STATISTICA INFERENTIALA
Statistica descriptiva se ocupa de analiza datelor sub aspectul caracteristicilor lor intrinseci (frecventa valorilor, indicatorii tendintei centrale, ai imprastierii sau formei distributiilor). Tinta finala a metodei stiintifice insa nu se limiteaza la descrierea datelor ci vizeaza evidentierea relatiilor dintre ele si, pe aceasta baza, predictia si intelegerea fenomenelor psihice. Aceste proceduri fac parte din ceea ce se numeste statistica inferentiala
Cand masuram o anumita caracteristica a unui individ (stabilitatea emotionala, anxietate, etc.) scopul implicit este acela de a efectua comparatii. Pentru aceasta insa, simpla expresie numerica a caracteristicii respective nu este suficienta.
Modalitatea de a exprima semnificatia unei anumite valori dintr-o distributie prin raportare la parametrii distributiei (medie si abatere standard) este scorul normat z (numit si nota z sau scor z). Aceasta masoara distanta dintre o anumita valoare si media distributiei, in abateri standard:
![]()
unde X reprezinta oricare dintre valorile distributiei
Scorul z se numeste si "scor standardizat". Aceasta inseamna ca poate fi utilizat pentru a compara valori care provin din distributii diferite, indiferent de unitatea de masura a fiecareia.
Exemplu: Daca un subiect obtine un scor echivalent cu z=+0.5 la un test de memorie si un scor echivalent cu z=+0.4, la un test de inteligenta, se poate spune ca are o performanta mai buna la primul test decat la al doilea.
Proprietatile scorurilor z
1. Media unei distributii z este intotdeauna egala cu 0. Aceasta rezulta din proprietatea mediei de a se diminua corespunzator daca se extrage o constanta din fiecare valoare a unei distributii. Formula de calcul pentru z implica scaderea unei constante din fiecare valoare a distributiei. Aceasta inseamna ca si media noii distributii (z) se va reduce cu constanta respectiva. Dar aceasta constanta este insasi media distributiei originale, ceea ce inseamna ca distributia z va avea media egala cu zero, ca rezultat al diminuarii mediei cu ea insasi.
2. Abaterea standard a unei distributii z este intotdeauna 1. Acest fapt decurge prin efectul cumulat al proprietatilor abaterii standard. Prima proprietate afirma ca in cazul scaderii unei constante (in cazul scorurilor z, media) din valorile unei distributii, abaterea standard a acesteia nu se modifica. A doua proprietate afirma ca in cazul impartirii valorilor unei distributii la o constanta, noua abatere standard este rezultatul raportului dintre vechea abatere standard si constanta. Dar constanta de care vorbim este, in cazul distributiei z, chiar abaterea standard. Ca urmare, noua abatere standard este un raport dintre doua valori identice al carui rezultat, evident, este 1.
Notele z prezinta doua avantaje importante: permit compararea valorilor unei distributii, si a valorilor provenind din distributii diferite, ca urmare a faptului ca se exprima in abateri standard de la medie.
Notele z au, insa, si unele dezavantaje: se exprima prin numere mici, cu zecimale, (greu de manipulat intuitiv) si, in plus, pot lua valori negative. Aceste dezavantaje pot fi inlaturate printr-un artificiu de calcul care sa conduca la note standardizate convenabile (ce corespund anumitor nevoi specifice). Iata cateva tipuri de note standard calculate pe baza notelor z.


Deci:
Toate variantele sunt obtinute prin transformarea operata pe distributia de note z.
La nici una dintre variante nu mai avem valori negative
Zecimalele nu mai sunt semnificative
Notele standard mari indica o valori mari iar notele standard mici indica valori mici.
Asa cum am vazut rezultatelor masurarilor pot lua diverse forme, curba distributiei putand fi unimodala sau multimodala, aplatizata sau inalta, simetrica sau asimetrica. In statistica exista insa un tip special de distributie, numita "distributie normala", care nu este rezultatul unui proces real de masurare ci reprezinta un model teoretic. Conceptul de "curba normala" are cateva proprietati caracteristice:
Curbe normale
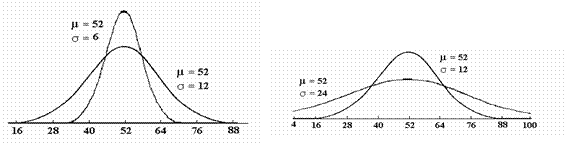
Exemple de curbe normale, care respecta conditiile de mai sus, chiar daca au medii si abateri standard diferite.
Curba normala in care valorile sunt exprimate in scoruri z se numeste curba normala standardizata. Ea are toate proprietatile enuntate mai sus, avand insa si parametrii oricarei distributii z: m=0 si s=1. Valoarea 0 pentru medie a fost aleasa conventional pentru ca astfel distributia este simetrica in jurul lui 0.
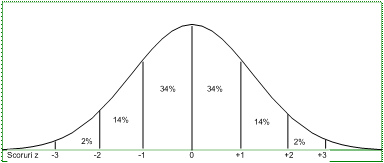
Curba normala standardizata are cateva caracteristici care sunt figurate in imaginea de mai sus si pe care este important sa le retinem:
aproximativ 34% dintre scorurile distributiei normale se afla intre medie si o abatere standard deasupra mediei (z=+1)
intre - 1z si +1z se afla aproximativ 68% dintre valorile distributiei
aproximativ 96% dintre scoruri se afla intre -2z si +2z
Curba normala are o importanta aparte pentru analiza statistica. Aceasta, deoarece se accepta faptul ca variabilele statistice s-ar distribui mai ales sub aceasta forma daca ar fi efectuate un numar mare (tinzand spre infinit) de masurari.
Procentajul ariilor de sub curba normala poate fi citit si ca probabilitatea a distributiei. Probabilitatea inseamna "frecventa relativa a aparitiei unui eveniment". Acesta se traduce prin "cat de siguri putem fi ca acel eveniment apare".
Rezulta de aici ca valorile din zona centrala a curbei sunt mai "frecvente" (mai multe), pentru ca aparitia lor este mai "probabila". In acelasi timp, valorile "mai putin probabile", apar mai rar, si se plaseaza in zonele extreme ale distributiei (curbei).
Daca probabilitatea reprezinta raportul dintre evenimentul favorabil si toate evenimentele posibile, atunci valoarea ei variaza intre 0 si 1. Ea poate fi exprimata si in procente. De exemplu, probabilitatea de 0.05 corespunde unui procentaj de aparitie de 5%
Utilizand simbolul p (de la "probabilitate"), spunem ca daca p<0.05 inseamna ca evenimentul are mai putin de 5% sanse sa apara, in conditiile unei distributii normale a curbei. De exemplu, probabilitatea de a avea un scor intre medie si z=+1 este de 0.34.
Asadar, distributia normala reprezinta un model teoretic care aproximeaza cele mai multe dintre caracteristicilor fenomenelor naturale, incluzandu-le si pe cele psihice. Cu toate acestea, distributiile reale pe care le descopera psihologii in studiile lor nu au niciodata parametrii unei curbe normale perfecte. Acest lucru este practic imposibil daca ne gandim ca o curba normala are limitele deschise, mergand spre infinit, in timp ce distributiile reale sunt finite. In ciuda acestui neajuns, aproximarea oferita de modelul teoretic al curbei normale este considerata acceptabila din punct de vedere stiintific.
Un al aspect care poate conduce la interpretari eronate este exprimarea valorilor curbei normale in scoruri z. Acest fapt este interpretat uneori in sensul ca transformarea in scoruri z a unei oricarei distributii o transforma intr-o distributie normala. Este o concluzie gresita. Convertirea valorilor unei distributii in scoruri z nu modifica forma distributiei. Distributia normala z este o distributie teoretica in timp ce o distributie z oarecare are forma distributiei valorilor originale.