ESANTIONAREA SI DISTRIBUTII DE ESANTIONARE

Dupa cum am aratat in capitolul 1, cercetatorii folosesc statistici inferentiale pentru a trage concluzii despre caracteristicile unei populatii pe baza caracteristicilor corespunzatoare ale unui esantion din acea populatie. Folosirea adecvata a acestor tehnici statistice cere ca esantioanele sa fie selectate aleatoriu[1] din populatiile de referinta. In cazul cel mai general, un esantion este aleatoriu daca fiecare caz din populatia de referinta are aceeasi probabilitate de a fi selectat in esantion cu a oricarui alt caz si selectarea fiecarui caz este independenta de selectarea tuturor celorlalte cazuri. Daca populatia are, sa zicem, 1000 de membri, atunci fiecare membru trebuie sa aiba o probabilitate de 1/1000 de a fi selectat. Supozitia fundamentala a statisticilor inferentiale este aceea ca investigarea unui esantion aleatoriu dintr-o populatie conduce la rezultate apropiate de cele care ar fi obtinute daca ar fi investigata intreaga populatie si, dupa cum vom vedea, notiunea de distributie de esantionare furnizeaza o masura a acestei apropieri. Esantioanele nealeatorii pot fi foarte usor alcatuite, dar nu permit formularea unor concluzii despre populatiile respective, ci doar despre esantioane.

De notat ca in acest context, "aleatoriu" este un termen tehnic, care nu are acelasi inteles cu termenul "intamplator", asa cum este utilizat acesta in limbajul obisnuit. Un esantion aleatoriu nu este alcatuit la intamplare, ci printr-un proces bine determinat si precis de selectie. De pilda, intervievarea unor persoane pe care se intampla sa le intalnim intr-un supermagazin nu constituie o esantionare aleatorie.

Selectia aleatorie este o conditie necesara pentru obtinerea unor esantioane care sa ofere imagini cat mai precise ale populatiilor de referinta sau, altfel spus, a unor esantioane reprezentative pentru populatiile de referinta, dar nici macar cele mai sofisticate proceduri de selectie aleatorie nu garanteaza 100% ca esantionul respectiv este o reprezentare exacta a populatiei din care a fost alcatuit. Totusi, probabilitatea ca esantioanele aleatorii sa fie reprezentative pentru populatiile de referinta este foarte mare, iar tehnicile statistice permit determinarea precisa a probabilitatilor erorilor de reprezentativitate.

Inainte de a prezenta rolul esantionarii in statisticile inferentiale, vom prezenta pe scurt cateva dintre cele mai utilizate procedee de esantionare aleatorie.

1 PROCEDEE DE ESANTIONARE ALEATORIE

Procedeul fundamental de esantionare aleatorie se numeste esantionare aleatorie simpla. In procesul de selectie a unui esantion aleatoriu simplu, fiecare caz din populatia de referinta are o probabilitate egala de a fi inclus in esantion, iar selectarea fiecarui caz este independenta de selectarea tuturor celorlalte cazuri. Procesul de selectie aleatorie simpla se poate baza pe diferite tipuri de operatii. In mod tipic, se folosesc tabele cu numere selectate aleatoriu de un computer. Un exemplu de astfel de tabel este dat in Anexa B. Aceste tabele contin numere alcatuite din cinci cifre, de la 0 la 9. Pentru a folosi un astfel de tabel, se atribuie fiecarui caz din populatia de referinta un numar unic de identificare, dupa care se alege la intamplare un rand si o coloana din tabel si, pornind de la acel punct la dreapta sau la stanga, in sus sau in jos, se citesc numerele, selectand in esantion cazurile ale caror numere de identificare corespund cu numerele citite in tabel. Selectia se opreste atunci cand s-a ajuns la dimensiunea dorita a esantionului. Pentru ilustrare, sa presupunem ca dorim sa alcatuim un esantion de dimensiune n = 20 dintr-o populatie de dimensiune N = 600. Mai intai, numerotam membrii populatiei intr-o ordine oarecare 001, 002, ., 600. Pentru a forma esantionul, consideram doar ultimele trei cifre ale numerelor din tabel si, evident, ignoram numerele mai mari de 600. Alegem la intamplare un rand si o coloana si incepem selectia pornind de la numarul respectiv si mergand, de pilda, in jos pe coloana aleasa, pana cand obtinem 20 de numere. Daca un numar de identificare este selectat mai mult decat o singura data, se ignora repetarea si se trece la urmatorul numar din secventa[2]. Esantionul va fi alcatuit din acei membri ai populatiei ale caror numere de identificare au fost astfel selectate.

Statisticienii atrag atentia asupra necesitatii de a schimba des tabelul cu numere aleatorii, daca cercetatorul foloseste des procedeul mentionat: "Natura umana este in asa fel, incat fiecare dintre noi are tendinta de a porni aproximativ din acelasi loc si de a parcurge repetat aproximativ aceeasi cale. De aceea, folosirea repetata a aceluiasi tabel poate sa conduca la selectarea aceluiasi sir de numere"[3].

Sa vedem acum cum poate fi folosit tabelul cu numere aleatorii pentru a repartiza aleatoriu un numar de subiecti in grupuri. Sa presupunem ca avem 15 subiecti si, in vederea unui experiment, dorim sa alcatuim trei grupuri cu cate cinci subiecti in fiecare grup. Pentru aceasta, alegem la intamplare un rand si o coloana si, urmand o anumita directie, atribuim un numar fiecarui subiect, considerand doar ultimele doua cifre ale numerelor din tabel. Apoi, consideram subiectii in ordinea crescatoare a numerelor atribuite si repartizam primii cinci subiecti in grupul 1, urmatorii cinci subiecti in grupul 2 si ultimii cinci subiecti in grupul 3. Tabelul urmator prezinta o posibila repartizare de felul mentionat:

Evident, procedeul poate fi folosit pentru orice numar de grupuri intr-un experiment.

Procedura de esantionare aleatorie simpla devine incomoda, atunci cand dimensiunea populatiei de referinta este foarte mare (10000, de pilda). Intr-un astfel de caz se poate folosi esantionarea sistematica, numita si selectie mecanica. Mai intai, se stabileste o fractie de selectie (fractie de esantionare, pas de numarare): K = N/n, in care N este numarul total de cazuri din populatia de referinta, iar n este dimensiunea dorita a esantionului. De pilda, daca N = 10000 si n = 300, K = 34 (K se rotunjeste intotdeauna pana la un numar intreg). Dupa ce s-a stabilit pasul de numarare, se listeaza la intamplare membrii populatiei de referinta si se alege la intamplare, eventual prin tragere la sorti, un caz din primele K cazuri care se include in esantion si apoi se alege fiecare al K lea caz pentru a fi inclus in esantion pana se ajunge la dimensiunea dorita a esantionului. In exemplul nostru, daca din primele 34 de cazuri a fost ales la intamplare cazul cu numarul 5, atunci se vor include in esantion urmatoarele cazuri: 5, 39, 73, 107, s.a.m.d. pana la n = 300.

De notat ca in cazul esantionarii sistematice, selectia nu mai este independenta, deoarece, cu exceptia primului caz, fiecare caz selectat depinde de numarul de ordine al cazului precedent. De aceea, acest procedeu este considerat ca fiind cvasialeatoriu. Caracterul aleatoriu este asigurat prin alcatuirea intamplatoare a listelor din care sunt selectate cazurile.

Un al treilea procedeu de esantionare, esantionarea stratificata, conduce la cresterea cantitatii de informatie despre populatie. Pentru a alcatui un esantion aleatoriu stratificat, se clasifica populatia de referinta dupa criterii relevante si se alcatuiesc esantioane aleatorii simple din fiecare clasa (strat). De pilda, pot fi folosite criterii precum sexul, varsta sau ocupatia.

Cititorul interesat de detalii privitoare la procedurile de esantionare descrise sumar mai sus sau/si de alte procedee de esantionare poate consulta carti despre esantionare sau manuale de metodologie a cercetarii psihologice.

2 DISTRIBUTIA DE ESANTIONARE

Scopul principal al statisticilor inferentiale este generalizarea unor caracteristici ale esantionului la populatia din care a fost alcatuit. Strategia generala a acestor tehnici statistice consta din trecerea de la distributia unui esantion la distributia unei populatii prin intermediul notiunii de distributie de esantionare. Stim ca informatia necesara pentru caracterizarea adecvata a unei distributii include forma distributiei, unele marimi ale tendintei centrale si unele marimi ale dispersiei Distributia unui esantion este empirica (exista in realitate) si cunoscuta, esantionul fiind alcatuit de cercetator, in timp ce distributia populatiei este empirica, dar este necunoscuta. Dupa cum vom vedea, distributia de esantionare este non-empirica (teoretica - nu poate fi obtinuta niciodata in realitate de catre cercetator), iar pe baza legilor de probabilitate pot fi deduse forma, tendinta centrala si dispersia acestei distributii, astfel ca proprietatile sale pot fi exact cunoscute. Sa explicam.

In capitolul anterior am folosit distributia normala standard pentru a descrie distributii de scoruri ale unor variabile aproximativ normale. In cele ce urmeaza vom considera mediile aritmetice, nu scorurile individuale, si vom folosi distributia normala standard (distributia Z) pentru a descrie distributia mediilor aritmetice () pentru toate esantioanele posibile de dimensiune data (n), care pot fi obtinute aleatoriu dintr-o populatie. Cu alte cuvinte, vom considera ca media aritmetica este ea insasi o variabila, ale carei scoruri sunt mediile aritmetice ale tuturor esantioanelor aleatorii posibile de dimensiune constanta n dintr-o populatie.

Sa presupunem ca ne intereseaza media aritmetica a varstelor dintr-o populatie de dimensiune comparabila cu populatia Romaniei. Selectam un esantion aleatoriu de 100 de persoane din aceasta populatie si inregistram varstele pentru acest esantion. Evident, ceea ce am obtinut este distributia varstelor pentru esantionul considerat, pentru care putem calcula media aritmetica. Acum, sa presupunem ca am selectat (cu inlocuire) toate esantioanele posibile de dimensiune 100 din populatia respectiva si ca am calculat media aritmetica pentru fiecare esantion. Rezultatele pe care, in principiu, le-am obtine in acest fel constituie distributia mediilor aritmetice pentru toate esantioanele posibile de dimensiune 100 din populatia de referinta. Aceasta distributie este numita distributia de esantionare a mediilor aritmetice ale tuturor esantioanelor aleatorii de dimensiune 100 din populatia de referinta. In general, distributia de esantionare a mediilor aritmetice se defineste ca distributia mediilor aritmetice ale tuturor esantioanelor aleatorii de dimensiune constanta n din populatia de referinta. In mod similar, se definesc distributiile de esantionare pentru alte marimi statistice (proportii, coeficienti de corelatie etc.), pe care le vom considera in unele dintre capitolele care urmeaza. In continuare, ne vom concentra atentia asupra distributiei de esantionare a mediilor aritmetice.

Ca si distributiile de frecvente considerate pana acum, distributia de esantionare a mediilor aritmetice (si cele ale celorlalte marimi statistice) are (1) o forma, (2) o medie aritmetica si (3) o abatere standard. Pentru media aritmetica si abaterea standard a distributiei de esantionare a mediilor aritmetice vom folosi, respectiv, simbolurile si .

Cei trei parametri mentionati ai distributiei de esantionare a mediilor aritmetice sunt dati de urmatoarea teorema, numita teorema limitei centrale:

Daca se alcatuiesc toate esantioanele posibile de dimensiune n dintr-o populatie cu media aritmetica μ si abaterea standard σ, atunci distributia de esantionare a mediilor aritmetice ale acestor esantioane are urmatoarele trei proprietati:

1.     Media sa aritmetica,, este egala cu media aritmetica a populatiei, μ..

2.     Abaterea sa standard,, este egala cu .

3.     Cu cat n este mai mare, cu atat forma sa aproximeaza mai bine normalitatea, indiferent de forma distributiei populatiei.

Demonstrarea acestei teoreme depaseste cadrul propus pentru lucrarea de fata. Pentru concizia exprimarii, in loc de "distributia de esantionare a mediilor aritmetice" vom scrie in continuare "distributia de esantionare a ".

Teorema limitei centrale arata ca, indiferent de forma distributiei unei variabile intr-o populatie, distributia de esantionare a va fi aproximativ normala pentru esantioane suficient de mari. De pilda, daca lucram cu o variabila care prezinta o distributie asimetrica, precum venitul, putem sa presupunem ca distributia de esantionare a este aproximativ normala pentru esantioane cu n 100, avand media aritmetica egala cu cea a populatiei si abaterea standard egala cu . Astfel, teorema limitei centrale elimina constrangerea normalitatii pentru populatii. Daca distributia unei variabile este aproximativ normala, atunci distributia de esantionare a va fi aproximativ normala chiar si pentru valori mai mici ale lui n. In fine, teoretic vorbind, daca distributia unei variabile este riguros normala, atunci distributia de esantionare a va fi normala indiferent de dimensiunea esantionului.

3 DETERMINAREA PROBABILITATILOR PENTRU

MEDII ARITMETICE

Teorema limitei centrale poate fi utilizata pentru a determina probabilitatea de a selecta la intamplare o medie aritmetica a unui esantion de dimensiune data, cuprinsa intr-o anumita plaja de medii aritmetice. Pentru ilustrare, sa consideram o populatie cu media aritmetica a unei caracteristici aproximativ normale μ = 117 si σ = 14. Sa presupunem ca ne intereseaza probabilitatea ca un esantion aleatoriu cu n = 36 selectat din aceasta populatie sa aiba media aritmetica a caracteristicii respective cuprinsa intre 115 si 120. Intrucat variabila considerata este aproximativ normala, conform punctului 3 al teoremei limitei centrale distributia de esantionare a aproximeaza normalitatea pentru n = 36. Conform punctelor 1 si 2 ale acestei teoreme, avem:

= 117

In paragraful 4.4.2 am lucrat cu formula

pentru a determina probabilitatea de selectie a unui scor cuprins intr-o plaja data de scoruri ale unei distributii aproximativ normale. Aici, valorile 115 si 120 sunt medii aritmetice. Scorurile Z corespunzatoare acestor valori se calculeaza cu ajutorul urmatoarei formule:

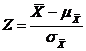
In exemplul nostru, avem:

Din tabelul curbei normale aflam ca probabilitatea corespunzatoare scorului Z = 0,85 este 0,3023 si ca probabilitatea corespunzatoare scorului Z = +1,28 este 0,3997. Ca atare, probabilitatea ca un esantion cu n = 36 sa aiba media aritmetica intre 115 si 120 este de 0,7020 (0,3023 + 0,3997).

Sa notam si aici ca pentru determinarea probabilitatilor de selectare a mediilor aritmetice se utilizeaza aceleasi proceduri ilustrate pentru determinarea procentelor de cazuri. De pilda, probabilitatea ca un esantion aleatoriu cu n = 36 selectat din populatia considerata mai sus sa aiba media aritmetica peste 120 este de 0,1003 (0,5000 0,3997).

4 STRATEGIA INFERENTIALA

In statisticile inferentiale, marimile statistice pentru populatii sunt numite parametri si, prin contrast, marimile statistice pentru esantioane sunt numite pur si simplu statistici. Figura 1 ilustreaza strategia generala a statisticilor inferentiale[4], pe care o vom folosi in capitolele care urmeaza.

Figura 1 Strategia inferentiala

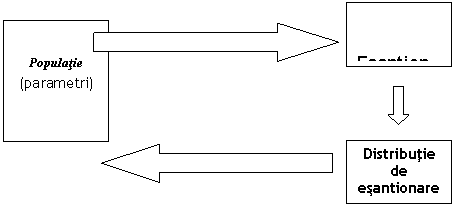
Astfel, in general, in statisticile inferentiale avem o populatie ai carei parametri se doresc a fi determinati. Pentru aceasta, selectam un esantion aleatoriu din acea populatie si calculam statisticile care reflecta parametrii corespunzatori, dupa care, pe baza distributiilor de esantionare ale acelor statistici si a legilor de probabilitate inferam asupra parametrilor populatiei.

GLOSAR

Distributia de esantionare a mediilor aritmetice: distributia mediilor aritmetice ale tuturor esantioanelor aleatorii de dimensiune constanta n din populatia de referinta. In mod similar, se definesc distributiile de esantionare pentru alte marimi statistice (proportii, coeficienti de corelatie etc.).

Esantionare aleatorie simpla: metoda de selectie a unui esantion in care fiecare caz din populatia de referinta are o probabilitate egala de a fi inclus in esantion, iar selectarea fiecarui caz este independenta de selectarea tuturor celorlalte cazuri.

Esantionare sistematica: metoda de selectie a unui esantion in care primul caz dintr-o lista a populatiei de referinta este selectat aleatoriu, dupa care este selectat fiecare al k-lea caz.

Esantionare stratificata: metoda de selectie a unui esantion in care populatia de referinta este clasificata dupa criterii relevante si se alcatuiesc esantioane aleatorii simple din fiecare clasa (strat).

Parametri: marimi statistice pentru populatii; prin contrast, marimile statistice pentru esantioane sunt numite statistici.

Teorema limitei centrale: teorema care specifica media aritmetica, abaterea standard si forma distributiei de esantionare a mediilor aritmetice.