Solicitari axiale - piese

Solicitari axiale - piese

In cazul solicitarilor axiale, piesele, respectiv elementele de constructii, sunt solicitate de forte care lucreaza dupa axa acestora. Solicitarea poate fi de intindere sau compresiune (fig. 55).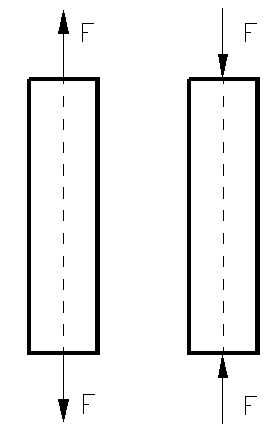

Figura 55

Fortele axiale sunt considerate pozitive pentru solicitarea de intindere si negative pentru solicitarea de compresiune. Forta axiala poate fi constanta sau variabila in lungul barei, depinde de incarcatura exterioara a barei. Valoarea fortei axiale , in dreptul unei sectiuni a barei este data de suma proiectiilor pe axa barelor a tuturor fortelor situate la dreapta sau la stanga sectiunii considerate. Pentru ca solicitarea de compresiune sa nu fie denaturata, prin aparitia altor fenomene , lungimea barelor trebuie sa indeplineasca conditia

l 5.b_min , unde ( l ) fiind lungimea barei, iar ( b_min ) este dimensiunea cea mai mica a sectiunii transversale.

Variatia fortei axiale de-a lungul barei de regula, se reprezinta

printr-o diagrama dupa cum se va arata in exemplele urmatoare.

Sectiunile transversale ale barelor pot fi constante sau variabile, cand sectiunile au o forma complicata este mai greu de prelucrat , deci si in mod implicit mai greu de executat .

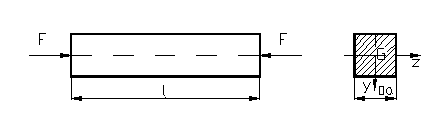
Figura 56

Problema nr.1

Sa se traseze diagrama de forte axiale pentru bara incarcata ca in figura 57 , bara este incastrata la un capat si asupra ei actioneaza fortele dirijate dupa axa barei ca in figura.

Figura 57

S-au notat cu literele A, B, C, D, E, G sectiunile in care se aplica anumite forte, se calculeaza valoarea fortei axiale pe fiecare portiune de bara:

Regiunea intai ; x₁ ; N(x₁) = F _.

Regiunea a II-a ; x₂ ; N(x₂) = F -2F=-F .

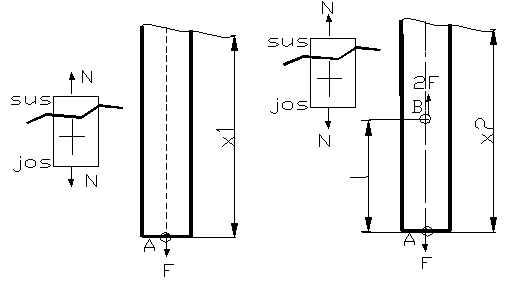
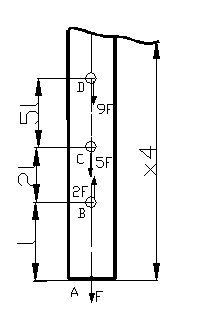
Figura 58

Figura 59

Regiunea a III-a ; x₃ ; N(x₃) = F-2F+5F = 4F ;

Regiunea a IV-a ; x₄ ; N(x₄) = F-2F+5F +9F= 13F ;

Regiunea a V-a ; x₅ ; N(x₄) = F-2F+5F +9F-3F= 10F .

Diagrama arata ca forta axiala este maxima pe portiunea D-E , in sectiunea in care avem forta exterioara axiala concentrata trebuie ca in diagrama de forte interioare axiale sa existe salt . Valoarea absoluta a saltului trebuie sa fie egala cu valoarea absoluta a fortei exterioare concentrata din acea sectiune . Deci saltul S= , in sectiunea din punctul A avem salt S^A = F, in sectiunea din punctul B avem saltul S^B = = 2F , la fel se procedeaza si in celelalte sectiuni.

Problema nr.2

Se considera cazul unei bare verticale de forma conica , solicitata numai de greutatea proprie si rezemata ca in figura 60.

Din figura (61) diametrul d(x) = D. ,γ este greutatea specifica a barei ( exprimata in ). Forta axiala in sectiunea curenta ( x) este: N(x) = x³, unde x(0, l), aceasta expresie se obtine prin metoda integrarii . N(x) = = = N_{max ;}

N(x) = 0; dG(x) = γ . A(x) . dx ;   

A(x) = ;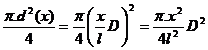

dG(x) = γ . .dx . Din figura 62 se face proiectia pe axa OY :

N(x) + dG(x)-[N(x)+dN(x)] =0 ;de unde rezulta:

dN(x)= dG(x), se integreaza ;

Figura 60

=x³ + C = N(x);

; C = 0 , deci N(x) = x³ ; Se traseaza graficul functiei N(x) in mod normal , tinand cont ca avem planul [xON(x)]. N^’(x)=(x²) ; iar derivata a II-a

Figura 61

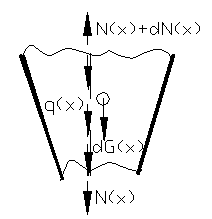
Figura 62

N’’(x)=.x > 0 ; fiind convexa pe domeniul maxim de definitie. Forta de reactiune din incastrarea din punctul (A) reiese direct din diagrama de forte axiale , anume .

Problema nr.3

Se considera cazul unei bare incastrata la un capat si libera la celalalt capat, asupra careia actioneaza forte distribuite axial dupa functia : x(y) = q₀ . y³ , forte axiale concentrate ca in figura 63. Se dau : q₀= 0,2 kN/m; F = 1 kN.

Sa se traseze diagramele de eforturi pentru aceasta bara din figura 63.

Rezolvare:                    

Aflam forta de reactiune din incastrare , notata cu H_A din conditia de echilibru: = 0 H_A –R_V –5F +F = 0unde R_V=;

R_V = 0,15 kN;H_A – 0,15 kN –5F +F = 0 H_A= 4,15 kN . Fortele concentrate , fortele ditribuite , impart bara in regiuni , in cazul acesta exista 3 regiuni : intaii , a II-a , a III-a.

Regiunea sau zona intai unde variabila x₁( 0; 0,2m ) din figura 64

A₁ + A₂ = x.y; x(y) = q₀ y³; A₁ = ; A₁ = 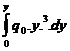= q₀.y⁴/4=q₀ = ; iar y(x) = ; q₀ = 0,2 ; ; A₂ =

x.y – A₁ ; A₂ = x. - = 3; R_V (x) = 3= A₂ .

Se mai poate calcula si cu metoda sectiunilor plane , aceasta metoda fiind cel mai des folosita pentru calculul eforturilor . Se ia numai portiunea de bara incarcata pe lungimea infinitezimala d(x) din figura 65. In sectiunile interioare de la capatul de lungime (x) , respectiv [x+d(x)], apar eforturile N(x), repectiv N(x)+dN(x).

Din conditia de echilibru a barei = 0 se obtin relatiile diferentiale intre sarcini si eforturi pentru solicitarea axiala.

Figura 64

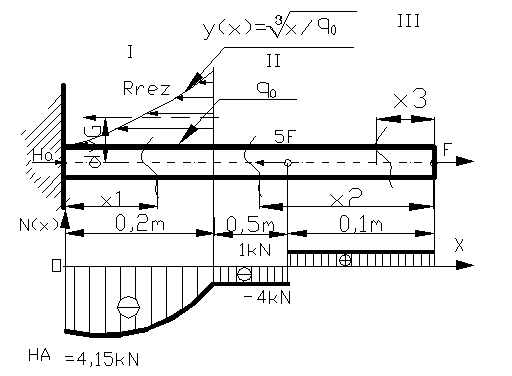
Figura 63

Figura 65

3.1.1. Relatiile diferentiale intre sarcini si eforturi pentru solicitarea axiala

Din figura 65 rezulta :

N(x) + dR_V –( N(x) + dN(x) ) = 0 ; N(x) + dR_V – N(x) – dN(x) = 0 ; dR_V = dN(x); ; N(x) = R_V(x) +C₁ , dR_V(x) = y.d(x)= d(x) ; N(x)=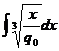 ; N(x) = 3 + C₁ , constanta C₁ , o determinam din conditiile initiale ale lui Cauchy C₁= N(x) = - H_A ,C₁= -4,15kN , N(x) = 3-4,15 kN, trasam graficul fuctiei N(x) in planul [XON(x)]; N(x) = -4,15 kN N(x) = -4kN ;

N^’(x) = ;N^’’(x) = 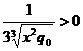, convexa.

Regiunea a II –a

N(x₂) = F – 5F = - 4 F = - 4 kN.

Regiunea a III –a

N(x₃) = F = 1 kN.

In aceste probleme trebuie ca dy_G sa fie foarte mic pentru ca sa nu avem solicitari compuse si q₀ trebuie sa fie foarte mic , anume de

2.10^-3 N/m; sau 2 .10^-4 N/m . Pentru stabilirea relatiilor de calcul ale rezistentei materialelor, la oricare dintre solicitari, se parcurg urmatoarele etape:

in prima etapa, se stabileste legea de distributie a eforturilor unitare pornind de la anumite ipoteze de deformatie, verificate experimental.

dupa stabilirea legii de distributie, se scriu ecuatiile de echivalenta , in sectiune , intre eforturile concentrate

( N; T; M_i; M_t ) si cele rezultand din insumarea infinitatii de forte elementare , produse de eforturile unitare si aplicate pe suprafetele elementare dA.