
|
|
|
INTERSECTIA SUPRAFETELOR POLIEDRALE SI CILINDRO-CONICE
1. Generalitati
Formele obiectelor rezulta prin combinarea diferitelor suprafete (corpuri geometrice) in functie de cerintele functionale, posibilitatile de prelucrare si cerintele ergonomice si estetice. Din punctul de vedere al proiectarii si reprezentarii pieselor unui ansamblu mecanic insusirea modului de rezolvare a problemelor de intersectie a suprafetelor este importanta deoarece:
- analizand o piesa mecanica se pot identifica suprafetele / corpurile geometrice care o compun, dimensiunile acestora si se pot preciza pozitiile lor reciproce, reprezentarea si cotarea piesei devenind un proces rational si nu bazat pe intuitie;
- se pot reprezenta corect diferitele muchii (drepte sau curbe) rezultate prin intersectia suprafetelor anterior identificate.
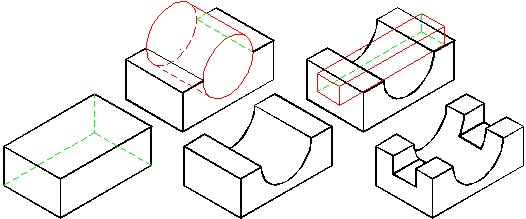
Fig. 1
In fig. 1 este prezen-tata generarea for-mei geometrice a unui corp de lagar. Din corpul geometric de baza (o prisma dreapta dreptunghiu-lara) se extrage un cilindru circular drept iar din corpul rest se extrage in continua-re o alta prisma.
Plecand de la notiunile bine cunoscute:
Definitii
Reuniunea A U B este multimea obiectelor care sunt elemente a cel putin uneia din multimile A , B
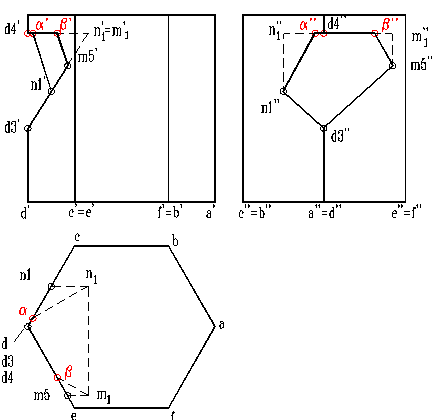
Intersectia A ∩ B este multimea obiectelor care sunt totodata elemente ale lui A si ale lui B
Diferenta A B este multimea obiectelor care sunt elemente ale lui A si nu ale lui B
este evident ca si in grafica asistata operatiile cu suprafete sau solide sunt operatii asupra multimilor de puncte ale acestora, adica: reuniunea, intersectia si diferenta.
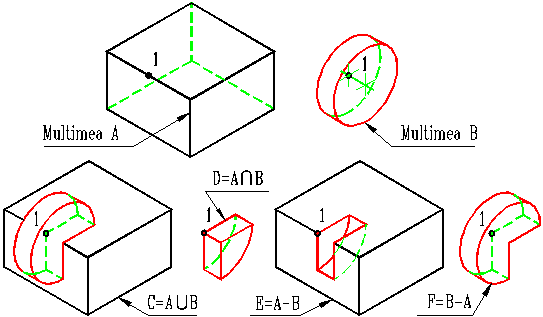
Fig. 2
Reuniunea a doua corpuri este operatia de generare a unui nou obiect care se caracterizeaza printr-un volum egal cu suma volumelor necomune a celor doua.
In fig. 2 corpul rezultat prin reuniunea prismei si cilindrului are volumul egal cu volumul prismei si trei patrimi din volumul cilindrului.
Intersectia a doua corpuri este operatia de generare a unui nou corp ce reprezinta partea comuna a celor doua corpuri initiale.
In fig. 2 rezultatul intersectiei dintre prisma si cilindru reprezinta un sfert din cel din urma.
Diferenta a doua corpuri este operatia de generare a unui nou corp care reprezinta restul ramas dupa eliminarea din unul din corpuri a portiunii comune dintre cele doua corpuri.
In fig. 2 diferenta prisma - cilindru este un corp avand volumul egal cu volumul prismei mai putin o patrime din volumul cilindrului.
In geometria descriptiva toate trei operatiile se regasesc sub aceeasi denumire generica de "intersectia suprafetelor" si au drept scop construirea curbelor de intersectie dintre suprafetele care marginesc piesele. Deoarece in constructia de masini sunt utilizate preponderent suprafete cilindro-conice, de rotatie si poliedrale dintre cele mai simple iar dispunerea lor este de cele mai multe ori particulara, in continuare se va prezenta o singura metoda de rezolvare grafica a problemelor de intersectie a suprafetelor, care poate fi utilizata in majoritatea situatiilor intalnite in practica: metoda planelor auxiliare de sectiune, al carui principiu a fost deja prezentat.
2 Metoda generala de rezolvare a problemelor de intersectie
Fiind date doua suprafete (poliedrale sau cilindro-conice) se cere sa se determine multimea punctelor curbei (sau curbelor) lor de intersectie. Fiecare dintre aceste puncte rezulta ca intersectie a doua drepte, fiecare apartinand uneia dintre suprafete. Pentru ca sunt drepte concurente, ele determina un plan. Metoda planelor auxiliare de sectiune consta intr-un algoritm de construire si folosire a acestor plane auxiliare. Se cauta sa se construiasca acele plane care sectioneaza ambele suprafete dupa drepte, muchii sau generatoare ale lor.
Daca ambele suprafete care se intersecteaza sunt prismatice sau cilindrice, planele auxiliare de sec-tiune sunt plane paralele cu un plan imaginar, determinat de doua drepte, fiecare paralela cu muchia sau respectiv axa uneia dintre suprafetele. Astfel, fiecare plan auxiliar va sectiona longitudinal ambele suprafete dupa muchii (sau drepte) si respectiv generatoare ale lor.
Daca o suprafata este prismatica (sau cilindrica) si cealalta este piramidala (sau conica) planele auxiliare de sectiune sunt plane concurente intre ele, fiecare continand varful piramidei (sau conului) si o dreapta paralela cu muchia prismei (sau axa suprafetei cilindrice). Astfel, fiecare plan auxiliar va sectiona suprafetele dupa muchii, drepte sau generatoare ale lor.
Daca ambele suprafete sunt piramidale sau conice, planele auxiliare sunt cele care contin dreapta determinata de varfurile suprafetelor, astfel incat fiecare plan auxiliar sectioneaza suprafetele dupamuchii, drepte sau generatoare ale lor.
In continuare se va exeplifica folosirea metodei planelor auxiliare de sectiune.
3. Intersectia suprafetelor poliedrale
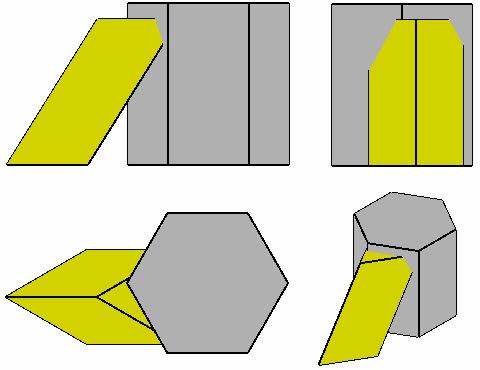 EXEMPLUL NR. 1
EXEMPLUL NR. 1
Sa se reprezinte corpul rest obtinut prin diferenta dintre doua prisme cu bazele cu-prinse in [H]:
i) o prisma dreapta verticala cu baza ABCDEF hexagon regulat si inaltimea de 60 mm;
ii) o prisma MNPM1N1P1 frontala cu baza triunghi echilateral. Se cunosc coor-donatele: A(10, 40, 0), D(70, 40, 0), M(85, 27, 0), N(85, 62, 0), P1 (81, 45, 54).
Rezolvare
In figura 3 este prezentat modelul celor doua pris-me. Folosind metoda planelor auxiliare de sectiune, se cauta sa se intersecteze prismele cu plane care le parcurg longitudinal. Fig. 3
Etapele de rezolvare sunt:
a) reprezentarea celor doua prisme si determinarea tipului si numarului planelor auxiliare de sectiune,
b) determinarea varfurilor poligonului spatial de intersectie,
c) rezolvarea vizibilitatii epurei si reprezentarea corpului rest.
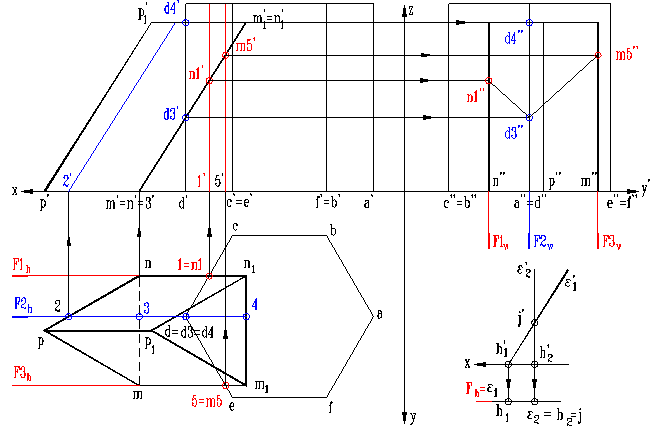
a) Reprezentarea
celor doua prisme, determinarea tipului si numarului planelor
auxiliare de sectiune
Fig. 4 Fig. 5
In epura din figura 4 sunt reprezentate cele doua prisme. Prisma verticala hexagonala are, in proiectia verticala, muchiile B si F, C si E confundate, vizibile fiind E si F, iar in proiectia laterala sunt confundate muchiile C si B, D si A, E si F, vizibile fiind C, D, E. Prisma triunghiulara oblica are fata MNN1M1 plan de capat si deci proiectiile verticale ale muchiilor M si N sunt confundate, vizibila fiind muchia M. In proiectia orizontala este invi-zibila doar muchia MN.
Planele auxiliiare de sectiune sunt plane definite de doua drepte concurente construite fiecare paralela cu muchiile uneia dintre prisme. In figura 5 este prezentata determinarea tipului de plan auxiliar astfel:
- dreapta E1 (ε1 , ε'1) PP1 intersecteaza in J dreapta E2 (ε2 , ε'2) AA1, determinand astfel un plan;
- se construiesc si se noteaza cu H1 si H2 urmele orizontale ale dreptelor E1 si E2;
- urmele H1 si H2 determina urma orizontala a planului cautat. Se constata ca planul este un plan de front.
La aceasta concluzie se putea ajunge si direct pentru ca sectionarea longitudinala a prismei oblice se poate face doar cu plane de front sau de capat, in timp de prisma verticala poate fi sectionata longitudinal doar cu plane de front sau de profil, rezultand ca numai un plan de front poate sectiona longitudinal ambele prisme.
Se construiesc plane de front prin fiecare dintre muchiile care participa la intersectie, adica:
- prin muchiile NN1 si MM1 ale prismei oblice (segmentul PP1 nu intersecteaza prisma verticala); planele [F1] si [F3];
- prin muchia DD1 planul [F2].
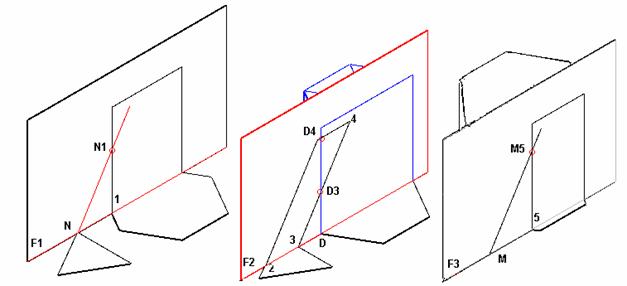
b) Determinarea varfurilor poligonului spatial de intersectie (figurile 4, 6, 7)
Modul in care rezulta varfurile poligonului de intersectie este prezentat intuitiv cu ajutorul aceluiasi model 3D in figura 6.
i)
Planul [F1] contine muchia NN1 si sectioneaza
prisma hexagonala dupa segmentul vertical notat 1. Varful N1 al
poligonului de interesctie rezulta la intersectia muchiei NN1
cu segmentul 1, ![]() (figura 6a).
(figura 6a).
ii)
i) Planul [F3] contine muchia MM1 si sectioneaza
prisma hexagonala dupa segmentul vertical notat 5. Varful M5 al
poligonului de interesctie rezulta la intersectia muchiei MM1
cu segmentul 5, ![]() (figura 6c).
(figura 6c).
iii)
) Planul [F2] contine muchia DD1 si sectioneaza
prisma oblica dupa segmentele de front notate 2 si 3 iar ba-za
superioara M1N1P1 dupa segmentul
notat 4. Muchia DD1 nu intersecteaza segmentul 2 ci doar
segmentul 3, rezultand punctul D3, ![]() . Muchia DD1 taie segmentul 4 rezultand varful D4,
. Muchia DD1 taie segmentul 4 rezultand varful D4,
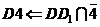 ,
,  (vezi figura 6b).
(vezi figura 6b).
Fig. 6a Fig. 6b Fig. 6c
Pentru
a determina si celelalte varfuri ale poligonului spatial se
observa (figura 7)
ca muchia M1N1 a bazei superioare
intersecteaza
planul vertical al fetei CDD1C1 in punctul notat a
si planul vertical al fetei DEE1D1 in punctul
notat b, adica:![]() si
si ![]() .
.
Fig. 7
Se construiesc toate proiectiile varfurilor poligonului de intersectie si se unesc in ordinea planelor de sctiunea care le contin si a fetelor unuia dintre poliedre, adica: N1, D3, M5, b, D4, a, N1.
Se analizeaza vizibilitatea fiecarei laturi a poligonului spatial, pe fiecare dintre planele de proiectie.
i) In proiectia orizontala sunt vizibile laturile b - D4 si D4 - a, pentru ca sunt segmente care apartin unei fete vizibile (baza superioara a prismei oblice) si nu sunt acoperite de hexagonul bazei superioare.
ii) In proiectia verticala sunt vizibile laturile D3 - M5 si M5-b pentru ca sunt segmente care apartin unei fete vizibile - PMM1P1. Latura b-D4 este deasemenea vizibila.
 iii) In proiectia
laterala sunt vizibile segmentele N1-a
- D4 - b - M5, pentru ca
apartin fetelor vizibile.
iii) In proiectia
laterala sunt vizibile segmentele N1-a
- D4 - b - M5, pentru ca
apartin fetelor vizibile.
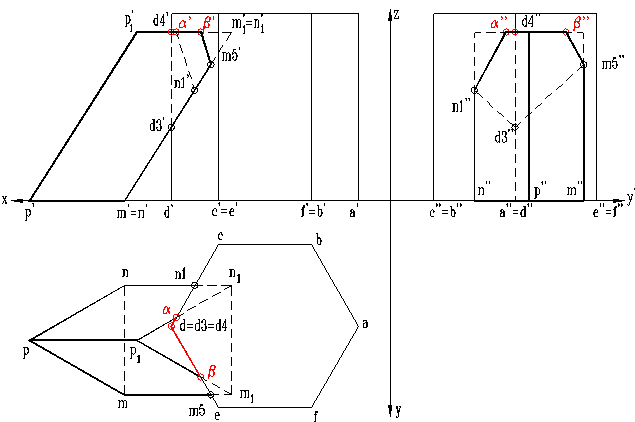
c) Rezolvarea vizibilitatii epurei si reprezentarea corpului rest (figurile 7 si 8)
Se completeaza vizibilitatea laturi-lor poligonului de intersectie cu cea a muchiilor care participa la intersectie, tinand cont si de pozi-tia relativa a corpurilor.
i) In proiectia orizontala este invi-zibila portiunea prismei oblice din interiorul prismei hexagonale.
ii) In proiectia verticala este invizi-bila portiunea D3-D4 pentru ca se gaseste in interiorul prismei oblice.
iii) In proiectia laterala este invi-zibila muchia DD1 pentru ca este acoperita de prisma oblica.
Fig. 8
4. Intersectia suprafetelor cilindro-conice
 EXEMPLUL NR. 1
EXEMPLUL NR. 1
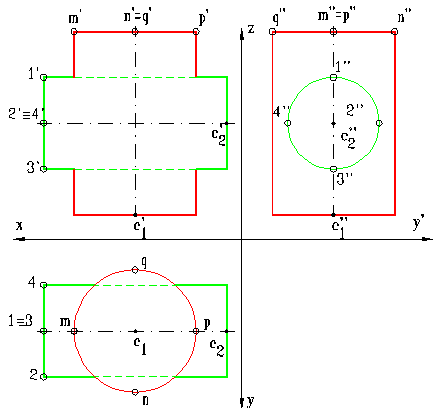
Sa se intersecteze doi cilindri cir-culari drepti definiti astfel:
-cilindrul C1 are axa dreapta ver-ticala, centrul bazei in C1(35, 30, 8), r = 20 mm si inaltimea 60 mm;
-cilindrul C2 are axa dreapta fron-to-orizontala,centrul bazei in C2(5, 30, 38), r = 15 mm si inaltimea 60 mm.
Datele initiale sunt transpu-se in epura din figura 9, in figura 10 este prezentata rezolvarea grafica in epura iar in figura 11 este mode-lat principiul metodei planelor auxi-liare de sectiune.
Planele auxiliare de sectiune sunt, in acest caz plane de front deoa-rece planul determinat de o dreapta verticala (paralela la axa cilindru-luiC1 ) concurenta cu o dreapta fronto-orizontala (paralela la axa ci-lindrului C2 ) este un plan de front.
Fig. 9
In figura 10 se prezinta constructia planului [A] D1 U D2, unde D1 si D2 sunt fiecare paralela cu axa unui cilindru.
Planele auxiliare [Q1], [Q2], [Q3] folosite pentru rezolvare sunt construite prin generatoarele de contur aparent ale cilindrului C2 deoarece acesta strapunge cilindrul C1. In continuare este explicata constructia uneia dintre curbele de intersectie α - β - γ - δ, cealalta curba fiind identica. Curba de intersectie nu este o curba plana (si mai ales nu este un cerc) ci este o curba spatiala.
a) Din intersectia planului [Q1] cu C1 rezulta generatoarea R iar din intersectia planului [Q1] cu C2 rezulta generatoarea 2, din intersectia lor rezultand punctul β (β, β', β'').
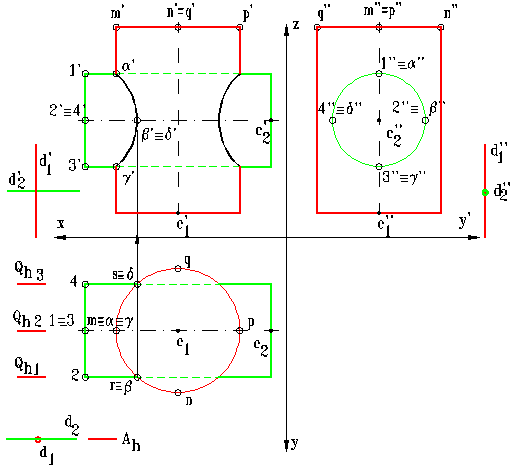 b) Din intersectia
pla-nului [Q2] cu C1 re-zulta generatoarea M iar
din intersectia pla-nului [Q2] cu C2 re-zulta
generatoarele 1 si 3 (generatoarele de contur aparent in plan vertical).
b) Din intersectia
pla-nului [Q2] cu C1 re-zulta generatoarea M iar
din intersectia pla-nului [Q2] cu C2 re-zulta
generatoarele 1 si 3 (generatoarele de contur aparent in plan vertical).
i) Din intersectia ge-neratoarei 1 cu gene-ratoarea M rezulta punctul α (α, α', α'') al curbei de intersectie.
ii) Din intersectia ge-neratoarei 3 cu gene-ratoare M se obtine punctul γ (γ, γ', γ'') al curbei de intersectie.
c) Din intersectia pla-nului [Q3] cu C1 re-zulta generatoarea S iar din intersectia pla-nului [Q3] cu C2 re-zulta generatoarea 4, punctul lor comun fiind δ (δ, δ', δ'').
Fig. 10
Vizibilitatea curbei de intersectie se evalueaza pe baza regulii referitoare la vizibilitatea punctelor apartinand curbelor de pe suprafata respectiva. Astfel:
 - in proiectia
orizontala sunt vizibile punctele ce apartin generatoarelor vi-zibile
δ-α-β ale luiC2
- in proiectia
orizontala sunt vizibile punctele ce apartin generatoarelor vi-zibile
δ-α-β ale luiC2
- in proiectia verticala sunt vizibile α-β-γ pentru ca apartin panzei vizibile a cilindrului C2
- in proiectie laterala sunt vizibile toate punctele curbei pentru ca apartin panzei vizibile a cilindru-lui C1
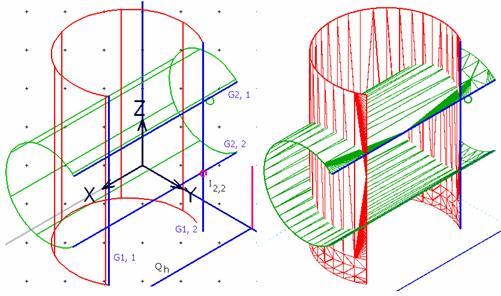
In figura 11 este mode-lata situatia cand planul auxiliar [Q] intersecteaza cilindrii dupa genera-toarele G1,1, G1,2, G2,1, G2,2. Fig. 11
Rezulta astfel 4 puncte ale curbei de intersectie, dintre care este notat doar unul, I 2,2. Notatia sa arata ca este obtinut din intersectia generatoarei 2 a primului cilindru cu generatoarea 2 a celui de-al doilea cilindru.
EXEMPLUL NR. 2
Fie obiectul din figura 12 obtinut prin reuniunea unui cilindru circular drept cu un trunchi de con cu dimensi-unile indicate. Se cere sa se reprezinte corect vede-rea pe planul vertical si sa se construiasca vederea pe planul lateral.
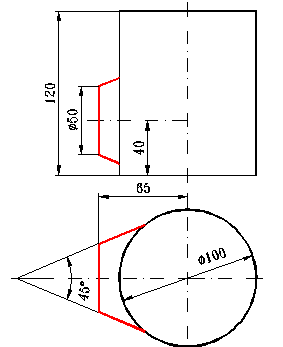 Trebuie rezolvata o
problema de intersectie dintre o suprafata cilindrica
dreapta verticala si o suprafata co-nica
circulara dreapta avand axa o dreapta fronto-orizontala.
Trebuie rezolvata o
problema de intersectie dintre o suprafata cilindrica
dreapta verticala si o suprafata co-nica
circulara dreapta avand axa o dreapta fronto-orizontala.
a) Transpunerea date-lor in epura (figura 13)
Se observa ca:
- s-a construit varful conului si s-a notat S (s, s', s'');
- s-a determinat grafic baza conului (cercul de dia-metru BD);
- s-au notat cu A, B, C, D generatoarele de contur apa ig. 12
rent ale conului;
-s-au notat prin 1, 2, 3, 4 generatoarele de contur aparent ale cilindrului.
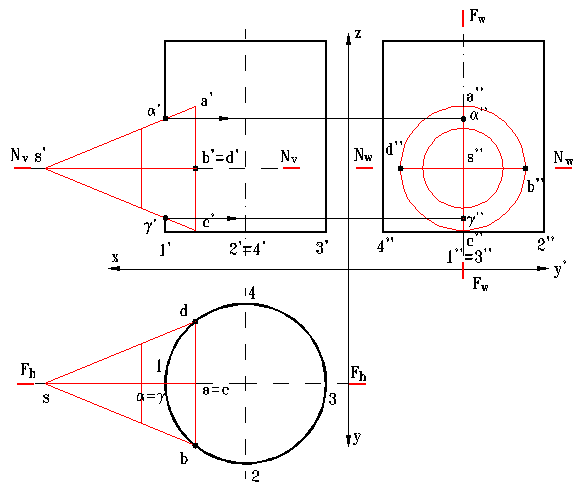
Fig. 13
b) Determinarea punctelor semnificative ale curbei de intersectie (figura 13)
Punctele semnificative ale curbei de intersectie rezulta imediat din intersectia generatoarelor de contur aparent ale celor doua suprafete. Astfel:
- planul de front F contine atat axa cilindrului vertical cat si axa conului, astfel ca generatoarele 1 si respectiv SA si SC sunt coplanare si se intersecteaza, rezultand proiectiile: α' 1' ∩ s'a' si γ' 1' ∩ s'c' ale punctelor α si γ ale curbei din spatiu.
- planul de nivel N care contine axa conului, il sectioneaza dupa generatoarele SB si SD (generatoare de contur aparent in proiectia orizontala) iar sectiunea prin cilindru este un cerc pe care generatoarele SB si SD il intersecteaza in B(b, b', b'') si D(d, d', d''), care sunt alte doua puncte ale curbei spatiale de intersectie.
Fig. 14
c) Determinarea unor puncte suplimentare ale curbei de intersectie (figura 14)
Se construieste un plan auxiliar de
sectiune conform recomandarii specifice rezolvarii
intersectiei dintre o suprafata cilindrica si una
conica, asa cum se arata in figura 14. Pentru a construi planul auxiliar de
sectiune [Q] se parcurg etapele
Fig. 7
de mai jos.
i) Se construieste o dreapta verticala Δ (δ, δ') II 1, avand o pozitie convenabila. Varful S (s, s', s'') si aceasta dreapta determina complet planul [Q].
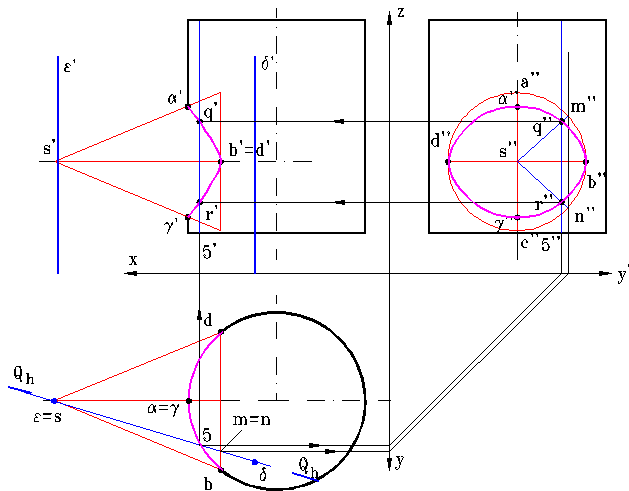 ii) Pentru a trasa urma
orizontala Qh este nevoie de urmele orizontale a doua
drepte continute in plan, deci se mai construieste prin S o a doua
dreapta verticala Ε(ε, ε'). Deoarece Δ si
Ε sunt drepte verticale, urmele lor orizontale se confunda cu
proiectiile orizontale δ si ε, astfel ca acestea
determina Qh.
ii) Pentru a trasa urma
orizontala Qh este nevoie de urmele orizontale a doua
drepte continute in plan, deci se mai construieste prin S o a doua
dreapta verticala Ε(ε, ε'). Deoarece Δ si
Ε sunt drepte verticale, urmele lor orizontale se confunda cu
proiectiile orizontale δ si ε, astfel ca acestea
determina Qh.
Planul [Q] intersecteaza cilindrul vertical dupa generatoarea 5 (5, 5', 5'').
Planul [Q] intersecteaza conul dupa generatoarele SM si SN. Se determina mai intai proiectiile orizon-tale m = n, apoi proiectiile laterale m'' si n'' si se traseaza proiectiile laterale s''m'' si s''n'' ale generatoarelor.
In spatiu generatoarea cilindrului 5 si generatoarele SM si SN ale conului sunt coplanare si se intersecteaza, rezultand punctele curbei de intersectie: Q SM ∩ 5 si R SN∩5. Se determina usor proiectiile lor laterale: q'' s''m'' ∩ 5'' si r'' s''n'' ∩ 5''.
d) Reprezentarea corpului rest (figura 15)
Se traseaza curba de intersectie in proiectia verticala (nu este un arc de cerc sau de elipsa) si se traseaza si proiectia ei laterala, unind proiectiile laterale ale punctelor (figura 15).
In
proiectiea orizontala curba spatiala de intersectie se
proiecteaza deformat ca un arc de cerc deorece 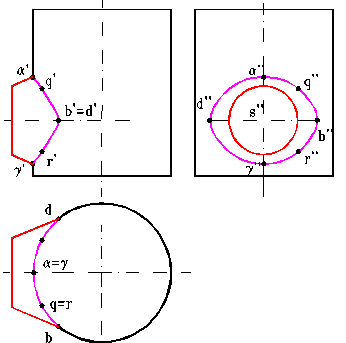 suprafata
cilindrica este suprafata proiectanta fata de
planul orizontal.
suprafata
cilindrica este suprafata proiectanta fata de
planul orizontal.
Fig. 15
Observatii
Modelarea obiectelor (piese, structuri me-talice) cu ajutorul suprafetelor este imposibila fara stapanirea principiilor de rezolvare a acelorasi pro-beme cu ajutorul geometriei descriptive. In figurile 16, 17 si 18 sunt prezentate etapele care se parcurg pentru modelarea tridimensionala a acelu-iasi obiect - o parte dintr-un rezervor.
In figura 16 sunt prezentate punctele ca-racteristice ale suprafetelor cilindrica si conica si determinarea coordonatele lor (necesare pentru modelare).
In figura 17 este prezentat rezultatul modelarii si al determinarii curbei de intersectie. Evident, rezul-tatul este acelasi, dar un utilizator neavizat nu poate intelege cu usurinta curba de intersectie.
In figura 18 este prezentat rezultatul decuparii suprafetei cilindrice de catre suprafata conica si aspectul obiectului rezultat, intr-o maniera mai intuitiva. In cazul in care proiectantul a definit gresit suprafetele sau pozitia lor reciproca, in aceasta etapa finala a modelarii, nu se mai pot corecta greselile si procesul de modelare trebuie reluat.

Fig. 16
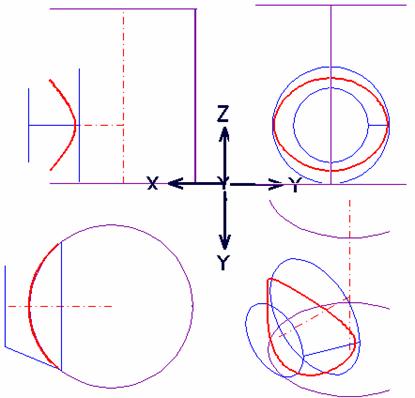
Fig. 17
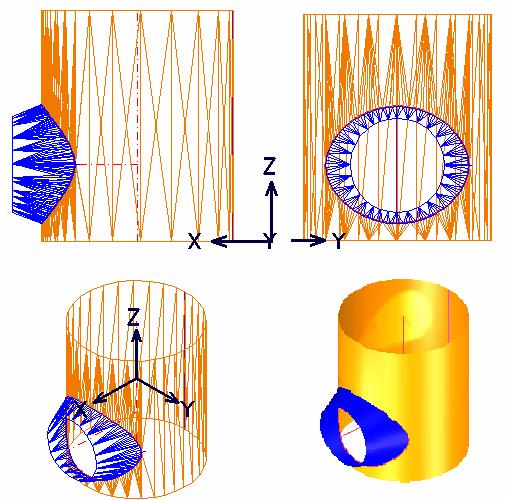
Fig. 18