Controlerul in sistemele mecatronice

CONTROLERUL IN SISTEMELE MECATRONICE

Introducere

In ansamblul sistemului mecatronic, controlerul ocupa un loc important fara de care nu se poate realiza automatizarea procesului pe care il implica existenta sistemului.

Utilizarile practice au evidentiat in timp diverse variante de realizare a unor sisteme prin care un parametru era mentinut in jurul unei valori de referinta. Regulatorul Watt (vezi cursul 1) a deschis aceste realizari.

De exemplu un mod simplu de reglare a nivelului de lichid dintr-un rezervor este prezentat in fig. 1. Nivelul lichidului din rezervor se regleaza prin deschiderea sau inchiderea conductei de golire prin intermediul unui plutitor si a unui mecanism cu parghii.

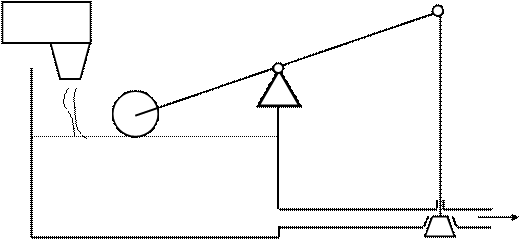
Fig. 1 Schema principiala pentru un sistem simplu de reglare a nivelului

Intr-o varianta simpla si de generalitate extrema "Controlerul", are rolul de a prelucra dupa o anumita lege, eroarea rezultata din comparatia marimii de intrare X si a celei de reactie R:

                                      (1)

si de a furniza la iesire o marime de comanda U care se aplica obiectului reglat (fig. 2).

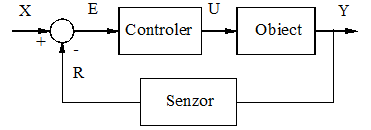
Fig. 2 Schema bloc principiala a unui sistem incluzand un controler si un senzor pe reactie

In absenta elementului de reglare - controler - marimea de iesire ar suporta modificari importante si necontrolate datorita efectelor perturbatoare care actioneaza in diferite puncte ale obiectului avut in vedere.

Sa reconsideram, in concordanta cu cele prezentate anterior, problema reglarii debitului intr-o conducta. Schema principiala este prezentata in fig. 10.3, unde semnificatia notatiilor este urmatoarea:

‑ TR - traductor / senzor = converteste o mǎrime fizicǎ intr-un semnal in general electric;

‑ EE - element de executie (motor electric) a componentei hidraulice.

Prin intermediul traductorului TR se obtine o informatie privind debitul real Q_m in conductǎ, valoare exprimatǎ printr-un semnal in tensiune U_m.

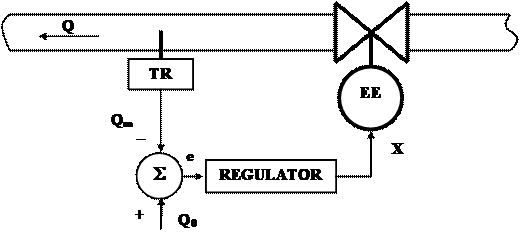
Fig. 3 Schema principiala a unui sistem de regalre a debitului

De exemplu dependenta intrare - iesire a traductorului (debit - tensiune) se obtine printr-o operatie de calibrare si se reprezintǎ prin valorile date in tabel sau grafic:

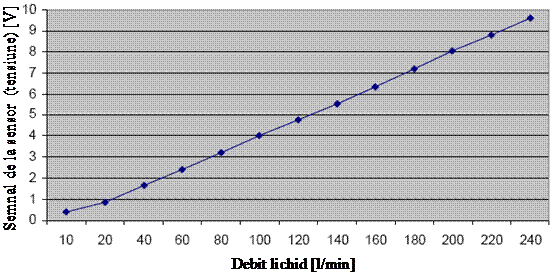
Fig. 4 Dependenta debit - tensiune a traductorului utilizat in sistemul din fig. 3

Din cele douǎ valori, se poate obtine relatia de legǎturǎ debit - tensiune sau sensibilitatea traductorului:

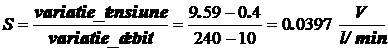(2)

Valoarea obtinuta se comparǎ in elementul de comparatie S cu valoarea impusǎ pentru debitul Q₀, exprimatǎ prin semnalul U₀, rezultatul concretizandu-se prin eroarea:

                                  (3)

Controlerul inclus in cadrul sistemului asigurǎ mǎrimea de intrare X pentru elementul de executie EE care deschide sau inchide robinetul montat pe conductǎ.

O clasificare a controlerelor poate fi realizata dupa diverse criterii:

‑ forma relatiei dintre marimea de comanda si eroare:

controlere continue (marimea de comanda U este influentata in mod continuu de eroarea E),

controlere discrete;

- natura fizica a marimilor de la intrarea si iesirea controlerului:

controlere electrice,

controlere pneumatice,

controlere hidraulice.

- sursa de energie cu care functioneaza:

controlere directe (functioneaza pe baza energiei preluate din proces prin intermediul traductoarelor de reactie),

controlere indirecte (cu sursa de energie auxiliara).

Modelul matematic al controlerului

Controlerele cu actiune continua cu o larga utilitate se disting dupa dependenta de regim dinamic care se stabileste intre marimile U si E (fig. 2):

‑ proportionale (simbol P):

                          (4)

unde K_P este factorul de amplificare al controlerului.

‑ integrale (simbol I):

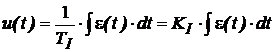                  (5)

unde T_I are dimensiune de timp si se numeste constanta de integrare.

­‑ derivative (simbol D):

                             (6)

unde T_D are dimensiune de timp si poarta denumirea de constanta de timp derivativa.

- combinatii: PI, PD, PID. Varianta PID este cea mai completa care permite performante superioare atat in regim stationar cat si regim dinamic. Relatia de dependenta a controlerului PID poate fi scrisa sub forma:

(7)

Scopul controlerului este de asigura un timp de crestere corespunzator, o supracrestere minima, fara eroare stationara. Modul in care constantele controlerului influenteaza performantele este prezentat calitativ in tab. 1.

Tabelul 1

Aspecte de realizare practicǎ a componentelor din sistemul de reglare

In cazul general, un regulator electronic (controler) continuu poate fi considerat ca avand structura din fig. 5. Acesta se compune dintr-un amplificator operational AO, un circuit pasiv de intrare (1) si un circuit pasiv de reactie (2).

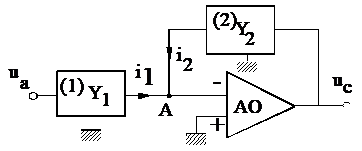
Fig. 5 Structura principiala a unui regulator

Admitantele de transfer ale celor doua circuite pasive se definesc, pe baza notatiilor din fig. 5 prin relatiile:

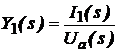                            (8)

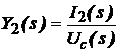                            (9)

Presupunand ca AO este ideal (, punctul A avand potential zero), functia de transfer a acestui circuit se poate defini ca fiind:

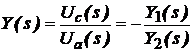(10)

In tab. 2 se prezinta modalitati de realizare a unor tipuri de controlere prin utilizarea amplificatoarelor operationale si in concordantǎ cu cele precizate anterior referitor la functia de transfer.

Tabelul 2

Un bloc component al controlerului este blocul de insumare; acesta indeplineste rolul de a efectua o operatie de adunare sau scadere a unei marimi analogice (tensiune).

Amplificatorul operational poate realiza suma sau diferenta mai multor tensiuni utilizand o schema asemanatoare cu cea din fig. 10.6.

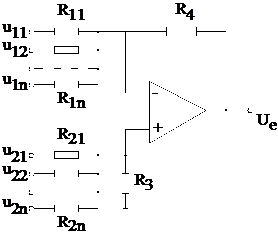
Fig. 6 Schema pentru efectuarea sumei si diferentei mai multor tensiuni foilosind circuite cu amplificator operational

Din motive de micsorare a erorii cu temperatura, este indicat ca R₃ = R₄. Pentru a obtine o insumare cu ponderi egale pentru toti termenii pozitivi si negativi, este necesar ca rezistentele R_1i (i= 1,n) si R_2j (j= 1, m) sa fie egale. Considerand n=m, tensiunea la iesirea amplificatorului operational va fi:

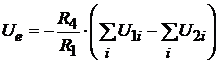                                  (11)

Elementul de comparatie (EC) din schema de reglare are rolul de stabili eroarea existenta intre marimea de referinta si marimea reglata, ajunsa la comparator prin calea de reactie (fig. 7).

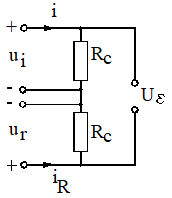
Fig. 7 Element de comparatie realizat prin rezistoare

O posibilitate de realizare fizica a EC are la baza schema din fig. 10.7. Doua rezistente egale R_c sunt strabatute in sensuri opuse de curentii i_R si respectiv i; i_R este proportional cu marimea reglata, iar i este proportional cu marimea de intrare. Marimea de intrare poate fi denumita marime de referinta, sau marime prescrisa, daca are valoare constanta. Tensiunea la iesirea din elementul de comparatie EC se poate exprima prin relatia:

   (12)

si va fi proportionala cu eroarea ε a sistemului de reglare.

Un aspect de realizare practicǎ al controlerului proportional este prezentat in fig. 8 si 9.

Fig. 8 Exemplu practic de controler proportional

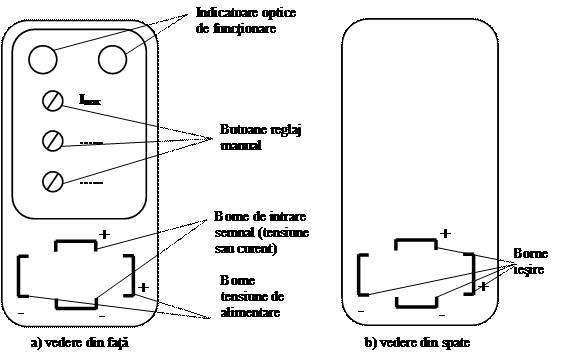Fig. 9

Analiza sistemului de reglare

Un sistem sub forma sa generalǎ si in concordantǎ cu scopul de reglare propus se poate concretiza conform schemei bloc din fig. 10 unde:

‑ X(s) este mǎrimea de intrare (de referintǎ) pentru sistem;

‑ Y(s) este mǎrimea de iesire din sistem;

‑ W_R este functia de transfer a controlerului;

‑ W_E este functia de transfer a eventualului element de executie (dacǎ acest element lipseste, functia de transfer se considerǎ unitarǎ);

‑ W_O este functia de transfer a obiectului / procesului reglat.

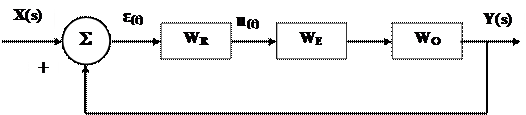
Fig. 10 Schema bloc a unui sistem automat incluzand un controler

Conform algebrei schemelor bloc, functia de transfer a sistemului este:

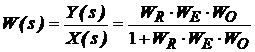                       (13)

Controlerul prin functia sa de transfer trebuie astfel proiectat incat sistemul analizat cu functia de transfer W(s) si orientat de la X(s) spre Y(s), sǎ respecte performantele de calitate.

Se analizeaza aspecte practice si teoretice ale unor variante de controlere.

Controlerul proportional

Consideratii teoretice

Prin ecuatia (4) s‑a prezentat dependenta dintre mǎrimea de iesire a controlerului si eroarea mǎsuratǎ in sistem. Factorul de proportionalitate K_P reprezinta singurul parametru al regulatorului. Prin constructie, acest parametru se prevede a fi ajustabil in limite largi pentru a satisface o mare varietate de legi de reglare.

In mod real, ecuatia controlerului este:

               (14)

unde Du este valoarea zgomot al controlerului. Aceastǎ valoare se poate ajusta manual.

Caracteristica idealǎ si respectiv realǎ a controlerului proportional este prezentatǎ in fig. 11.

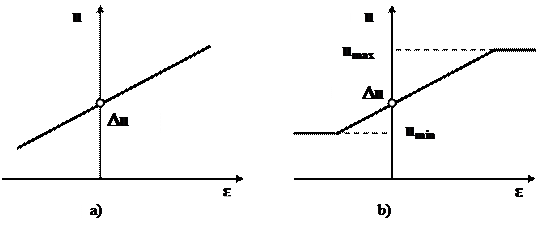
Fig. 11 Caracteristicile ideala (a) si reala ale unui controler proportional

Deseori se utilizeaza in locul factorului K_P factorul denumit banda de proportionalitate BP definita procentual:

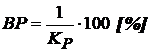                   (15)

Pentru un proces/ obiect reglat de ordinul 1 cu functia de transfer:

                                   (16)

si considerand W_E = 1, functia de transfer a sistemului reglat, conform relatiei (13), este:

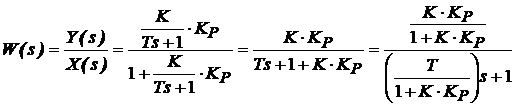
(17)

Functia de transfer (17) a sistemului permite o analizǎ a efectelor introduse de controler asupra performantelor acestuia.

Pentru a afla dacǎ controlerul proportional este adecvat sistemului considerat, se determinǎ modul de evolutie in timp a erorii din sistem:

                                  (18)

sau:

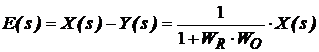     (19)

Pentru sistemul de ordinul 1 considerat se obtine:

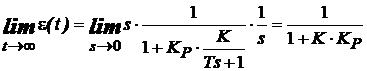(20)

care aratǎ cǎ eroarea tinde spre zero pentru .

Exemplu

Fie sistemul de ordinul 1 cu functia de transfer . Functia de transfer a sistemului reglat din sistem pentru cazul utilizǎrii unui controler proportional este:

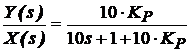                            (21)

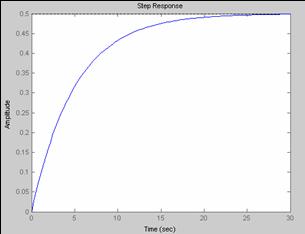
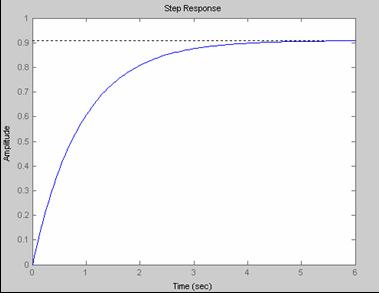
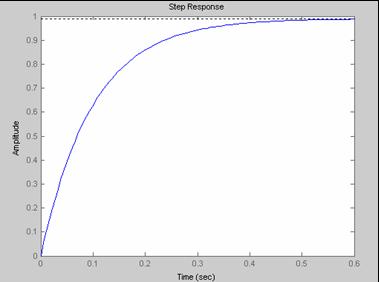
Rǎspunsul sistemului la un semnal de intrare treaptǎ unitar pentru diverse valori ale lui K_P este prezentat in fig. 12 (a - K_P = 0.1, b- K_P = 1, c - K_P = 10).

         a)

b)

c)

Fig. 12 Raspunsul sistemului studiat la semnal treapta unitara pentru diferite valori ale parametrului K_p

Pentru un sistem (obiect reglat) de ordinul 2 se considera functia de transfer:

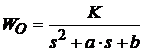                     (21)

pentru care, pe principiul anterior (vezi relatia 13), se obtine functia de transfer a sistemului reglat:

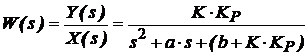        (22)

si pentru care pulsatia si respectiv coeficientul de amortizare au valorile:

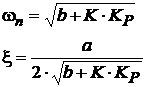                    (23)

Din relatia 23, se observǎ influenta controlerului asupra pulsatiei proprii si respectiv asupra coeficientului de amortizare.

Evolutia in timp a erorii se determinǎ conform relatiei (19):

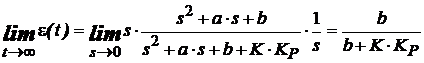(24)

Se considerǎ acum cazul sistemului de ordinul 2 de forma particularǎ:

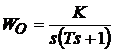                              (25)

pentru care relatia anterioarǎ (24) conduce la:

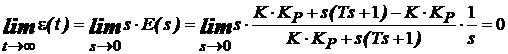
(26)

Acest rezultat se obtine pentru sistemele cu un pol in zero (numitorul contine factorul s).

Exemplu

Sistemul supus problemei de control este format dintr-o masa inertiala "m" aflata sub actiunea fortei "F" si sub actiunea unor legaturi elastice si respectiv de amortizare (fig. 13).

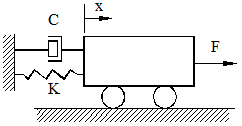
Fig. 13 Sistem de ordinul doi supus unei reglari de tip proportional

Modelul matematic al sistemului este descris de ecuatia:

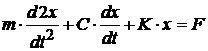   (25)

Acest model permite obtinerea functiei de transfer a sistemului de forma:

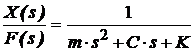(26)

Fie cazul numeric: m = 2 kg, C = 10 Ns/m, K = 25 N / m, F = 2 N

Raspunsul sistemului functionand in circuit deschis la semnal treapta unitara este prezentat in fig. 14, pe baza unei simulari in mediul Matlab (fisierul contr_1.m).

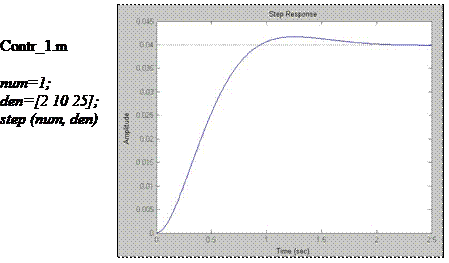
Fig. 14 Raspunsul sistemului de ordinul doi analizat in circuit deschis la semnal treapta unitara

Analiza raspunsului evidentiaza o amplificare 1/25, existenta unei supracresteri si atingerea valorii de regim stationar dupa un timp de 2 s s.a.m.d.

Se urmareste proiectarea unui controler proportional care sa amerioleze performantele sistemului.

Functia de transfer a sistemului reglat (conform celor specificate anterior) este:

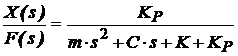                            (27)

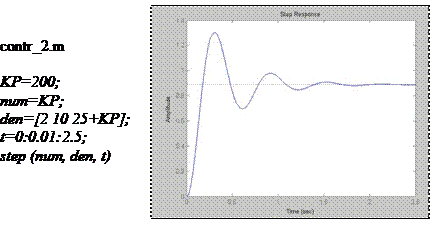
Fig. 15 Raspunsul sistemului de ordinul doi analizat in circuit inchis, cu regulator proportional, la semnal treapta unitara, pentru parametrul K_p=200

Analiza raspunsului sistemului in circuit inchis confirma influentele calitative datorate controlerului proportional (tab. 1): timpul de crestere scade dar creste suprareglarea.

Pentru un K_P = 1000 se obtine raspunsul din fig. 16.

Fig. 16 Raspunsul sistemului de ordinul doi analizat in circuit inchis cu regulator proportional, la semnal treapta unitara, pentru parametrul K_p=1000

Fisierul - m de rezolvare a simularii poate fi creat in jurul functiei Matlab denumite cloop care permite obtinerea functiei de transfer pentru sistemul in circuit inchis pornind de la functia sistemului in circuit deschis (fig. 17).

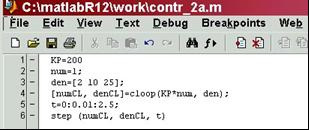
Fig. 17 Simularea sistemului inchis in Matlab, prin functia cloop

Exemplu

Fie procesul de reglat prin controler proportional cu functia de transfer (28). Rǎspunsurile sistemului reglat pentru K_P: 0.01, 0.1, 1 sunt redate in fig. 18.

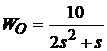                        (28)

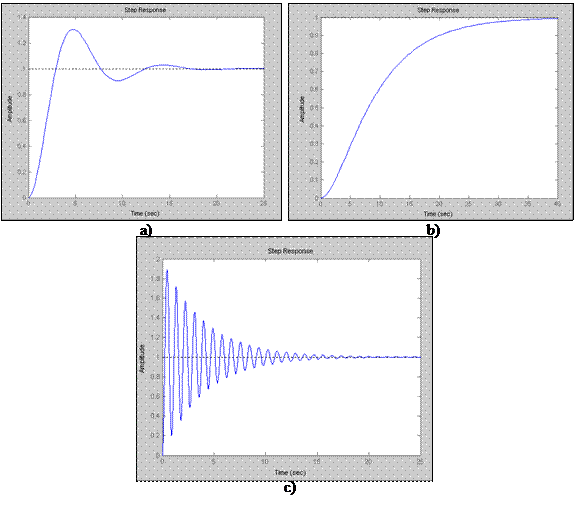Fig. 18 Raspunsul sistemului de ordinul doi (28) analizat in circuit inchis cu regulator proportional la semnal treapta unitara pentru parametrul K_p de diferite valori

In acelasi mod se analizeazǎ variantele de controlere PI, PD, PID.

Controlerul PID

Consideratii teoretice

Aplicand transformata Laplace, ecuatia de rǎspuns (7) a controlerului PID devine:

(29)

sau:

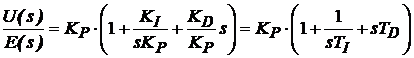(30)

Schematic, controlerul PID este prezentat in fig. 19.

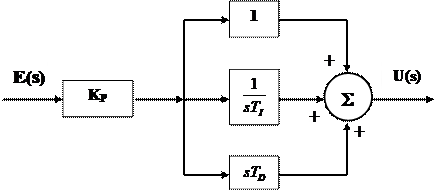
Fig. 19 Schema bloc a controlerului de tip PID

Proiectarea - determinarea valorilor parametrilor controlerului PID - presupune o optimizare pe diverse criterii de performantǎ:

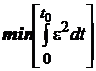 - integrala erorilor pǎtratice (31)

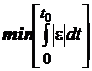- integrala erorilor absolute                   (32)

O alternativǎ de proiectare este considerarea conditiei de existentǎ a unui raport B/A=0.25 intre primele douǎ valori extreme ale semnalului de rǎspuns al sistemului reglat (fig.20).

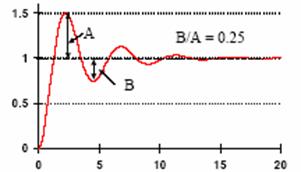
Fig. 20 Raspunsul sistemului reglat incluzand un controler de tip PID

Determinarea parametrilor corespunzǎtori controlerului PID este in general un proces complex.

Metoda Ziegler - Nicholls considerǎ urmǎtoarea procedurǎ pentru ajustarea parametrilor:

1.     minimizarea actiunilor I si D;

2.     determinarea valoriii K_P pentru care existǎ un rǎspuns oscilator constant;

3.     se considerǎ valoarea amplificǎrii pentru acest caz K_U;

4.     se noteazǎ perioada de oscilatie completǎ T_U;

5.     se determinǎ valorile parametrilor pe baza relatiilor din tab.3.

Tabelul 3

O metodǎ de real ajutor este simularea functionǎrii sistemului.

Exemplu

Sǎ reconsiderǎm sistemul format din element in miscare de translatie (fig. 13). Functia de transfer a sistemului cu utilizarea unui controler PID este in acest caz definita de ecuatia:

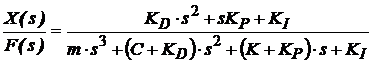(33)

iar rezultatul simularii este prezentat in fig. 21. Se constata ca cerintele de pornire referitoare la parametrii impusi au fost atinse, raspunsul sistemului apropiindu-se de un semnal treapta.

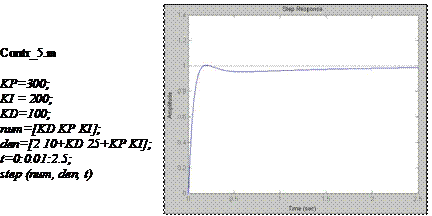
Fig. 21

Concluzii

Ca o concluzie finalǎ se prezintǎ rǎspunsul calitativ al unui sistem functie de tipul regulatorului folosit.

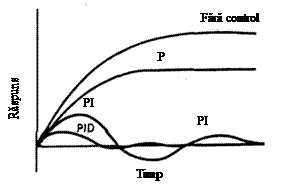
Fig. 10.22 Rǎspunsul calitativ al unui sistem in functie de tipul controlerului folosit