Ipotezele de baza din rezistenta materialelor

Ipotezele de baza din rezistenta materialelor

1. Generalitati.

Sarcina rezistentei materialelor consta in studierea fortelor interioare si elaborarea de metode cat mai simple si rapide , pentru calculele de rezistenta . Fortele interioare care apar in corpurile deformabile sunt in functie de marimea si distributia sarcinilor exterioare . In constructia de masini si in constructia structurilor se utilizeaza o mare varietate de materiale : metalice , polimeri, ceramice, compozite, etc.

Comportarea diverselor materiale supuse la acelas sistem de forte exterioare este diferita . Pentru calculul fortelor interioare se foloseste instrumentul matematic clasic care in mod implicit conduce la o serie de ipoteze simplificatoare , in conditiile de valabilitate in raport cu rezultatele experimentale.

Ipoteza continuitatii materiei.

La scara macromecanica , materia poate fi cosiderata continua si nu discreta cum este in realitate ( formata din atomi si molecule ). Aceasta ipoteza permite lucrul cu functii continui , trecerea la limita , inlaturand marile dificultati de calcul intalnite in fizica corpului solid.

3. Ipoteza omogenitatii materiei.

Materialul este considerat omogen , avand aceleasi proprietati fizico-chimice in tot volumul sau . In realitate , din cauza structurii sale granulare sau moleculare , un material nu poate fi omogen in sensul aratat mai sus , dar la constructiile metalice si structuri care au dimensiuni incomparabil mai mari decat distantele interatomice , particularitatile lor sunt neesentiale.

4. Ipoteza mediului izotrop.

Materialul este considerat izotrop (caracteristicele elastice si mecanice sunt aceleasi in toate directiile) .

5. Ipoteza elasticitatii materialului.

Materialul studiat este considerat perfect elastic , adica revine la forma si dimensiunile initiale dupa inlaturarea sarcinilor, in realitate cand se depasesc anumite limite ale sarcinilor aceasta ipoteza nu mai este valabila. Este valabila cand materialele lucreaza sub limita de elasticitate.

6. Ipoteza deformatiilor mici.

Experimental se considera ca deformatiile elastice sunt foarte mici in raport cu dimensiunile corpurilor. In cadrul acestei ipoteze se adopta principiul geometriei si dimensiunilor initiale ale corpului sau sistemului.

Exemplu

In primul caz din figura 33 , avem in nodul Q de aflat fortele care actioneaza si, care se afla din conditiile de echilibru 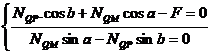_; de unde rezulta

si

S-a adoptat principiului geometriei si a dimensiunilor initiale ale sistemului . Daca nu se adopta acest principiu avem cazul din figura 35 unde in nodul Q^" avem ca necunoscute fortele si unghiurile a^',b^' exista in acest caz patru necunoscute si numai doua ecuatii , se obtine o problema dublu static nedeterminata :

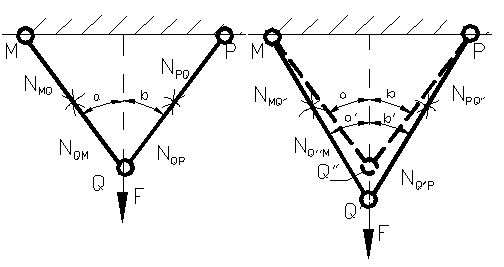
Figura 33

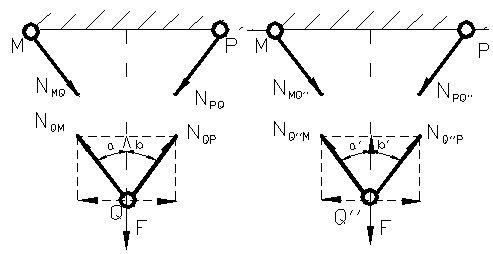
Figura 34 Figura 35

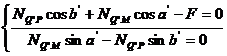. Acest principiu nu se aplica in cazul sistemelor daca se schimba forma sistemului in mod sensibil sub actiunea sarcinilor.

Exemplu:

In cazul din figura 36 trebuie sa tinem cont si de unghiurile a si b pentru ca se modifica foarte mult forma sistemului, se abate de la geometria initiala destul de accentuat.

Ipotezele de baza ale rezistentei materialelor simplifica mult calculul din probleme si din teoremele de baza .

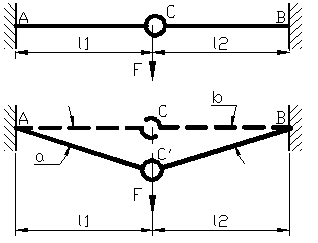
Figura 36

7. Ipoteza proportionalitatii intre tensiuni si deformatii.

Daca solicitarea corpului este de o asa maniera incat materialul ramane in domeniul elastic, se presupune ca intre tensiuni si deformatii exista o dependenta liniara, exprimata prin legea lui Hooke ( σ =E.ε si τ =G.γ ).

8. Principiul lui Saint-Venant.

Daca un sistem de forte este inlocuit cu un alt sistem static echivalent , acesta produce diferente apreciabile in starea de tensiuni si deformatii din vecinatatea fortelor dar ramane fara efect , sau cu efecte neglijabile , la distante suficient de mari de locul de aplicatie al fortelor. Aceasta inlocuire cu dR a fortelor distribuite nu produc modificari in starea de tensiuni si deformatii din sectiunea A-A din figura 37 sau forta R din sectiunea B-B din figura 38 , aflata la o distanta ( l ) suficient de mare.

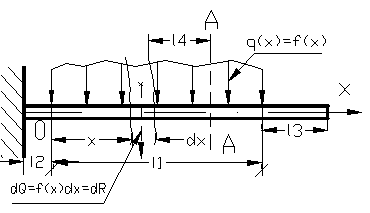
Figura 37

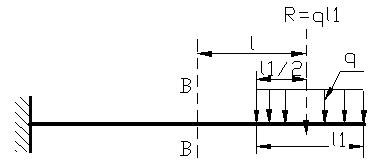
Figura 38

9. Ipoteza starii normale.

Aceasta presupune ca in corpurile solide nu exista tensiuni in lipsa sarcinilor. Admitand aceasta ipoteza , se poate demonstra teorema lui Kirchoff care spune ca pentru un corp , cu o rezemare si un sistem de forte date , starea de tensiuni si deformatii este mica . Dar in realitate cand se fac unele structuri trec prin unele procese tehnologice complexe ( sudare, nituire, forjare , etc. ) care in mod implicit produc tensiuni si deformatii remanente .

10. Ipoteza lui Bernoulli ( ipoteza sectiunilor plane )

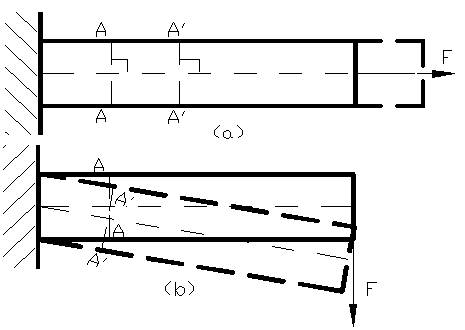
Figura 39

Ipoteza sectiunilor plane este admisa in rezistenta materialelor dar nu si in teoria elasticitatii.

Aceasta ipoteza prevede ca o sectiune plana si perpendiculara pe axa geometrica a grinzii, inainte de deformare, ramane plana si normala pe axa deformata si dupa deformare.

Figura 39 (a) pentru solicitarea la intindere , sectiunea transversala

A-A se deplaseaza paralel cu ea in pozitia A^'-A^' .La solicitarea de incovoiere se observa din figura 39 (b).

Comportarea materialelor la incercari mecanice.

11. Diagramele caracteristice ale materialelor.

11.1. Curba caracteristica la tractiune.

Legea lui Hooke s-a obtinut pe cale experimentala, pe baza incercarilor la tractiune efectuate asupra cablurilor si a otelurilor.

Se incearca o epruveta normalizata conform SR EN 10002-1:1995 .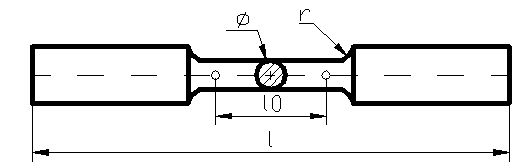

Figura 40

Epruveta este supusa la tractiune cu ajutorul unei masini, ce trage de capetele ei cu doua forte , avand sensul ca in figura 41 .

Epruveta este incarcata cu o forta care creste in mod continu pana la ruperea ei.

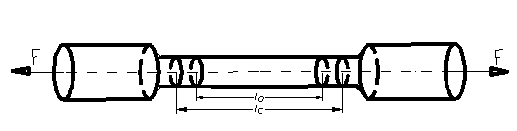
Figura 41

11.1. Diagrama caracteristica

Avem variatia fortei axiale functie de deplasarea falcii masinii, pe diagrama avem urmatoarele regiuni si puncte caracteristice:

0-1 - este zona liniara , numita si zona de proportionalitate (deformatiile sunt proportionale cu fortele )

0-2           - zona de elasticitate in care materialul ramane elastic.

Daca din punctul 2 se produce descarcarea masinii se revine la punctul    0 tot pe 2-1-0, nu sunt deformatii permanente (plastice).

Din punctul 2 in 3 alungirile nu mai sunt nici proportionale , nici elastice, cu alte cuvinte ne aflam in domeniul deformatiilor permanente.

Zona 3-4, zona de curgere , unde forta se mentine aproximativ constanta dar creste mult deformatia.

Punctului 3 ii corespunde forta de curgere F_c si deformatia de curgere dl_c.

Zona 4-5 in care forta creste in continuare, ca urmare a ecruisarii materialului.

Zona 5-6 , este zona de cedare , in care forta scade ca urmare a micsorarii sectiunii epruvetei, dupa aparitia zonei de strictionare.

In punctul 6 , epruveta se rupe. Daca in punctul B epruveta se descarca, se obtine o deformatie remanenta si apoi se incarca epruveta , observam ca s-a marit limita de elasticitate. Tensiunea normala R = unde = iar ε = deformatia specifica, in sistemul de coordonate si ε obtinem curbele caracteristice

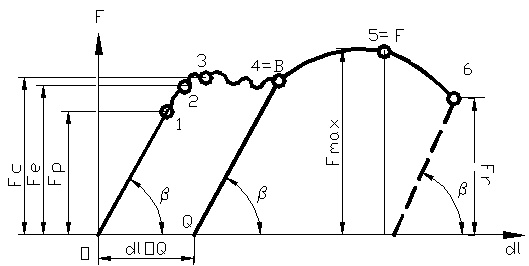
Figura 42

2.11.2        Curba caracteristica la intindere pentru un otel

In general curba caracteristica prezinta o portiune liniara OA in care lungirea epruvetei este proportionala cu forta aplicata, in aceasta zona este valabila legea lui Hooke = ε.E ( fig.43). Tensiunea corespunzatoare punctului A se numeste limita de proportionalitate, urmatorul punct al curbei caracteristice este punctul B numit limita de elasticitate.

Dupa depasirea acestui punct, materialul capata deformatii remanente, zona deformatiilor plastice permanente poate avea aspecte diferite, in functie de natura materialului .

Raportul dintre forta la care apare curgerea si aria sectiunii initiale se numeste limita de curgere aparenta R_C. Daca in timpul curgerii sarcina variaza, se determina limita de curgere superioara si limita de curgere inferioara ( R_eh, R_el). In materialele la care apare fenomenul curgerii fara palierul de curgere, stabilirea limitei de curgere R_0,2 se face conventional ca in figura 44. Se definesc urmatoarele caracteristici

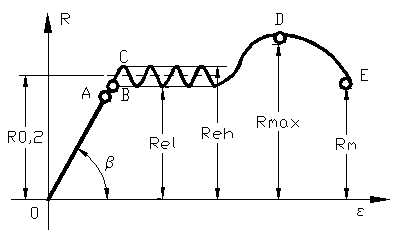
Figura 43

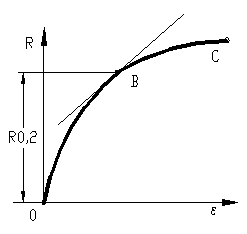
Figura 44

- limita de curgere conventionala R_c= R_0,2 sau R_p , se defineste ca raportul dintre sarcina corespunzatoare unei alungiri neproportionale prescrise si aria sectiunii transversale a epruvetei ; uzual, pentru oteluri se prescrie o alungire de 0,2% limita notata cu R_0,2;

-limita de curgere remanenta R_r , ca raportul dintre sarcina corespunzatoare unei alungiri remanente si aria sectiunii transversale a epruvetei ; de obicei se prescrie alungirea remanenta de 0,2% , limita notata cu R_r0,

11.3. Curba caracteristica a otelului la compresiune.

Pentru otelurile moi se poate construi curba caracteristica la compresiune, pentru incercari se folosesc epruvete cilindrice ce au dimensiunile urmatoare: h = d ( 10-30 ) mm.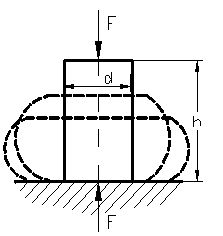

Figura 45

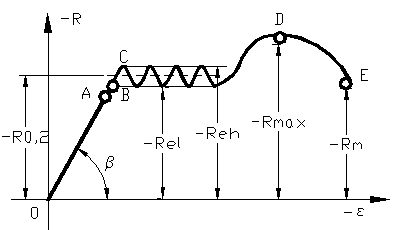
Figura 46

Curba caracteristica la compresiune ne arata ca pentru otelurile tenace, caracteristicile mecanice: R_p, R_c , R_e sunt egale in valoare absoluta cu cele de la solicitarea de intindere.

11.4. Curba caracteristica la torsiune.

Supunand la incercarea de torsiune o epruveta cilindrica, confectionata dintr-un otel moale si calculand tensiunile tangentiale si lunecarile specifice se obtine o curba caracteristica asemanatoare celei de tractiune. Pentru zona OA avem unde este valabila legea lui Hooke.

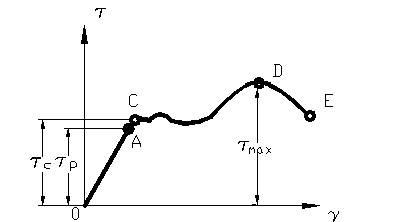
Figura 47

11.5. Curbele caracteristice pentru materialele care nu asculta de legea lui Hooke.

Materialele care nu asculta de legea lui Hooke sunt: metale neferoase, betonul, pietrele, materialele de origine animala si vegetala, pielea, cauciucul, fibrele textile precum si materialele plastice, fibrele artificiale.

Pentru aceste materiale exista relatia : =E₀.ε unde E₀ este modulul de elasticitate mediu longitudinal . E=tg

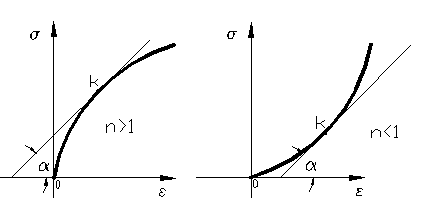
Figura 48

1 Factorii care influienteaza caracteristicile mecanice si elastice ale materialelor.

Variatia caracteristicilor mecanice si elastice este produsa de temperatura, timp si ecruisare. Variatia caracteristicilor mecanice functie de temperatura este prezentata in figura 49 . Pentru un otel cu = 400 N/mm² la temperatura de 20⁰ C din figura 49 , se observa variatia lui . La temperatura de 270⁰ C , = 490 N/mm² , apoi descreste mereu odata cu cresterea temperaturii, ca atare la temperatura de T=800⁰ C, = 60 N/mm² . Iar variatia lui a alungirii specifice se produce invers , valoarea minima a alungirii specifice este in jurul temperaturii de 270⁰ C si maxima a lui in jurul temperaturii de 800⁰ C. Acest lucru se explica pe seama unei anumite durificari capatate de otel la aceasta temperatura , numita zona de fragilizare la albastru . In schimb limita de curgere (T) si limita de proportionalitate (T) si modulul de elasticitate longitudinal, E(T) scad mereu odata cu cresterea temperaturii

( figura 49 ).

O mare influienta in modificarea caracteristicilor mecanice o au si tratamentele termice si anume:

-calirea mareste duritatea , la fel si fragilitatea.

-revenirea pastreaza duritatea si micsoreaza fragilitatea.

-recoacerea anuleaza efectele calirii.

Un alt factor important este timpul in modificarea caracteristicilor mecanice ; variatia tensiunilor si deformatiilor in timp si la temperatura ridicata poarta denumirea de fluaj.

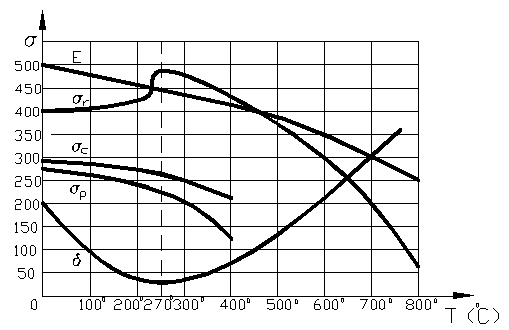
Figura 49

Exemplu:

O epruveta de otel supusa la intindere de catre o forta constanta

( = ct ) si este mentinuta intr-un cuptor electric la temperatura ridicata si constanta ( T=ct ) timp indelungat , se observa ca alungirile cresc cu timpul ca in figura 50 dupa curba de deformatie sub sarcina

constanta.

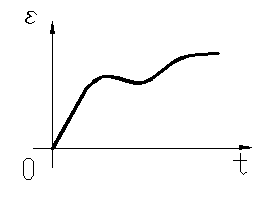
Figura 50

Fenomenul invers, adica se mentine o lungime constanta timp indelungat , o epruveta intinsa si incalzita, se observa ca tensiunile din

ea scad cu timpul.

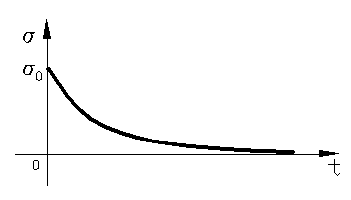
Figura 51

S-a obtinut fenomenul de relaxare a tensiunilor.

2.13.      Teoreme si metode energetice. Energia potentiala de deformatie.

Sub actiunea sarcinilor corpul se defomeaza si punctele de aplicatie ale fortelor exterioare se deplaseaza, implica efectuarea unui lucru mecanic exterior. Pana la limita de elasticitate , lucru mecanic cheltuit pentru deformarea corpului nu se pierde ci se imagazineaza in corpul solid deformat sub forma de energie potentiala de deformatie L = W . S-a studiat ca pentru fiecare material in parte se poate trasa curba caracteristica si ε ( sau τ si γ ) .W_s = L_s= 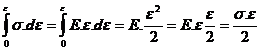. Studiind unitatea de masura a produsului ( ε ) obtinem ceea ce reprezinta lucrul mecanic pe unitatea de volum. Lucrul mecanic total se obtine prin integrare a lucrului mecanic infinitezimal specific de deformatie: dW = Ls ; ; ; W = L= unde dV= dx.dy.dz

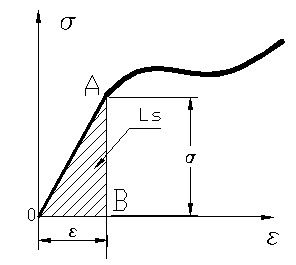
Figura 52

Figura 53

Pentru solicitarile in care avem in mod analog L=;

L_s =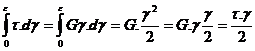 =L_s se numeste energie potentiala de deformatie specifica din fig.54 .

L= , deci s-a pornit de la lucrul mecanic pe unitatea de volum si prin integrare se obtine lucrul mecanic total.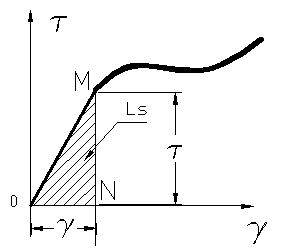

Figura 54