
|
|
|
Puteri cu exponent real pozitiv
Fie ![]() un
numar real pozitiv si
un
numar real pozitiv si ![]() sirurile aproximarilor
zecimale de ordinul n prin lipsa,
respective prin adios ale numarului real x.
sirurile aproximarilor
zecimale de ordinul n prin lipsa,
respective prin adios ale numarului real x.
Atunci,
pentru orice numar natural n au loc relatiile:![]()
Pentru
orice ![]() au loc inegalitatile:
au loc inegalitatile:
![]() , daca a > 1 ;
, daca a > 1 ; ![]() , daca 0 < a < 1
, daca 0 < a < 1
![]() Fie
a si x
numere reale positive. Puterea cu exponent real pozitiv x a
numarului pozitiv a este numarul real y care, pentru orice
Fie
a si x
numere reale positive. Puterea cu exponent real pozitiv x a
numarului pozitiv a este numarul real y care, pentru orice ![]() , verifica inegalitatile:
, verifica inegalitatile:
![]() , daca a > 1;
, daca a > 1;
![]() , daca 0 < a < 1
, daca 0 < a < 1
Puteri cu exponent real negativ
Daca
a > 0este un
numar real si ![]() este un numar real
negativ atunci, prin definitie, puterea
cu exponent real negativ x a numarului pozitiv a este numarul real
este un numar real
negativ atunci, prin definitie, puterea
cu exponent real negativ x a numarului pozitiv a este numarul real 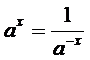
![]()
1.
![]() 2.
2. ![]()
3.
![]() 4.
4. ![]()
5.
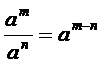 6.
6. ![]()
7.
![]() 8.
8. 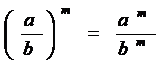
9. ![]() ,
, ![]() 10.
10. ![]()
![]()