Extreme conditionate. Metoda multiplicatorilor lui Lagrange.

Extreme conditionate. Metoda multiplicatorilor lui Lagrange.

Am analizat, pana acum, problema determinarii punctelor de extreme ale functiilor de clasa C¹, cand aceste puncte sunt interioare multimii de definitie a functiei.

In practica, apare insa si situatia determinarii uoor pouncte de extreme ale functiei,pe enumite submultimi ale multimii de definitie, aceste puncte nemaifiind interioare submultimii respective.

In acest sens, sa analizam urmatoarea problema care intervine frecvent in practica:

Sa presupunem ca D este un deschis din RⁿR^m (n≥1,m≥1), f:DR si g:DR^m (sau, echivalent, g=(g₁,g₂,.,g_m) sunt functii de clasa C¹ pe D ).

Am dori sa detreminam punctele de extreme ale functiei f supuse la conditia suplimentara

(8)g(x,y)=0

sau echivalent,

(8')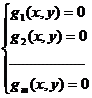

Unde x=(x₁,x₂,.x_n)Rⁿ si y=(y₁,y₂,.,y_m)R^m.

Notand cu A= si tinand seama ca g sete continua (g este de claca C¹ pe D), rezulta ca A este inchisa.

Prin urmare, in problema de mai sus se cere, in fond, determinarea punctelor de extreme ale restrictiei functiei f la multimea A. Observam ca, in general, metoda prezentata pana acum nu poate fi utilizata in acest caz, intrucat punctele lui A vor fin interioare lui A daca si numai daca g este identic nula, situatie nesemnificativa in practica.

Sa vedem cum s-ar putea rezolva totusi problema enuntata.

Observam ca daac am putea rezolva ecuatia (8) in raport cu y , scotand y=, atunci am putea introduce aceasta functie in f, obtinand f(x,) functie de xRⁿ,iar pentru aceasta functie, definite pe o submultime din Rⁿ,am putea studia punctele de extreme prin procedeele cunoscute.

Procedeul acesta este insa greu de aplicat in practica, intrcat, in general, ecuatia (8) nu poate fi rezolvata in raport cu x si chiar daca theoretic se poate rezolva , de cele mai multe ori este freu de pus in evidenta forma explicita a fucntiei.

In continuare, vom cauta sa prezentam o metoda, numita metoda multiplicatorilor lui Lagrange, pentru rezolvarea problemei anuntate, metoda care se aplica, in special, in cazul in care nu poate fi gasita, im mod explicit, forma functiei

Metoda aceasta consta , in realitate, in a asocial functiei f o functie convenabila, nimita functia lui Lagrange, careia sa I se poata determina punctele de xetrem prin metodele deja cunoscute,astfel incat punctele de extreme ale resctrictiei functiei f la A sa poata fi gasite cu ajutorul punctelor obisnuite de extreme pentru funtia asociata.

Pentru a raspunde la aceasta problema, sa dam , mai intai, urmatoarel;e definitii:

Definitia1

Spunem ca un punct (x₀,y₀) este punct de extreme local al functiei f cu restriuctiile (8) sau punct de extrem local conditionat, daca exista o vecinatate V D a punctului (x₀,y₀) a.i. f(x,y)-f(x₀,y₀) sa pastreze semn constant pentru si anume: daca f(x,y)-f(x₀,y₀)≥0, , vom spune ca (x₀,y₀) este punct de minim conditionat, iar daca f(x,y)-f(x₀,y₀)≤0, , vom spune ca (x₀,y₀) este punct de maxim conditionat.

Cu alte cuvinte, spunem ca punctual (x₀,y₀)este punct de extreme conditionat pentru functia f daca (x₀,y₀) este punct de extreme pentru restrictia functiei f la multimea A.

Definitia2

Spunem ca un punct (x₀,y₀) este punct stationar conditionat sau punct critic conditionat al functiei f daca (x₀,y₀) este un punct stationar al restrictiei fucntiei f la multimea A.

In continuare, vom pune in evidenta conditii necesare pentru ca un punct sa fie punct de extrem local conditionat.

Teorema1 (Existenta multiplicatorilor lui Lagrange)

Fie D u deschis din RⁿR^m, f:DR si g:DR^m, adica g=(g₁,.,g_m)cu g_i:DR (i=) functii de clasa C¹ pe D, iar (x₀,y₀) un punct de extrem local al lui f cu restrictia (8) .Daca

(9) ,

Atunci exista m numere reale a.i. daca se considera functia

(10) L=f+

punctul (x₀,y₀) sa verifice sistemul de ecuatii:

(11)

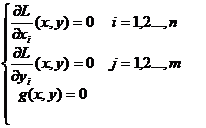
Adica (x₀,y₀) sa fie punct critic al functiei L.

Dem.

Fie functia F(x)=f(x,

Cum (x₀,y₀) este punct de extrem local cu restrictiile (8) pentru f iar (x, , rezulta ca punctul x₀ este punct de extreme local, neconditionat, pentru F pe U.

Tinand seama de teorema lui Fermat (11.6.4), rezulta ca

, i=1,2.,n,

Ceea ce antreneaza

(13)

Intrucat , rezulta ca sistemul liniar

(14) , j=1,2,.,m

Are solutie unica .sa notam aceasta solutie cu Sa artam acum ca pentru functia L=f+sunt indeplinite conditiile (11).

Cum (x₀,y₀) rezulta ca g_k(x₀,y₀)=0, pentru orice k=1,2.,m.

Sa calculam derivatele partiale ale lui L in raport cu x_i.

Avem

Tinand seama de (12), obtinem

=

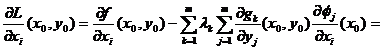
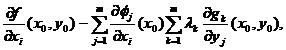
De unde, cum () este solutia sistemului (14), rezulta ca

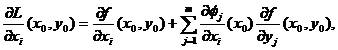
Ceea ce antreneaza conform cu (13) ca

, i=1,2.,n.

Pe de alta parte , derivand in raport cu y_j si tinand seama din nou , ca () este solutia sistemului (14) obtinem:

Prin urmare, conditiile (11) fiind satisfacute, teorema este complet demonstrata.

Observatii!

1. Numerele reale obtinute in teorema precedenta se numesc multiplicatorii lui Lagrange.

2. Punctele de extreme ale functiei f cu restrictiile (8) se gasesc printer punctele critice conditionate ale functiei f, adica printer punctele critice ale functiei associate L=f+

Prin urmare, orice punct de extreme conditionat este un punct critic conditionat al functiei f.Reciproca acestei afirmatii nu este adevarata, intrucat exista puncte critice conditionate care nu sunt puncte de extreme conditionat.

Cu alte cuvinte, conditia ca uin punct sa fie punct critic conditionat este o conditie necesara nu insa si suficienta pentru ca punctual respective sa fie punct de extrem conditionat.

3. Daca in formula (10) presupunem ca si sunt variabile, atunci functia (x,y, L(x,y, DR^m, poarta numele de Lagrangian sau functia lui Lagrange.

4. In practica, pentru determinarea punctelor critice conditionate se procedeaza astfel: se asociaza functia lui Lagrange L=f+ pe DR^m, se anuleaza toate derivatele partiale ale lui L, in numar de n+2m, si se rezolva sistemul astfel format in necunoscutele x₁,x₂,.,x_n,y₁,y₂,.,y_m ,.Orice solutie a sistemului conduce la un punct stationar ()pentru f, iar corespunzatori sunt multiplicatorii lui Lagrange.

Ex4.

Fie functia f(x,y)=cos(x+y) , R².Sa se determine eventualele puncte de extreme al eacestei functii cu conditia x²+y²=1.In acest caz, g(x,y)=x²+y²-1, R².

Fie functia L(x,y)=cos(x+y)+(x²+y²-1).Observam ca

Sa rezolvam sistemul:

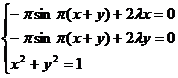
Daca , atunci sin si deci x+y este un intreg.Intrucat x²+y²=1 singurele posibilitati sunt (x,y)=(), (x,y)=( ), pentru care x+y=0 si f(x,y)=1 sau (x,y)=(0,), (x,y)=() , pentru care x+y=si f(x,y)=-1.Daca , atunci x=Cum x²+y²=1, rezulta ca y=.Pentru (x,y)= () si (x,y)= (),f(x,y)=cos.Deci -1<f(x,y)<1.Prin urmare, punctele stationare sunt ( ), (0,

Deocamdata nu am stability conditii sufuciente care sa asigure ca unele dintre aceste puncte sunt de extremum.

Totusi, tinand seama de valorile lui f, vom putea spune ca punctele ( ) sunt puncte de maxim iar punctele de forma (0,) sau () sunt puncte de minim.

In continuare, vom pune in evidenta conditii suficiente pentru ca un punct stationar conditionat (x₀,y₀) sa fie punct de extreme conditionat

Pentru aceasta este normal sa cercetam semnul diferentei

(15) f(x,y)-f(x₀,y₀)

Pentru punctele (x,y) ce verifica (8).

Daca sunt multiplicatoriii lui Lagrange, atunci a cerceta semnul diferentei (15) este echivalent cu a cerceta semnul diferentei L(x,y)-L(x₀,y₀) intrucat

(16) f(x,y)-f(x₀,y₀)=L(x,y)-L(x₀,y₀),

Vom presupune, in continuare , ca f,gC²(D). Aplicand formula lui Taylor functiei L cu restul de ordin 2 si tinand seama ca dL(x₀,y₀)=0 avem

L(x,y)-L(x₀,y₀)=

=

Rationand exact la fel ca in demonstratia teoremei 11.6.8, se vede ca semnul diferentei L(x,y)-L(x₀,y₀) este dat de semnul formei patratice d²L(x₀,y₀).

Intrucat variabilele x₁,x₂,.,x_n, y₁,y₂,.,y_m nu sunt independente (satisfac conditiile (8)), rezulta ca nici diferentialele dx_i, dy_k, i=1,2,.,n, y₁,y₂,.,y_m nu sunt independente, deci vom putea determina dy_k (k=) in functie de dx_i (i=

In adevar, diferntiind sistemul (8') obtinem

+++

.+.+

.+.

Cum , utilizand regula lui Cramer, putem determina dy₁,.,dy_m in functie de dx₁,.,dx_n , care inlocuiti in d²L(x₀,y₀) ne vor conduce la o forma patratica d²L(x₀,y₀)=.

Aplicand aceleasi consideratii algebrice pe care le-am utilizat in demonstratia teoremei 11.6.10, obtinem urmatoarele rezultate:

I. Daca toti determinantii

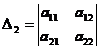
Sunt pozitivi, atunci forma patratica d²L(x₀,y₀) este pozitiv definite , deci f(x,y)-f(x₀,y₀)≥0 pentru , unde V este o vecinatate a punctului (x₀,y₀) .

In acest caz , (x₀,y₀) este punct de minim conditionat.

II. Daca este indeplinita conditia

(-1)^k>0,

Atunci forma patratica d²L(x₀,y₀) este negative definita,

f(x,y)-f(x₀,y₀)≤0 ,

si (x₀,y₀) este punct de maxim local conditionat.

Metoda de mai sus, utilizata pentru determinarea punctelor de extreme conditionat se numeste metoda multiplicatorilor lui Lagrange.

Observatie!

Daca functia f este convexa si de clasa C² pe D, atunci conditiile cuprinse in teorema 11.6.13 sunt si suficiente pentru ca punctual critic conditionat (x₀,y₀ ) sa fie punct de extreme conditionat.Dupa cum se observa cu usurinta, in acest caz, forma patratica d²L(x₀,y₀) fiind pozitiv definita, punctul (x₀,y₀ )va fi punct de minim conditionat pentru f.

Ex5.

Sa se determine extremele functiei f(x,y)=xy cu legatura x²+y²=a².

Fie functia L(x,y)=xy+(x²+y²-a²)

Sa se determine punctele stationare.Observam ca

x²+y²-a²

Sa rezolvam sistemul

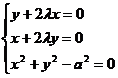
Sistemul

Nu trebuie sa aiba numai solutia nula si deci

=0,

De unde si

Daca rezulta ca x=-y si atunci, din x²+y²=a² obtinem x₁=, y₁=-, x₂=-, y₂=

Daca rezulta ca x=y si atunci, din ecuatia x²+y²=a² obtinem x₃==y₃ ,

x₄=-=y₄ .

Avem patru puncte stationare.

Pentru avem L₁(x,y)=xy+(x²+y²-a²).

Dar , de unde

Prin urmare, d²L₁(x_i,y_i)=dx²+dy²+2dxdy=(dx+dy)², i=1,2, ceea ce antreneaza ca punctele stationare (x₁,y₁) si (x₂,y₂) sunt puncte de minim.

Pentru , obtinem L₂(x,y)=xy-(x²+y²-a²).

Cum y-x , x-y, rezulta =-1, =-1,

In acest caz, d²L₂(x_i,y_i)=-dx²-dy²+2dxdy=-(dx-dy)², i=3,4, adica aceasta forma patratica este negative definite si, in consecinta, punctele stationare (x₃,y₃) si (x₄,y₄) sunt puncte de maxim.

Daca f este o functie convexa de o variabila, atunci (Lf) indica transformata Legendre a lui f.(Lf) se va dovedi ca este tot o functie convexa.Este definite de:

(Lf)(p)=(xp-f(x))

Geometric, (Lf)(p) este distanta maxima pe verticala dintre o linie a pantei p prin origine si f.

Fig1.

Functia convexa y=f(x), o parabola in acest caz, este desenata albastru.Linia y=px este desenata verde.Distanta pe verticala xp-f(x) este desenata rosu.distanta este maxima de la punctual x_p , unde tangenta la f(x)are panta p.

Daca f este diferentiabila, atunci clar maximul este atins la valoarea lui x_p , ce rezolva p=f'(x_p).

Solutia x_p  este unica datorita monotoniei lui f'.Atunci, transformata Legendre este:

(Lf)(p)= x_p p-f(x_p)

Observatie!

1.     Daca f este o functie concava atunci transformata legendre este -(L(-f)).

2.     Doua functii care sunt transformate Legendre a inselor sunt parabola si logaritmul.

Ex1.

Aratati ca, daca f(x)= atunci (Lf)(p)=.In particular, pentru m=1/2, o parabola este transformata Legendre a ei insasi.

Ex2.

Aratati ca, transformata Legendre a functiei f(x)=alog(x) este (Lf)(p)=alog(), unde loge=1.

In particular, pentru a=e, functia logarithm este insusi transformata Legendre.

Este remarcabil ca transformata Legendre a unei functii usoare, are nevoie sa nufie usoara.De fapt, pentru f(x)=a|x|ⁿ , (Lf)(p)=a(n-1)||^n/n-1 . In particular, daca n este un numar intreg, sa zicem 4, f este usoara de rezolvat, dar Lf are o putere fractionala 4/3.

Fig2.

Ex3.

Aratati ca transformata Legendre a functiei f(x)=ae^x/b este (Lf)(p)=(bp)log() , unde loge=1

Propozitia1

Transformata Legendre duce functii convexe in functii convexe.

Propozitia2

tdhj

Aici este o dovata geometrica a primei exprimari (P1):

Conform definitiei, pentru x, (Lf)(p)≥xp-f(x). descrieo linie dreapta in p si inegalitatea spun ca transformata Legendre in jumatatea planului deasupra acestei linii, si pentru un x special de pe linie.din moment ce aceasta este adevarata pentru toti x-icsi, aceasta arata ca transformata Legendre la intersectia la ½ planului. Deci este convexa.

Transformata Legendre este.aceasta inseamna ca L(Lf)=f,.Pentru a vedea asta luati g=(Lf).atunci de la definitie g(p)=p x_p -f( x_p ), p=f '(x_p ) , in timp ce (Lg)(x)=xp_x-g(p_x ), x=g'(p_x).

Vrem sa aratam ca f=(Lg).

Propozitia3

Daca p si x sunt legati de p=f'(x), atunci este de asemenea adevarat ca x=(Lf)'(p).In primul caz, p este dat ca o functie expicita a lui x si in celalalt. X este dat ca o functie explicita de p.

Intradevar, daca x_p rezolva p=f'(x_p ) atunci p_x care rezolva x=g'(p), trebuie sa coincide cu functia inverse a lui x_p.Aceasta este vazut de la inserarea definitiei transformatei Lagrange.

x=g'(p_x)=(p x_p-f(x_p))'= x_p+(p-f'(x_p)) x'_p = x_p

Acum inlocuieste definitia lui g in ecuatia pentru Lg:

(Lg)(x)=xp_x-g(p_x)=xf'(x)-(xp_x-f(x))=x(f'(x)-px)+f(x)=f(x).

Transformata legendre de mai multe variabile

Notiunea de transformata Legendre se extinde la cazul de mai multe variabile unde xRⁿ.

Ex.

Luati f a fi un paraboloid, adica f(x)= xAx

Notatia din dreapta este ca x este un vector si A este o matrice.Cand p este un vector p=f=ax si transformata legendre este de asemenea un paraboloid

(Lf)(p)=px_p-f(x_p)=pA^-1p-pa^-1p= pA^-1p

Ex

Gasiti transformata Legendre a ax-b

Transformata Legendre este un punct.Pentru p=a ia valoarea b, in timp ce pentru toti ceilalti p ia valoarea

Transformata Legendre partiala

Presupunem ca f(x,y)este convexa si o transformata Legendre cu privire la x singur:

g(p,y)=(px-f(x,y))

cu siguranta, g(p,y) este convexa in p.Dar despre y? In caz ca f(x,y)=f₁(x)+f₂(y) este clar atunci g(p,y)este concava in y.Este intotdeauna adevarat?Din fericire raspunsul este da.

Luati x=x(p,y) a fi solutie a lui p=f(x,y)

Atunci

g(p,y)=px-f(x,y)

Sa aratam ca g(p,y)este concave in y.

Luati 2u=x+z, 2v=x-z atunci

g(p,y₁)+g(p,y₂)=(xp-f(x,y₁)+zp-f(z,y₂))=(2up-f(u+v,y₁)-f(u-v,y₂))≤2(up-f(u,))=2g(p,

Transformata Legendre a functiei cu segmente liniare

Am vazut ca transformata Legendre a unei functii linire este o constanta.Aceasta inseamna ca daca o functie convexa are puncte liniare in regiunea punctelor liniare va trasa la un singur punct(sau ocazional, o parte orizontala).