
|
|
|
ETAPA LOCALA A OLIMPIADEI DE MATEMATICA
Clasa a VI-a
Enunt Problema nr.1
Se considera un unghi alungit ![]() si, in acelasi semiplan determinat de dreapta AB se
considera (n-1) semidrepte distincte care impart
si, in acelasi semiplan determinat de dreapta AB se
considera (n-1) semidrepte distincte care impart ![]() in n unghiuri, nIN, n 2. Aceste n
unghiuri formate au masurile (in grade sexagesimale) exprimate prin numere
naturale diferite.
in n unghiuri, nIN, n 2. Aceste n
unghiuri formate au masurile (in grade sexagesimale) exprimate prin numere
naturale diferite.
a) Sa se gaseasca valoarea maxima a numarului natural n;
b) Pentru valoarea lui n gasita la punctul a), dati un exemplu in care sa precizati masurile celor n unghiuri care se formeaza;
c) Sa se determine numarul maxim de unghiuri care se pot forma (in conditiile precizate in enunt) daca unul dintre unghiuri este drept.
Barem de corectare problema nr. 1
a) Pentru ca n (numarul de
unghiuri) sa fie maxim, trebuia ca masurile acestor unghiuri sa
fie cat mai mici. Deoarece masurile acestor unghiuri sunt exprimate prin numere
naturale diferite, cele mai mici valori pot fi: 10, 20,
, n0. Dar suma masurilor celor n unghiuri este 1800.
Inseamna ca 10+20+
+n0
1800 T
![]() T
T
![]() si cum n este
numar natural, n
18. Valoarea maxima a lui n este 18.
si cum n este
numar natural, n
18. Valoarea maxima a lui n este 18.
b) Un exemplu ar putea fi 10, 20, 30, , 160, 170, 270.
c) Daca unul dintre unghiuri este drept, revenim in cazul a) dar cu n-1 unghiuri a caror suma a masurilor este de 900.
10+20+
+(n-1)0
900 T
![]() T
T
![]() T
n
13. Valoarea maxima a lui n in acest caz este 13.
T
n
13. Valoarea maxima a lui n in acest caz este 13.
Enunt Problema nr.2
Demonstrati ca 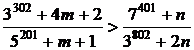 , pentru orice numere naturale m si n.
, pentru orice numere naturale m si n.
Barem de corectare problema nr. 2
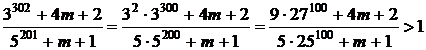
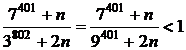
Din cele doua relatii rezulta imediat inegalitatea din enunt.
Enunt Problema nr.3
a) Exista numere de cinci cifre, cu cifrele distincte doua cate doua, formate cu cifrele 0, 1, 4, 6, 9 care, prin impartire la 3, dau restul 1?
b) Cate numere de cinci cifre, cu cifrele distincte doua cate doua, formate cu cifrele 0, 1, 4, 6, 9, sunt patrate perfecte?
Barem de corectare problema nr. 3
Se demonstreaza mai intai ca restul impartirii la 3 (si respectiv la 9) a unui numar natural si respectiv a sumei cifrelor sale este acelasi (pentru usurinta, se poate demonstra pentru numere de 5 cifre).
Cum ![]() si
si ![]() , avem
, avem ![]() . Deci restul impartirii numarului
. Deci restul impartirii numarului ![]() la 3 si respectiv
la 9 este egal cu restul impartirii numarului
la 3 si respectiv
la 9 este egal cu restul impartirii numarului ![]() la 3 si respectiv
la 9.
la 3 si respectiv
la 9.
a) Numerele de cinci cifre distincte care se pot forma cu 0, 1, 4, 6, 9 au suma cifrelor 20=M3+2. Inseamna ca restul impartirii oricarui numar cu forma indicata la 3 va fi egal cu 2. Nu exista numere de cinci cifre distincte formate cu 0, 1, 4, 6, 9 care sa aiba restul impartirii la 3 egal cu 1.
b) Orice numar natural are una din formele: 3k, 3k+1, 3k+2. Avem:
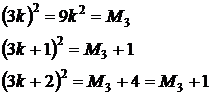
Inseamna ca, orice patrat perfect are forma M3 sau M3+1. Cum numerele naturale care respecta enuntul problemei sunt de forma M3+2, va rezulta ca nu exista patrate perfecte formate din cinci cifre distincte, cu cifrele 0, 1, 4, 6, 9.
Enunt Problema nr.4
Pretul unui obiect a fost majorat cu p% si apoi, noul
pret a fost micsorat cu q% din el astfel incat obiectul costa in
final cat a costat initial. Sa se arate ca ![]() IN.
IN.
Barem de corectare problema nr. 4
Fie x lei pretul initial al obiectului.
Dupa majorarea cu p%, obiectul cota acum ![]()
Dupa reducerea cu q%
din noul pret,
obiectul costa ![]()
Pentru ca pretul final va fi acelasi cu cel initial, vom avea:
![]() T (100 - q)(100 + p)=10000 T 10000+100p-100q-pq=10000 T 100(p-q)=pq T
T (100 - q)(100 + p)=10000 T 10000+100p-100q-pq=10000 T 100(p-q)=pq T ![]() =100IN.
=100IN.
Problema 5
Sa se arate ca daca un numar este divizibil cu 197 , atunci dublul numarului rezultat din ultimele doua cifre ale sale , adunat cu de 3 ori numarul ramas prin eliminarea acestor doua ultime cifre , formeaza de asemenea un numar divizibil cu 197.
Barem Problema 5
Problema 6
Sa se determine numerele rationale a, b, c, numerele naturale
pare k si numerele naturale n care satisfac conditiile a+b+c=12 si ![]()
Barem Problema 6
Din oficiu..1p
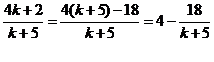 , k
, k
Problema 7
Fie numerele nenule a, b, c, d.Stiind ca ![]() , sa se calculeze
, sa se calculeze![]() .
.
Barem Problema 7
Problema 8
Se dau semidreptele [OA, [OB, [OC, [OD astfel incat
[OB si [OC sunt interioare unghiurilor
a)
Aratati ca ![]()
![]() .
.
b)
Daca
![]() , aratati ca
, aratati ca ![]() .
.
c)
Daca [ON este si bisectoarea
unghiului MOP, dovediti ca ![]() .
.
Barem Problema 8
![]() Din
oficiu1p
Din
oficiu1p
![]() a) Ajunge la
a) Ajunge la ![]() .1p
.1p
![]() Ajunge la
Ajunge la ![]() 1p
1p
![]() b)
Ajunge la
b)
Ajunge la ![]() 1,5p
1,5p
![]() c)
c) ![]() bisectoarea
bisectoarea ![]() ..1p
..1p
![]() bisectoarea
bisectoarea 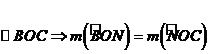 ..1p
..1p
![]() .2p
.2p
![]() Ajunge la
Ajunge la ![]() si
si ![]() .1p
.1p
![]() .0,5p
.0,5p
Problema nr. 9
Determinati numerele nenule a, b, c, invers proportionale cu numerele 5, 6 , 10 stiind
ca ![]() .
.
Barem pb 9
2p. Avem sirul de rapoarte egale: 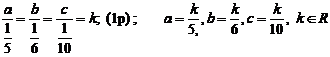 , k ≠
0, (1p)
, k ≠
0, (1p)
2p. Avand 9(a2 + b2 +
c2) = 7abc, (1p) ; obtinem 9![]() , (1p)
, (1p)
2p. 9k2![]() (1p 9k2
(1p 9k2![]() ;
; ![]() , k = 30 , (1p)
, k = 30 , (1p)
1p. Deci ![]() a = 6 , b = 5 , c = 3
a = 6 , b = 5 , c = 3
Problema nr. 10
Aratati ca patru numere naturale consecutive nu pot fi termenii unei proportii.
Cat ar trebui adunat (sau scazut) la al patrulea numar din sirul anterior, pastrand ordinea, pentru ca
impreuna cu celelalte trei sa formeze o proportie cu termeni naturali ?
Barem pb 10
a) 1p. Notam cele patru numere naturale cu : a , a + 1 , a + 2 , a + 3 , aIN
Daca s-ar forma o proportie, primul si ultimul ar fi termeni de acelasi fel : extremi sau mezi
1p. Presupunem ca avem
proportia de forma :![]() si a( a + 3 ) = (a +1)(a + 2),
si a( a + 3 ) = (a +1)(a + 2),
1p. a( a + 3 )= a2 + 3a ; (a +1)(a + 2) = (a+1)t=at +t =a(a+2)+ (a+2)= a2 + 2a + a +2 = a2 + 3a + 2, deci
a2 +3a = a2 + 3a + 2. Ultima relatie nu poate fi adevarata . Patru numere consecutive nu pot forma o proportie.
b) 1p. Deoarece a2 + 3a < a2 + 3a + 2 rezulta ca trebuie sa adunam la (a+3) un numar x pentru a obtine egalitate :
1p. a(a + 3+ x) = a2 + 3a + 2, a2 + 3a + ax = a2 + 3a + 2 , ax = 2 ,
![]() este numarul pentru a se
obtine proportie, ultimul termen fiind a + 3 +
este numarul pentru a se
obtine proportie, ultimul termen fiind a + 3 + ![]()
1p. Pentru a avea termeni naturali trebuie ca a sa fie divizor al lui 2 , deci a = 1 sau a = 2
1p. adica se obtine o proportie cu termini naturali pentru a = 1 si x = 2 sau a = 2 si x = 1
Problema nr.11
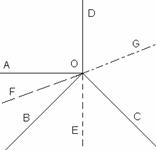
Fie <AOB , <BOC, <COD, <DOA, unghiuri formate in jurul punctului O. Bisectoarea lui <BOC si [OD
sunt semidrepte opuse. Daca [OD este perpendiculara pe [OA si mas(<AOB) = 450 , sa se arate ca:
a) OC este perpendiculara pe OB ;
b) Bisectoarele unghiurilor <AOB si <DOC sunt semidrepte opuse.
 Barem pb. nr 11
Barem pb. nr 11
a) 1p. Figura
1p. Construim [OE bisectoarea lui <BOC.
1p. Atunci mas(<EOB) = 1800 - [mas (<AOB) + mas (<AOD)] =1800 - ( 900 + 45 0) = 450 ,
1p. deci mas(<EOC) = 450 . Rezulta ca mas(<COB) = 900 si OC OD.
b) 1p. Avem mas(< COD) = 180 mas(< EOC) = 1800 450 = 1350
1p. Fie [OF bisectoarea <AOB si [OG bisectoarea <COD.
1p. Atunci mas(<FOG) = mas (< GOC) + mas (<COB) + mas (<BOF) =
= 670
in prelungire asa ca [OG si [OF sunt semidrepte opuse.
Problema nr 12
Unghiurile <AOB si <BOC sunt adiacente iar [OX si [OY sunt bisectoarele lor.
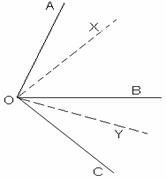 a) Daca OX OC si OY OA, calculati
masurile unghurilor considerate;
a) Daca OX OC si OY OA, calculati
masurile unghurilor considerate;
b) Daca semidreptele [OX si [OC , respective semidreptele [OY si [OA sunt in prelungire,
calculati masurile unghiurilor considerate.
Barem pb. 12
a) 1p. Figura
1p. 1) Fie mas(<AOX) = m , mas(<BOY) = n 1) notatii
2) mas(<AOB) = 2m 2) [OX bis. <AOB , ip
3) mas(<BOC) = 2n 3) [OY bis. <BOC , ip
1p. 4) mas(<AOB) + mas(<BOY) = mas (<AOY) 4) constr.,ip.
5) 2m + n = 900 5) 1,2
1p. 6) mas(<BOC) + mas(<BOX) = mas (<COX) 6) constr.,ip.
7) 2n + m = 900 7) 1,3
1p. 8) m = n , m = 300 , mas(<AOB) = 600 , mas(<BOC) = 600 8)5, 7, 4, 2
b) 1p. 9) mas(<AOY) = mas(<COX)= 1800 9) ip.
1p. 10) m = n = 600 , mas(<AOB) = mas(<BOC) = 1200 10) 5,7,9,
Problema nr.13
Adaugati trei cifre la dreapta numarului 523 astfel incat numarul obtinut sa se divida cu 7,cu 8 si cu 9.
Barem Problema nr.13
Fie N=![]() . Cum 7|N ; 8|N ; 9|N , rezulta ca 504|N (1)
. Cum 7|N ; 8|N ; 9|N , rezulta ca 504|N (1)
1 punct
Insa N=![]() = 523000+
= 523000+![]() = 1034
= 1034![]() 504 + 352 +
504 + 352 + ![]() (2)
(2)
1 punct
Din (1) si (2) 352+
![]() =504
=504![]() k (3)
k (3)
1 punct
Pentru k=1 ![]() =504-352
=504-352 ![]() =152
=152
1 punct
Pentru k=2 ![]() =1008-352
=1008-352 ![]() =656
=656
1 punct
Pentru
![]() egalitatea (3) nu mai
poate avea loc deoarece ar rezulta ca
egalitatea (3) nu mai
poate avea loc deoarece ar rezulta ca ![]() are mai mult de trei
cifre.
are mai mult de trei
cifre.
1 punct
Solutie
![]()
Problema nr. 14
II) Fie A=![]() si B=
si B=![]()
unde ![]() sunt cifre ale
sistemului zecimal iar n este un numar natural nenul.
sunt cifre ale
sistemului zecimal iar n este un numar natural nenul.
Sa se demonstreze ca daca 17|B atunci 17|A
Barem Problema nr. 14
![]()
![]() Notam X=
Notam X=![]() ; Atunci A=X
; Atunci A=X![]() 10 + an +8an A= X
10 + an +8an A= X![]() 10 + 9an .
10 + 9an .
1 punct 1 punct
B=X+6an
.
![]()
17|B 17| (X+6an)
X+6an=17![]() K ;
K ; ![]() X=17
X=17![]() K - 6
K - 6![]() an . (1)
an . (1)

![]() Din A= X
Din A= X![]() 10 + 9an si X=17
10 + 9an si X=17![]() K - 6
K - 6![]() an A= 10(17
an A= 10(17![]() K 6an ) + 9an A=170
K 6an ) + 9an A=170![]() K - 51
K - 51![]() an A=17(10
an A=17(10![]() K - 3
K - 3![]() an ) 17|A
an ) 17|A
1 punct
Problema nr.15
Demonstrati inegalitatea : ![]()
Barem Problema nr.15

![]()
![]()
![]()
![]()
Problema nr.16
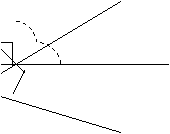
Se considera unghiul ascutit XOY . In semiplanul determinat de (OX si in care nu se afla Y se duc perpendicularele (OA si OB pe (OX, respectiv pe (OY . Se noteaza cu (OC bisectoarea unghiului BOX.
a) Daca m(![]() XOC) este cu 20o mai mare decat m(
XOC) este cu 20o mai mare decat m(![]() XOY), sa se afle m(
XOY), sa se afle m(![]() XOY).
XOY).
b) Daca (OX
este bisectoarea ![]() YOC , atunci m(
YOC , atunci m(![]() COY)= m(
COY)= m(![]() XOB)
XOB)
Barem Problema nr.16
A B
C
O X
Y
1 punct 1 punct
![]()
![]() a) Fie m(
a) Fie m(![]() =ao si m(
=ao si m(![]() =2bo .
=2bo .
b=a+20o (1)
(OC este bisectoare m(![]() = m(
= m(![]() = bo
= bo
1 punct
![]() Din
ipoteza (OB
Din
ipoteza (OB ![]() (OY
(OY ![]() m(
m(![]() =90o
=90o
2b+a=90o (2)
m(![]() =2b+a
=2b+a
1 punct
Din (1) si (2) 2a+40o + a = 90o 3a=50o a= 16o 40
1 punct
b) (OX
bisectoarea ![]() m(
m(![]() = m(
= m(![]()
![]() a=b (3)
a=b (3)
0,5 puncte
(OC bisectoarea ![]() m(
m(![]() )=2b
)=2b
0,5 puncte
m(![]() ) + m(
) + m(![]() )=90o 2b+a=90o
(4)
)=90o 2b+a=90o
(4)
Din (3) si (4) a=300
1 punct
![]() m(
m(![]() )=2b ; b=a=30o m(
)=2b ; b=a=30o m(![]() )=60o
)=60o
![]()
![]()
m(![]() )=60o
)=60o
MODEL DE SUBIECT NR. 1
1. Determinati numerele naturale a, b, c astfel incat sa aiba loc relatia:
![]() .
.
2. Trei vanzatori au caiete cu acelasi pret. Primul a marit pretul cu 20% si apoi l-a
micsorat cu acelasi procent, al doilea a micsorat mai intai pretul cu 20% si abia
apoi l-a marit cu acelasi procent iar al treilea a lasat pretul neschimbat.
De la care vanzator ai cumpara acum si de ce?
3. Fie triunghiul isoscel
ABC cu (AB) s (AC) si punctele D, E IBC, astfel incat BI(DC), CI(BE) si (BD) s(CE). Perpendiculara in D pe AD intersecteaza perpendiculara in E pe
AE in punctul F. Sa se arate ca (AF este bisectoarea unghiului ![]()
4. Demonstrati ca un numar cu n cifre identice, n>1, nu poate fi patrat perfect.
BAREM MODEL DE SUBIECT NR. 1
Sub.
Pct
1.
0.5
egaleaza rapoartele cu k
1
c+3=5/k = n natural , de unde k=5/n
1
a+1 = 4 5/n si b+2 = 3 5/n si sunt numere naturale
2
cum 3 si 4 sunt prime intre ele rezulta ca n este divizor al lui 5
2
n= 5 , k = 1 solutia (3, 1, 2)
0.5
n=1, k= 5, c nu este natural
2.
3
primul vanzator scade pretul cu 4 %
3
al doilea vanzator scade pretul cu 4 %
1
putem cumpara de la oricare dintre primii doi pentru ca au acelasi pret final mai mic decat cel initial
3.
1
figura completa
2
demonstreaza ca DABDsDACE si obtine
AD=AE si ![]() DABs
DABs![]() EAC ,
EAC ,![]() ADBs
ADBs![]() AEC
AEC
3
demonstreaza ∆ADFs∆AEF
(LLL)si obtine ![]() DAF s
DAF s![]() EAF
EAF
obs - daca elevii folosesc teoreme de congruenta pentru triunghiuri dreptunghice vor primi punctaj maxim
1
prin diferenta de unghiuri congruente, ![]() BAFs
BAFs![]() CAF, deci (AF bisectoarea
CAF, deci (AF bisectoarea ![]() BAC
BAC
4.
1
ultima cifra a unui patrat perfect nu poate fi 2, 3 7 sau 8
1
patratele perfecte sunt de forma 4k sau 4k+1
3
verifica si deduce ca singura posibilitate ramasa este 4444
2
44444 nu poate fi patrat perfect deoarece este produsul dintre un patrat perfect 4 si un numar care nu este patrat perfect 11111



SET DE PROBLEME PROPUSE
PROBLEME CU RASPUNS DIRECT
1. Daca 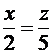 , cat la suta reprezinta z din x? Raspuns
.
, cat la suta reprezinta z din x? Raspuns
.
2. Cate fractii de forma 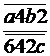 se simplifica
prin 36? Raspuns
.
se simplifica
prin 36? Raspuns
.
3. Cifra a din relatia: 0,(a) + 0,0(a) + 0,00(a) = 0,37 este .
4. Valoarea expresiei E = 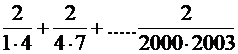 este
..
este
..
5. Un numar natural impartit la 7 si respectiv 8 da resturile 6 si respectiv 5. Restul impartirii acestui numar la 56 este
6. Raportul dintre masura suplementului si
masura complementului unui unghi este ![]() . Masura
unghiului este
..
. Masura
unghiului este
..
7. Fie unghiurile adiacente AOB si BOC. Daca m![]() = 700 si masura unghiului format de
bisectoarele celor doua unghiuri este de 510 atunci m(AOB) este
.
= 700 si masura unghiului format de
bisectoarele celor doua unghiuri este de 510 atunci m(AOB) este
.
8. Se considera 5 puncte distincte astfel incat oricare trei dintre ele sunt necoliniare. Numarul de triunghiuri determinate de cate trei din aceste puncte este
9. Se da numarul 1 2 3 2003 2. Restul impartirii acestui numar la 50102 este ..
5 7m = 7n 2
11. Fie numerele naturale x si y astfel incat
x 16 = 15 (16 + 162 + 163 + . + 16n-1), n 2, n I N,
y 13 = 2p (5 + 52 + 53 + . + 5p), p 1, p I N.
Stabiliti care din aceste numere este patrat perfect.
12. Unghiurile AOB, BOC, COD, DOE sunt adiacente si cu interioarele disjuncte astfel incat punctele A, O si E sunt coliniare. Masurile unghiurilor AOB, BOC, COD, DOE formeaza respectiv cu patru numere naturale nenule consecutive, rapoarte egale. Sa se demonstreze ca doua dintre unghiuri sunt complementare.
13. Doi elevi, lucrand separat, au rezolvat impreuna 520 de probleme, desi isi propusesera sa rezolve 425. Stiind ca primul a rezolvat cu 25%, iar al doilea cu 20% mai mult decat si-au propus, aflati cate probleme a rezolvat fiecare.
14. Determinati cele mai mici numere naturale consecutive a, b, c, d (0<a<b<c<d) stiind ca sunt divizibile respectiv cu numerele 8, 7, 6, 5.
15. Determinati numerele naturale a, b, c stiind ca sunt direct proportionale respectiv cu numerele 2, a, b si a+4b+4c=2028.
16. In triunghiul isoscel ABC se duc inaltimea AD si bisectoarea AA (D,A BC). Aflati masurile unghiurilor triunghiului ABC stiind ca DB=DA.
17. Fie x si y numere naturale. Aratati ca:
a) Daca 3x+5y![]() 13 atunci 33x+55y
13 atunci 33x+55y![]() 13 .
13 .
b) Daca 3x+5y![]() 13 atunci 16x+18y
13 atunci 16x+18y![]() 13 .
13 .
c) 3x+5y![]() 13 daca si
numai daca 7x+3y
13 daca si
numai daca 7x+3y![]() 13 .
13 .
18. a) Fie a , b![]() N numere prime consecutive diferite de 2 . Daca a+b=2n ,
aratati ca n este numar compus .
N numere prime consecutive diferite de 2 . Daca a+b=2n ,
aratati ca n este numar compus .
b) Calculati suma cifrelor
numarului A=8∙![]() -5264 .
-5264 .
19. Numerele naturale de la 1 la 2004 sunt aranjate ca mai jos . In ce rand este numarul 2004 . ( Justificati raspunsul )
Randul 1: 3 11 19
Randul 2 : 2 6 10 14 18 22 ![]()
Randul 3 :1 5 9 13 17 21 25
Randul 4 : 4 8 12 16 20 24 ![]()
Randul 5 : 7 15 23
Prof. Constantin Berbecel
20. Se considera punctele coliniare A , O , B in aceasta ordine. De aceeasi parte a dreptei AB consideram punctele C si D astfel incat OC ![]() OD si semidreapta [OC este inclusa
in interiorul unghiului AOD. Fie [OE , [OF , [OG , [OH respectiv bisectoarele unghiurilor AOC , COD , BOD
si COB .
OD si semidreapta [OC este inclusa
in interiorul unghiului AOD. Fie [OE , [OF , [OG , [OH respectiv bisectoarele unghiurilor AOC , COD , BOD
si COB .
a) Aratati ca OE![]() OH .
OH .
b) Stiind ca masurile unghiurilor EOF si FOG sunt direct proportionale cu numerele 4 si 5 , sa se afle masurile unghiurilor AOC si BOD .
21. a)Stabiliti daca numerele a=1.2.3. .n+1; b=1.2.3. .(n+1)+1, unde nIN*, sunt prime intre ele.
b)Sa se determine nIN astfel ca
fractia ![]() sa fie reductibila. Pentru cate valori ale lui n,
fractia este reductibila?
sa fie reductibila. Pentru cate valori ale lui n,
fractia este reductibila?
22. Determinati numarul de elemente din multimea:
S=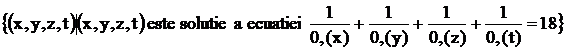 iar x, y, z, t sunt cifre in baza 10.
iar x, y, z, t sunt cifre in baza 10.
23. Fie m produsul primelor 2003 numere naturale impare
si n produsul primelor 2003 numere naturale prime. Aflati ultimele
doua cifre ale numarului 7![]() .
.
24. Fie AOB, BOC, COD, DOE si EOA unghiuri in jurul unui
punct si [OX si [OY bisectoarele unghiurilor AOB si BOC.
Stiind ca masura unghiului XOY este de 800, m(COD)=![]() m(DOE) si m(DOE)=
m(DOE) si m(DOE)=![]() m(AOE), aflati masurile unghiurilor AOC, COD, DOE
si EOA. Daca raportul masurilor unghiurilor AOB si BOC este
m(AOE), aflati masurile unghiurilor AOC, COD, DOE
si EOA. Daca raportul masurilor unghiurilor AOB si BOC este
![]() , aflati masurile lor.
, aflati masurile lor.
25. Se considera unghiul obtuz AOB si dreptele a ,b concurente in O , astfel incat a OA si
b OB . Fie C si D doua puncte arbitrare CIa , DIb
a) Aratati ca daca C si D sunt ambele in interiorul unghiului AOB sau in exteriorul aceluiasi
unghi , atunci unghiurile AOB si COD sunt suplementare .
b) Fie C si D in interiorul unghiului AOB CIa , DIb . Se stie ca masurile unghiurilor AOB
si COD indeplinesc conditia
![]() .
.
Sa se demonstreze ca daca [ OM si [ON sunt bisectoarele unghiurilor AOD si BOC ,
atunci [ OD si [OC sunt bisectoarele unghiurilor MOC si DON .
26. Fie triunghiul isoscel
ABC ( AB=AC ) si punctele ![]()
![]()
a)
Aratati ca ![]() .
.
b) Daca 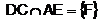 aratati
ca
aratati
ca ![]() .
.
27. Mai multe patrate identice pot fi asezate pe 25 de randuri , fiecare rand avand cu doua patrate mai mult decat cel anterior ( ca in desenul de mai jos).
![]()
a) Cate patrate sunt pe ultimul rand ?
b) Cate patrate , identice cu cel de pe primul rand , sunt in total ?
c) Cate dreptunghiuri diferite (doua dreptunghiuri sunt diferite daca au dimensiuni diferite ) se pot construi utilizand toate patratele ( justificati raspunsul) ?
28. Se considera fractiile
de forma : ![]() .
.
a) Aratati ca daca fractiile nu sunt ireductibile , atunci ele se simplifica cu 19 .
b) Sa se determine cele mai mici trei numere naturale n pentru care se obtin fractii reductibile .
29.Fie 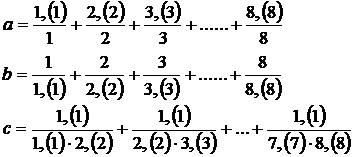
Aratati ca :
a) ![]() si
si ![]() are 7 divizori;
are 7 divizori;
b) ![]() si este prim;
si este prim;
c) ![]()
30.Sa se determine bumerele prime x,y,z astfel incat 2x+5y=99 si 3y+4z=101
31.Se dau numerele :
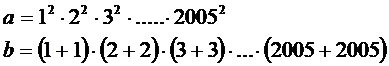 Comparati
Comparati ![]() cu
cu ![]()
32.Fie unghiurile ![]() si
si ![]() adiacente , cu
masurile de a si respectiv b,
adiacente , cu
masurile de a si respectiv b, ![]() . Numerele a si b verifica relatiile :
. Numerele a si b verifica relatiile :
![]()
In interiorul unghiului ![]() se construiesc
semidreptele
se construiesc
semidreptele ![]() si
si ![]() astfel incat
astfel incat ![]() . Semidreptele
. Semidreptele ![]() si
si ![]() sunt respectiv perpendiculare pe
sunt respectiv perpendiculare pe ![]() si
si ![]() , fiind situate in acelasi semiplan
determinat de dreapta OC.
, fiind situate in acelasi semiplan
determinat de dreapta OC.
a) Determinati a si b.
b)
Calculati ![]()
33.Sa se arate ca daca un numar este divizibil cu 197 , atunci dublul numarului rezultat din ultimele doua cifre ale sale , adunat cu de 3 ori numarul ramas prin eliminarea acestor doua ultime cifre , formeaza de asemenea un numar divizibil cu 197.
34. Sa se
determine numerele rationale a, b, c, numerele naturale pare k si numerele
naturale n care satisfac conditiile a+b+c=12 si ![]()
35.Fie numerele nenule a, b, c, d.Stiind ca ![]() , sa se calculeze
, sa se calculeze![]() .
.
36.Se dau semidreptele [OA, [OB, [OC, [OD astfel incat [OB si [OC sunt
interioare unghiurilor
d)
Aratati ca ![]()
![]() .
.
e)
Daca
![]() , aratati ca
, aratati ca ![]() .
.
f)
Daca [ON este si bisectoarea
unghiului MOP, dovediti ca ![]() .
.
Problema nr.37
Se considera 10 numere naturale nenule dinstincte cu suma 275,cu proprietatea ca daca produsul a doua numere dintre acestea este multiplu de 5 atunci si suma celor doua numere este multiplu de 5. Atunci :
a) Daca produsul a doua dintre cele 10 numere este multiplu de 5 atunci ambele sunt divizibile cu 5.
b) Sa se determine cele 10 numere stiind ca unul dintre ele este 5.
Problema nr.38
Se considera trei puncte A,B,C distincte situate pe aceeasi dreapta astfel incat B sa fie situat intre A si C.Fie M mijlocul lui [AB] si N mijlocul lui [BC]. Sa se arate ca:
(4p) a)AC=2·MN
(3p) b)Daca segmentele [MN] si [AC] au acelasi mijloc atunci AB=BC.
Problema nr.39
Se considera unghiurile AOB, BOC, COD, DOE, EOF si FOA in jurul punctului O. Unghiurile AOB si DOE sunt opuse la varf, iar m(COD)=m(AOF).
(3p) a) Sa se arate ca m(BOC)=m(EOF).
(4p) b) Daca (OM si(ON sunt bisectoarele unghiurilor AOB, respectiv COD, sa se arate ca m(MON)>90˚.
Problema nr.40
Punctele A, B, C, D sunt situate pe o dreapta d in ordinea data. Este adevarata egalitatea:
![]()
Problema nr.41
a) Sa se arate ca intre oricare doua puteri naturale consecutive ale lui 3 se afla cel putin o putere a lui 2.
b) Exista doua puteri naturale consecutive ale lui 3 intre care sa gasim trei puteri distincte ale lui 2?
Problema nr.42
Fie AB si CD doua drepte concurente, ![]() Fie
Fie ![]() bisectoarea unghiului
AOC,
bisectoarea unghiului
AOC, ![]() bisectoarea unghiului
POB si
bisectoarea unghiului
POB si ![]() bisectoarea unghiului
TOD.
bisectoarea unghiului
TOD.
a) Daca ![]() aflati
aflati ![]()
b) Daca ![]() aflati
aflati ![]()
Problema nr.43
Fiind dat numarul natural nenul n, demonstrati ca:
![]()
Problema nr.44 Fie unghiul ascutit AOB si semidreptele
[OC si [OD astfel incat m (![]() DOB) = 900 si m (
DOB) = 900 si m (![]() COA) = 900, iar interioarele unghiurilor AOC
si BOD sunt disjuncte.
COA) = 900, iar interioarele unghiurilor AOC
si BOD sunt disjuncte.
a) Aratati ca unghiurile AOB si COD sunt suplementare;
b) Daca [OE este bisectoarea unghiului AOB, iar OF este bisectoarea unghiului COD, aratati ca punctele E, O, F sunt coliniare.
c) Daca [OM este bisectoarea unghiului BOC, sa se arate ca masura unghiului FOM este constanta, indiferent de masura unghiului AOB.
Problema nr.45 Numerele x si y sunt direct proportionale cu 2 si 4, iar z este media aritmetica a numerelor x si y.
a)
Aflati valoarea raportului ![]() .
.
b) Aflati numerele x, y si z stiind ca suma lor este 36.
Problema nr.46 a) Sa se arate ca media aritmetica a unor numere naturale consecutive este un numar natural daca numarul numerelor naturale este impar .
b) Media aritmetica a unor numere consecutive este 4 . Aflati numerele .
Problema nr.47
a) Se considera numarul natural x = 4n , unde n IN . Se stie ca x are 90 de cifre .
Sa se demonstreze ca o cifra a lui x se repeta de cel putin 10 ori .
b) Sa se scrie numarul: 1002008 , sub forma de suma a patru cuburi perfecte de numere naturale.