
|
|
|
Atunci cand constituim un esantion de studiu, nu facem decat sa utilizam doar unul dintre esantioanele posibil a fi selectionate (alese, constituite, extrase) din populatia cercetarii. Daca am selecta mai multe esantioane din aceeasi populatie, fiecare dintre ele ar fi caracterizat prin indicatori sintetici specifici, vor avea, fiecare, media si abaterea lor standard. Imaginea de mai jos sugereaza situatia descrisa:

Daca fiecare dintre cele patru esantioane de valori are propria sa medie, atunci distributia mediilor tuturor esantioanelor extrase se numeste distributia mediei de esantionare sau, mai scurt, distributia de esantionare. La randul ei, distributia mediilor are si ea o medie, numita medie de esantionare, si care se calculeaza, evident, dupa urmatoarea formula:
![]()
unde μ este media populatiei, valorile m sunt mediile fiecarui esantion constituit, iar k este numarul esantioanelor.
Daca am extrage toate esantioanele posibile dintr-o populatie, atunci media de esantionare este identica cu media populatiei. Pentru exemplificare, sa presupunem ca avem o "populatie" constituita din valorile 1,2,3,4 si sa ne propunem constituirea tuturor esantioanelor posibile de cate 3 valori. Tabelul de mai jos ilustreaza aceasta situatie:
Populatia
Esantioane
Distributia mediei de esantionare
1
1,2,3
M1=2.00
2
1,2,4
M2=2.33
3
3,4,1
M3=2.67
4
2,3,4
M4=3.00
μ=2.5
σ=1.29
Toate esantioanele posibile pentru N=3
Σ=10.00
m=10/4=2.5
Asa cum se observa, daca extragem toate esantioanele posibile (in acest caz 4) dintr-o populatie de valori, atunci media mediilor esantioanelor extrase (denumita medie de esantionare) este identica cu media populatiei (in cazul dat: m=μ=2.5). Datele din tabel ne mai arata si faptul ca media fiecarui esantion variaza in jurul mediei de esantionare. De aceea ele pot fi considerate o estimare a acesteia din urma, in ciuda impreciziei pe care o contine fiecare. Aceasta imprecizie se numeste eroare de estimare. Desigur, exemplul are o valoare de ilustrare teoretica deoarece, in practica, niciodata nu se ajunge la selectarea tuturor esantioanelor posibile dintr-o anumita populatie de valori.
Distributiei de esantionare nu are aceeasi imprastiere ca si a distributiei valorilor variabilei de origine. Aceasta pentru ca, la nivelul fiecarui esantion o parte din imprastierea totala este "absorbita" de media fiecarui esantion in parte. Cu cat esantioanele sunt mai mari, cu atat media fiecarui esantion tinde sa fie mai apropiata de media variabilei originale si, implicit, abaterea standard a distributiei de esantionare este mai mica prin comparatie cu abaterea standard a variabilei.
Exemplu: Sa consideram populatia valorilor 1,2,3,4,5,6,7,8,9,10, pentru care am calculat m=5.5 si s=3,0276. Am extras, cu ajutorul unui program statistic, cinci esantioane aleatoare (pentru usurinta calculelor, am ales pentru fiecare esantion N=3). Iata cum se prezinta mediile si abaterile standard pentru cele cinci esantioane selectate:
m1=5.00
m2=4.5
m3=4.0
m4=2.5
m5=5.5
s1=5.65
s2=4.94
s3=4.24
s4=2.12
s5=6.36
In acest exemplu, cele cinci esantioane nu sunt toate ci doar o parte din esantioanele posibile de 3 valori extrase din populatia cercetata. Media distributiei de esantionare:
![]()
In
ceea ce priveste imprastierea distributiei de
esantionare, aceasta este, asa cum am spus, mai mica decat
imprastierea variabilei la nivelul intregii populatii, deoarece
o parte a imprastierii generale se concentreaza, si se
"pierde", in media fiecarui esantion extras. Ca urmare, abaterea standard
a distributiei de esantionare este o fractiune din abaterea
standard a populatiei, fiind dependenta de marimea
esantionului. Mai precis, fara a intra in detalii explicative, abaterea standard a distributiei de
esantionare este egala cu ![]() din abaterea standard a populatiei, unde
N este volumul esantionului.
din abaterea standard a populatiei, unde
N este volumul esantionului.
Deoarece imprastierea mediei de esantionare arata cat de mult se abat aceste medii de la media populatiei, abaterea standard a mediei de esantionare este denumita eroare standard a mediei si se calculeaza cu formula:
![]()
(formula 3.1)
unde sm este eroarea standard a mediei de esantionare, s este abaterea standard a populatiei iar N este volumul esantionului.
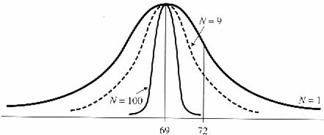
Figura alaturata sugereaza foarte bine modul in care, prin cresterea volumului esantionului, media esantionului se apropie tot mai mult de media populatiei, cu alte cuvinte, comporta o eroare din ce in ce in mai mica fata de aceasta.
Expresia de "eroare standard a mediei" poate fi mai greu de inteles, dat fiind faptul ca este folosita pentru a defini un indicator al imprastierii, in timp ce are in compunere cuvantul "medie". Trebuie insa sa retinem faptul ca acest indicator masoara cat de departe poate fi media unui esantion de media populatiei din care a fost extras. Altfel spus, cata "eroare" poate contine media unui esantion in estimarea mediei populatiei. Avand in vederea faptul ca la numitor avem o expresie bazata pe N (volumul esantionului), este limpede de ce, cu cat esantionul este mai mare cu atat eroarea standard a mediei este mai mica.