Derivata dupa un versor

Derivata dupa un versor

Pentru functii de mai mulkte variabile reale am putea considera un gen de derivata a functiei f dupa directii, adica limita raportului corespunzator de cresteri sa fie luata dupa "puncte care se gasesc pe anumite drepte ce trec prin acel punct".

Fie v=(v₁,v₂,..,v_n) - versor din Rⁿ , adica un vector vRⁿ cu ||v||=1.

Fie D o multime deschisa din Rⁿ .Daca aint D, vom numi dreapta prin a de directie v multimea:

(1)  

Definitia3

Fie f:DR, D=un deschis din Rⁿ

a) Spunem ca f admite derivata in a dupa versorul v, daca ().

Vom nota in acest caz valoarea limitei prin (a)

b)Daca (a) R vom spune ca f este derivabila in a dupa versorul v.

Observatie!

Intrucat a int D conform definitiei () S(a,) D.(a-punct de minim)

Atunci , daca consideram t(-,), toate punctele x=a+tv se vor gasi, de asemenea, in sfera S(a,), deoarece: ||(a+tv)-a||=||tv||=|t|||v||=|t|<.

Atasam functiei f functia : φ:(-,)R definite prin:

(t)=f(a+tv), t(-,).

Calculam derivate lui f dupa versorul v in punctual a:

(a)== ='(0)observam ca derivate lui f dupa versorul a este tocmai derivate obisnuita a functiei reale in origine.

Daca notam x=a+tv x-a este coliniar cu v.

Daca interpretam t ca abscisa punctului x pe dreapta ce trece prin a si are directia v (a)= (limita se realizeaza pe dreapta ce trece prin a si are directia v ).

Exemplu:

1)Sa se calculeze derivate dupa un versor oarecare u=(u₁,u₂)R² pentru f:R²R , f(x,y)=

Definitie4

I)spunem ca functia f:DR are derivate partiala in raport cu variabila x_k in punctual a daca ()(a), unde k iar se numeste derivate lui f in raport cu x_k in punctual a.

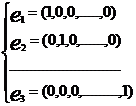baza canonica in Rⁿ

Notam (a ) sau f'x_k(a)

II) Spunem ca f:DR este derivabila partial in raport cu variabila x_k in punctual a daca (a)R.

III) Spunem ca f:DR este derivabila partial in raport cu x_k pe D daca f este derivabila partial in raport cu variabila x_k in orice punct aD.

Observam ca :

(1) (a)=(a)=

Pentru n=2 (1) obtinem

(2):

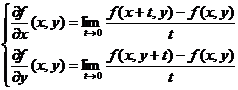
pentru n=3 obtinem

(3):

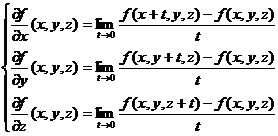
Exemplu

Fie f:DR, f(x,y)=xln(xy), (x,y)D=

Sa se calculeze derivatele partiale

(xln(xy))'_x=x'ln(xy)+x(ln(xy))'=ln(xy)+x=ln(xy)+=ln(xy)+1, (x,y)D

=(xln(xy))'_y=x'ln(xy)+x(ln(xy))'=x (x,y)D

Definitia5

Fie f:DR, unde D este un deschis din Rⁿ.

I) Spunem ca f este derivabila partial pe D daca F este derivabila partial in orice punct aD in raport cu toate variabilele x_k.In acest caz, se pot defini n functii :DR, k=1,2,.,n numite derivatele partiale ale lui f pe D.

II) Spunem ca f este de clasa C¹ pe D daca f este derivabila partial pe D iar functiile cu k=1,2,.,n sunt continue pe D

NotamfC¹(D).

Observatie!

1) Stim ca,daca f-diferentiabila intr-un punct, atunci f este in mod necesar continua in acel punct.

2)Se pune problema daca si functiile derivabile dupa un versor poseda proprietatea de continuitate.

Exemplu

Fie functia f:R²R definite prin:

f(x,y)=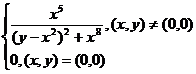

fie v=(cos,sin [0,2)-versor arbitrar

pentru t0 si a=(0,0) (t)=f(0+tv)=f(tcos,tsin

daca 0,2 =0

f-derivabila in (0,0) pentru versor v=(cos,sin) cu 0,

Daca =0 iar

Pentru v=

In concluzie f-derivabila in origine dupa orice versor v.

Continuitatea

Daca consideram sirulx_n=( ) de puncte situate pe parabola y=

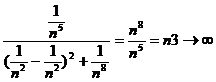
atunci x_n(0,0) f( functia f nu este continua in (0,0).

Sa cercetam care este raportul de generalitate intre notiunea de functie diferentiabila in punct si de functie derivabila dupa un versor v in acel punct.

Teorema8

Fie D un deschis din Rⁿ si f:DR.

Daca f este diferentiabila in punctul aD , atunci f este derivabila in a, dupa orice versor v si in plus are loc egalitatea:

(*)

Dem.

Fie v un versor din Rⁿ.

Cum aintD () S(a,r)D.

Pentru tS(a,r)

f-diferentiabila in a T:RⁿR, :D cu   a.i.

f(a+tv)=f(a)+T(a+tv-a)+||a+tv-a||(a+tv),t(-r,r)

f(a+tv)-f(a)=T(tv)+||tv||, t(-r,r)

De aici pentru t(-r,r)

Cum iar () f-derivabila dupa versorul v in punctual a iar

Observatie!

Reciproca acestei teoreme nu este adevarata. ()functii derivabile dupa orice versor, deci si derivabile partiale intr-un punct, care nu sunt diferentiabile in acel punct.

Consecinta

Teorema9(pune in evidenta o formula de calcul pentru diferentiala unei functii diferentiabile f:DR, DR_n, D=o multime deschisa)

FieDd un deschis din Rⁿ si fie f:D

Daca f este diferentiabila in punctual a, atunci f este derivabila partial in raport cu toate variabilele x_k si in plus:

iar df(a)=

=aplicatia de proiectie definite pe Rⁿ , prin x_k  , x=(x₁,x₂,...,x_n)Rⁿ .

Dem.

Daca f este diferentiabila in punctual aconform reoremei anterioare ca f este derivabila in a dupa orice versor v si in plus:

(1)

In particular, daca v=e_k (2), k=

Fie x-punct arbitrar din Rⁿ si fie e₁,e₂,..,e_n=baza canonica din Rⁿ.

Atunci x=(x₁,x₂,..,x_n) se poate acrie x= (combinatie liniara)

Cum df(a):RⁿR -operator liniar

df(a)(x)=(df(a))( )=

cum xRⁿ=arbitrar df(a)=

corolar

Teorema10(contine o formula de calcul pentru derivate dupa un versor intr-un punct, pentru o functie diferentiabila)

Fie D un deschis din Rⁿ si v=(v₁,v₂,.,v_n)-versor din Rⁿ. Daca f:D este diferentiabila in punctual aD, atunci derivata dupa versorul v in punctual a este data de formula:

(12)

Dem.

Daca f-diferentiabila in punctul aD f-derivabila in a, dupa versorul v si in plus are loc:

Teorema11 (criteriul de diferentiabilitate)

FieD o multime deschisa din Rⁿ si f:D

Daca f este derivabila partial(admite derivate partiale) pe o intreaga vecinatate a punctului aintD iar derivatele partiale sunt continue in a, atunci f este diferentiabila in a.

Dem.

Fie a=(a₁,a₂,...,a_n)D

Pp. fara a micsora generalitatea ca V=S(a,r)

Daca x S(a,r) f(x)-f(a)=f(x₁,x₂,..,x_n)-f(a₁,a₂,.,a_n)= [f(x₁,x₂,.,x_n)-f(a₁,x₂,..,x_n)]+[f(a₁,x₂,.,x_n)-f(a₁,a₂,..,a_n)]+..+[f(a₁,a₂,..,a_n-1,x_n)-f(a₁,a₂,.,a_n)]

f-derivabila partial in raport cu x₁ pe S(a,r)

fie g₁(t)=f(t,x₂,x₃,.,a_n) cf th Lagrange () (x₁,a₁) a.i. f(x₁,x₂,.,x_n)-f(a₁,x₂,..,x_n)=(x₁-a₁)(,x₂,..,x_n)

=f(a₁,t,x₃,.,x_n)cf th Lagrange () (x₂,a₂) a.i f(a₁,x₂,.,x_n)-f(a₁,a₂,x₃,.,x_n)=(x₂-a₂)(a₁,,x₃,.x_n).

Repetat procedeul (x₁,a₁),..,(x_n,a_n) a.i f(x)-f(a)=(x₁-a₁) (,x₂,..,x_n)+(x₂-a₂) (a₁,,x₃,.x_n)+.+(x_n-a_n)(a₁,a₂,., a_n-1,)

Cf th df(a)(x)= , xRⁿ

Daca f-diferentiabila in punctual a T=df(a) T(x-a)= ,xS(a,r) xS(a,r), xa.

= ..+,

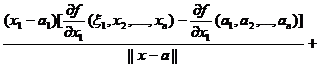
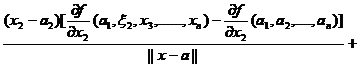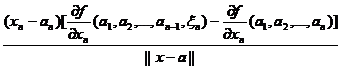Intrucat ≤1, k=

-derivatele partiale ale lui f sunt continue in a=() () limita membrilor (2) pentru xa=0 f-diferentiabila in punctul aD.

Corolar

Fie D o multime deschisa din Rⁿ .

Daca f:DR este de clasa C¹ pe D atunci f-diferentiabila pe D.

Definitia6:

Fie D un deschis din Rⁿ si fie F:DR^m , F=(f₁,f₂,..,f_m), in care f_i:D, i=

I)Spunem ca functia F este derivabila partial in aD(derivabila partial pe D), daca functie f_i , i= este derivabila partrial in a(respective partial pe D)in raport cu toate variabilele x₁,x₂,..x_n.

II)Spunem ca functia F este de clasa C¹ pe D , notat FC¹(D), daca toate functiile f₁,.,f_m sunt de clasa C¹ pe D.

Definitia+criteriul de diferentiabilitate

Propozitie

Daca F:DR^m ,unde D este un deschis din Rⁿ, este de clasa C¹ pe D, atubcu F este diferentiabila pe D.

Observatie!

Stim ca pr_k :RⁿR^m, operator liniar d(pr_k)(a)=pr_k sau dx_k(a)=pr_k

(11)df(a)=pr_k (11') df(a)= ·dx_k(a)

Daca f-diferentiabila in aD, avem:

(11'') df=dx_k

n=2 (11'')df=dx+dy

n=3 df= dx+dy+dz

exemplu

fie functia f:R³R definita prin f(x,y,z)=xy²+x²yz+y³

sa se scrie diferentiala acestei functii in punct curent

(x,y,z)=y²+2xyz

(x,y,z)=2xy+x²z+3y²

(x,y,z)=x²y

df(x,y,z)=( y²+2xyz)dx+(2xy+x²z+3y²⁾dy+ (x²y)dz

Sse scrie diferentiala in punctual (1,1,1) calculate in punctual h=(1,0,-1) df(1,1,1)(1,0,-1)=3·1+6·0+1·(-1)=3+0-1=2

Matrice jacobiana

Pp ca avem o functie F:DR^m,unde D este un deschis din Rⁿ, diferentiabila intr-un punct aD.Conform teoremei8 F este derivabila partial in punctual a si atunci considerand F=(f₁,f₂,.,f_m), unde f_i:DR, i=, functiei F ii putem asociem o matrice care contine pe linia i derivatele partiale ale functiei f_i , i=, in raport cu cele n variabile.

Matricea asociata lui F are urmatoarea forma:

J_F(a)=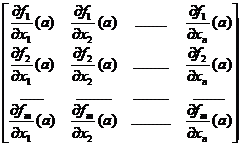

si se numeste matricea jacobiana a lui F in punctul a, dupa numele matematicianului german C.G.Jacobi.Se observa ca J_F(a) este o matrice de tip mn.

Tinand seama de faptul ca F=(f₁,f₂,.,f_m) - diferentiabila in punctual af_i -diferentiabila in a si dF(a)=(df₁(a),df₂(a),..,df_m(a)) (cf. th. 3) iar

df_i(a)()=, i=, k= (cf.th.9)

matricea atasata operatorului liniar T=dF(a):RⁿR^m in bazele canonice e₁,e₂,.,e_nRⁿ si e'₁,e'₂,..,e'_m R^m este tocmai matricea jacobiana in punctual a.

Definitia7

Numim izomorfism liniar intre spatiul X si Y o aplicatie liniara de la X la Y, care este bijectiva.

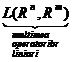
Functia :Mmn asociaza fiecariu operator liniar TL(Rⁿ,R^m) matricea A_T in bazele canonice, este un izomorfism liniar.

Utilizand izomorfismul liniar putem identifica, diferentiala functiei F in punctul a cu matricea jacobiana J_F(a).

Daca m=n J_F(a) - este o matrice patratica.Determinantul ei se numeste jacobianul (determinantul functional) al functiilor f₁,f₂,.,f_n in punctual a si vom nota= detJ_F(a)

Ex1.

Fie functia F:DR² , unde D este un deschis din [0,∞)R, definite prin

F( D.

Observam ca F este diferentiabila pe D intrucat functiile f₁( si f₂( sunt diferentiabile pe D.

Matricea jacobiana a lui F in punctual current va fi

J_F(

iar jacobianul va fi detJ_F(

Functia F exprima legatura intre coordonatele carteziene si coordonatele polare, in R².

Ex2.

Fie F:DR³, unde D este un deschis din [0,∞)R², definite prin

F( D.

Observam ca F este diferentiabila pe D intrucat functiile

f₁( , f₂( ,f₃( sunt diferentiabile pe D.

Matricea jacobiana a lui F in punctual curent va fi:

J_F(

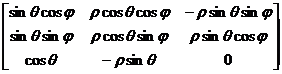
Iar jacobianul va fi detJ_F(

Functia F de mai sus exprima legatura intre cordonatele carteziene si coordonatele polare in R³.

Teorema12

Daca F:DRⁿ diferentiabila pe D, unde este un deschis din Rⁿ,atunci in aD matricea jacobiana J_F(a) este nesingulara dF(a) este un izomorfism liniar.