|
|
|
ARHIMEDE (287-212 I.E.N.)
-
METODA
- PARABOLA
- SFERA SI CILINDRUL
- CONOIZII SI SFEROIZII
- CORPURILE PLUTITOARE
- SPIRALELE
- MASURAREA CERCULUI
- NUMERATIA: ARENARIUM
Se povesteste ca Arhimede din Siracuza a fost ucis de un soldat,
la virsta de 75 de ani, in anul
Lista scrierilor lui care au ajuns pana la noi cuprinde, intr-o ordine pe cat
posibil cronologica, urmatoarele:
1. Prima carte Despre echilibrul planelor.
2. Memoriul: Cvadratura parabolei.
3. A doua carte Despre echilibrul planelor.
4. Cele doua carti Despre sfera si cilindru.
5. Tratatul Despre spirale.
6. Tratatul Despre conoizi si sferoizi.
7. Cele doua carti Despre corpurile plutitoare.
8. Masurarea cercului.
9. Arenarium (problema numararii firelor de nisip).
10. Scrisoarea catre Eratostene Despre metoda, un fel de testament stiintific,
in care Arhimede dezvaluie, in parte, secretul descoperirilor sale.
O culegere de leme tradusa din araba este, in forma ei actuala, fara indoiala,
apocrifa. Ea contine totusi propozitii, elegante insa elementare, care
figureaza, probabil, in unele din operele pierdute.
De altfel, Pappus da destul de multe detalii despre cele 13 poliedre
semiregulate inventate de Arhimede. Lui Arhimede i se mai atribuie si o
epigrama, asa-numita "problema
a taurilor lui Helicon", care conduce la ecuatia nedeterminata, in numere
intregi: 
,
unde, in plus, trebuie sa fie divizibil cu 9314. Pentru a scrie in sistemul
nostru de numarare valorile cele mai mici ale numerelor cautate, ar fi nevoie
de 744 de pagini dintr-o lucrare de formatul 14x33 cm2 ,
continand 2600 de cifre pe fiecare pagina. Bineinteles, Arhimede da numai
enuntul.
METODA. Scrisoarea catre
Eratostene, care a fost gasita abia in 1907, ne da cheia principalelor
descoperiri ale lui Arhimede. Gratie ei si folosind dispunerea in ordine
cronologica a memoriilor, realizata cu ajutorul prefetelor, ne putem face o
reprezentare aproximativa a mersului gandirii acestuia.
Familiarizat cu legile staticii aplicate (nu trebuie uitat ca, pe vremea aceea,
Siracuza era in avangarda progresului tehnic), Arhimede admite existenta unui
centru de greutate la toate corpurile grele si in prima carte Despre echilibrul planelor incearca o reconstituire logica a
acestor legi, pornind de la un numar minim de postulate. Atitudinea lui
matematica se manifesta clar inca de aici. El nu aplica, in general, matematica
la tehnica; din contra, tehnica este inspiratoarea lucrarilor lui teoretice.
Dupa ce stabileste legea parghiei, el trece la studiul centrului de greutate al
celor mai simple figuri plane, in particular, al triunghiului.
Aceste cercetari ii inspira cateva reflectii care au deschis matematicii o cale
noua, bogata in perspective. El da explicatii despre noua metoda inca de la inceputul
scrisorii catre Eratostene, ilustrand-o pe exemplul segmentului de parabola,
prima arie careia a reusit sa-i faca exact cvadratura.
In acest rationament prin inductie deosebit de puternic, pe care Arhimede il
utilizeaza in scrisoarea lui si pentru multe alte cvadraturi si cubaturi, doua
sunt faptele deosebit de remarcabile. Primul este utilizarea staticii pentru
descoperiri geometrice; Arhimede nu are prejudecati de purist si se foloseste
de analogii fecunde intre cele doua domenii diferite ale stiintei. Al doilea
este asimilarea ariei cu o suma de segmente rectilinii, a volumului cu o suma
de sectiuni plane si, in general, asimilarea unui continuu cu suma unui numar
infinit de entitati indivizibile.
Cavalieri va relua aceasta cale in secolul al XVII-lea si metoda se va dovedi
la fel de fecunda, insa subtilul italian va ramane, intr-o anumita masura,
prizonierul propriei sale descoperiri si nu va reusi sa completeze analiza
intuitiva facuta de el cu o sinteza riguroasa. Precursorul lui reusise insa, in
mod elegant, sa depaseasca acest pas dificil, ceea ce ne da o proba manifesta
de amploarea geniului lui Arhimede.
PARABOLA. Intr-adevar, in Cvadratura parabolei, el
elimina succesiv cele doua dificultati. Intr-o prima demonstratie, el pastreaza
acelasi desen din scrisoarea catre Eratostene, dar nu mai descompune segmentul
de parabola intr-o infinitate de drepte. Din contra, el inscrie in segment si
circumscrie acestuia doua serii de trapeze. Efectuand rationamentul potrivit
metodei sale, el arata, in continuare - facand apel la exhaustiunea lui Eudoxos
- ca aria segmentului nu poate fi nici mai mare, nici mai mica decat o treime
din aria triunghiului.
Insa aceasta demonstratie riguroasa ramane inca tributara principiilor staticii
si nu-l satisface complet pe Arhimede. De aceea, el da o demonstratie strict
geometrica in care urmareste pas cu pas demonstratia folosita de Eudoxos la
cubatura piramidei:
ABC este segmentul de parabola, C este punctul in care tangenta este paralela
Seria 
avand
ca limita 4/3 , Arhimede arata ca segmentul
nu poate fi nici mai mic, nici mai mae decat 4/3 din triughiul ABC.
In cartea a doua Despre
echilibrul planelor, Arhimede
cauta centrul de greutate al segmentului de parabola. Demonstratia este facuta
in mai multe etape. Ea se bazeaza pe inscrierea in segmentul de parabola a
seriei de triunghiuri folosite deja la cvadratura geometrica. Se stabileste mai
intai, printr-un rationament prin exhaustiune, ca centrul de greutate se afla
pe diametrul segmentului. Propozitia a 5-a arata apoi ca el este mai aproape de
varful segmentului decat centrul de greutate al figurii inscrise. Demonstratia,
ca atare, este remarcabila: ea constituie primul exemplu, cunoscut cu
certitudine, de rationament prin inductie completa sau prin recurenta (cu
conditia, bineinteles, ca puristii moderni sa accepte sa ierte grecilor ca nu
si-au formulat demonstratiile dupa toate canoanele cuvenite). Se demonstreaza
apoi ca distanta dintre cele doua centre de greutate poate fi facuta oricat de
mica dorim si dupa aceea ca centrele celor doua segmente de parabola impart
diametrele respective intr-un acelasi raport care, dupa legile staticii, are
valoarea 3/2.
SFERA SI CILINDRUL. In
scrisoarea catre Eratostene, Arhimede expune rationamentul prin care statica
i-a permis sa gaseasca raportul dintre sfera si cilindrul circumscris. El
adauga:
"Examinarea acestei propozitii m-a condus la ideea ca suprafata oricarei
sfere este egala cu patru cercuri mari ale sferei. Intr-adevar, am admis ca,
dupa cum cercul este echivalent cu triunghiul care are ca baza circumferinta
cercului si ca inaltime raza acestuia, tot asa sfera este echivalenta cu conul
care are ca baza suprafata sferei si ca inaltime raza."
Prima dintre cele doua carti Despre
sfera si cilindru - una
dintre operele cele mai celebre ale siracuzanului - este consacrata tocmai
stabilirii riguroase a acestor rezultate. Ea debuteaza cu enuntul urmatoarelor
postulate:
"1. Dreapta este linia cea mai scurta care ii uneste extremitatile.
2. Daca doua linii plane, convexe, care unesc doua puncte date, sunt situate de
acceasi parte a dreptei care uneste aceste puncte, iar una dintre linii o
cuprinde pe cealalta, linia care cuprinde este cea care este mai mare.
3. Tot asa, dintre toate suprafetele care au aceleasi limite, planul este
suprafata minima, daca limitele sunt plane.
4. Daca dintre doua suprafete care sunt limitate de un acelasi plan si sunt
situate de acceasi parte a planului, una infasoara pe cealalta, infasuratoarea
are suprafata mai mare."
5. Postulatul lui Arhimede, asa cum l-am formulat mai sus.
Dupa Arhimede, si inca din antichitate, postulatele 1 si 3 au fost deseori
considerate drept definitiile dreptei si respectiv, planului, ca de exemplu in
Definitiile atribuite lui Heron din Alexandria. Incepand cu editia Euclid,
datorata lui Campanus (secolul al XIII-lea), dreapta a fost deseori definita in
special in invatamantul francez ca fiind drumul cel mai scurt.
Pe baza celor 5 postulate si folosind un rationament subtil prin exhaustiune,
geometrul stabileste mai intai ca suprafata laterala a unui con sau a unui
cilindru drept este mai mare decat cea a piramidei sau a prismei inscrise, dar
mai mica decat aria laterala a piramidei sau a prismei circumscrise. De aici el
obtine, in continuare, valoarea ariei laterale a conului si a cilindrului
drept, exprimata, bineinteles, nu prin formule sau canoane care fac apel la
calcule, ci in comparatie cu ariile cercurilor. In epoca aceea, canoane de
felul acesta existau numai in geodezie si in geometria aplicata. In
invatamantul elementar s-a pastrat, in mare - mai putin rigurozitatea - mersul
rationamentelor care conduc de aici la aria si volumul sferei.
A doua carte Despre
sfera si cilindru rezolva
diferite probleme folosind metodele algebrei. Cand este vorba sa se gaseasca
sfera care are acelasi volum ca un con sau un cilindru dat, Arhimede reduce
rezolvarea la problema inscrierii a doua medii iproportionale intre doua
lungimi date. Vom vedea ceva mai tarziu ca Apollonios va proceda la fel in
Cartea a V-a din Conice.
Asadar, pentru ambii - deoarece nici unul nici altul nu fac nici cel mai mic
comentariu cu privire la operatia folosita - inserarea celor doua medii
proportionale era o problema banala, cunoscuta la perfectie de toata lumea. Pe
ei nu-i deranjeaza catusi de putin faptul ca problema nu este rezolvata cu
ajutorul riglei si compasului.
Informatiile cele mai precise cu privire la aceasta problema celebra le datoram
comentariului lui Eutokios la tratatul lui Arhimede.
Pentru a sectiona o sfera, printr-un plan, in doua segmente ale caror volum
sunt intr-un raport dat, geometrul propune sa se imparta un segment AB
printr-un punct X, astfel incat raportul dintre AX si o lungime data sa fie
egal cu raportul dintre o arie data si patratul lui XB, adica
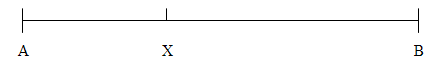
El promite sa se ocupe mai tarziu de aceasta problema noua despre care
semnaleaza ca, in general, are o "limitare" - un "diorism" - insa nu ne-a
parvenit nimic din lucrarea promisa. Tacerea lui Arhimede este rascumparata in
parte de Eutokios, care formuleaza mai multe solutii obtinute prin intersectarea
conicelor, printre care si una pe care o considera ca apartine in intregime
siracuzanului.
Pe de alta parte, tinand seama de polemicele contemporane lui Arhimede dintre
matematicienii de
Arhimede face din nou aluzie la aceasta problema in tratatul Despre conoizi si
sferoizi. Astazi, problema s-ar exprima printr-o ecuatie de gradul al treilea
de un tip foarte bine studiat. In fine, ultima propozitie este un caz de
"diorism" sau de "determinare"; ea stabileste ca dintre toate segmentele
sferice care au aceeasi arie semisfera are volumul maxim.
CONOIZII SI SFEROIZII. In
cartea Despre conoizi si
sferoizi isi fac aparitia
trei noi corpuri de revolutie. Sferoidul este generat prin rotirea unei elipse
in jurul uneia dintre axe si este "turtit", daca axa de rotatie este axa mica a
elipsei, si "alungit", cand rotatia se face in jurul axei mari. Conoidul
obtuzunghic se obtine prin rotirea ramurii de hiperbola un jurul axei
transversale, iar conoidul drept - prin rotirea parabolei in jurul axei
proprii. Arhimede, care, in scrisoarea catre Eratostene, calculeaza raportul
dintre volumele acestor corpuri si volumele conurilor folosind procedeele sale
de statica si stabileste pozitiile centrelor de greutate ale segmentului de
conoid dreptunghic, semisferei, segmentului sferic, segmentului de sferoid si
conoidului obtuzunghic, isi propune aici sa compare volumele prin procedee pur
geometrice.
Metoda lui de calcul capata acum o forma care se apropie, in mod surprinzator,
de calculul integral modern. El insereaza volumele de studiat intre doua serii
de cilindri, prima - formata din cilindri inscrisi, a doua - din cilindri
circumscrisi. Deoarece cele doua volume totale ale seriilor de cilindri nu
difera decat prin volumul ultimului cilindru din serie, diferenta dintre ele
poate fi facuta arbitrar de mica. Pentru a ajunge la formulele finale, Arhimede
foloseste inegalitatile:
si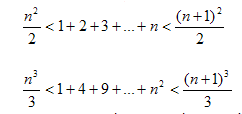 
In esenta, se poate spune ca, in aceasta lucrare, Arhimede a ajuns la conceptul
de integrala definita. Metoda statica folosita mai inainte ii sugerase
principiul descompunerii in straturi paralele. Aici insa, principiul acesta
este eliberat de consideratiile straine de geometrie si, pe de o parte, este
imbinat cu algoritmul seriilor numerice pe care il punea la dispozitie traditia
numerelor figurative, iar pe de alta parte, datorita metodei de exhaustiune a
lui Eudoxos, este inzestrat cu o structura riguroasa care trebuia sa-i asigure
din plin forta sa doveditoare.
CORPURILE PLUTITOARE. In
prima carte a lucrarii Despre
corpurile plutitoare, Arhimede pune bazele hidrostaticii. Lagrange in Mecanica analitica, da un
excelent rezumat al acelei lucrari:
"Arhimede formuleaza urmatoarele doua principii pe care le considera drept
principii experimentale si pe care isi fundamenteaza intreaga teorie: 1. Natura
fluidelor este astfel, incat partile mai putin apasate sunt impinse de cele
care sunt apasate mai mult, iar fiecare parte este totdeauna apasata de
intreaga greutate a coloanei verticale de fluid care ii corespunde; 2. Tot ceea
ce este impins in sus de catre un fluid este impins totdeauna dupa
perpendiculara care trece prin centrul lui de greutate.
Din primul principiu, Arhimede trage mai intai concluzia ca suprafata unui
fluid ale carui parti sunt presupuse ca apasand toate catre centrul Pamantului,
trebuie sa fie sferica, pentru ca fluidul sa fie in echilibru. Dupa aceea, el
demonstreaza ca un corp la fel de greu ca un volum egal de fluid trebuie sa se
cufunde complet, pentru ca, daca consideram doua piramide egale din fluidul
presupus in echilibru in jurul centrului Pamantului, cea in care corpul nu s-ar
scufunda decat in parte ar exercita o presiune mai mare decat cealalta asupra
centrului Pamantului sau, in general, asupra unei suprafete sferice oarecare pe
care ne-o imaginam in jurul acestui centru. El dovedeste in felul acesta ca
corpurile mai usoare decat un volum egal de fluid nu se pot cufunda decat pana
ce partea cufundata ocupa locul unui volum de fluid la fel de greu ca intregul
corp; de aici el deduce urmatoarele teoreme ale hidrostaticii: corpurile mai
usoare decat volume egale din fluidul in care sunt cufundate sunt impinse de
jos in sus cu o forta egala cu excesul greutatii fluidului dislocat asupra
greutatii corpului cufundat, si corpurile mai grele pierd din greutatea lor o
parte egala cu cea a fluidului dislocat."
Arhimede se foloseste apoi de-al doilea principiu formulat de el pentru a
stabili legea echilibrului corpurilor care plutesc. El demonstreaza ca orice
segment de sfera mai usor decat un volum egal de apa, care este cufundat in
apa, trebuie, in mod necesar, sa se dispuna astfel, incat baza lui sa fie
orizontala. Demonstratia data de Arhimede arata ca daca baza ar fi inclinata,
greutatea portiunii exterioare lichidului, considerata concentrata in centrul
de greutate a acesteia impeuna cu impingerea verticala a lichidului,
considerata de asemenea ca fiind concentrata in centrul de greutate al partii
cufundate, ar tinde totdeauna sa roteasca corpul pana ce baza acestuia ar
deveni orizontala.
In cartea a doua, Arhimede aplica acelasi principiu la echilibrul unui segment
de "conoid dreptunghic" sau, folosind terminologia actuala, al unui segment de
paraboloid de revolutie. Inca de la inceputul acestei carti, se admite in mod
tacit ca suprafata apei este un plan orizontal si ca verticalele sunt drepte
paralele. Arabescurile stralucite in jurul noii teme care constituie continutul
acestei carti nu urmaresc vreun scop utilitar; ele nu sunt decat exercitii
indraznete si elegante intreprinse exclusiv pentru placerea creatorului lor si
a cititorilor capabili sa le inteleaga.
SPIRALELE. Tratatul Despre spirale este consacrat studiului unei curbe
definite cinematic: spirala lui Arhimede.
Toata partea acestui memoriu care se refera la cvadraturi este tratata in
acelasi spirit ca si lucrarea Despre
conoizi si sferoizi. Merita sa ne oprim asupra problemei determinarii
tangentelor, deoarece, in privinta aceasta, lucrarea constituie cel mai vechi
tratat de calcul diferential.
Pentru matematicienii greci, o curba se obtine cu ajutorul miscarii unui punct:
un prim exemplu il constituie definitia spiralei. Alte exemple ne sunt oferite
de cvadratricea lui Hippias (sau a lui Dinostrates) si de elicea cilindrica a
lui Apollonios. Un alt exemplu care dateaza din secolul al IV-lea figureaza in
solutia data de Archytas problemei celor doua medii proportionale, asa cum ne-o
relateaza Eutokios dupa o marturie a lui Diogene Laertiu: "Archytas a fost primul care a
folosit miscarea in rezolvarile si descrierile geometrice.". Este adevarat
ca Apollonios descrie conicele ca sectiuni plane printr-un con, dar suprafata
conului este ca insasi definita, in prealabil, prin miscarea continua a unei
linii drepte. Pe de alta parte, in toate textele grecesti cunoscute, o curba
plana inseamna frontiera - sau o parte din frontiera - dintre doua regiuni ale
planului, dintre care una, "figura", nu poate contine decat segmente de
dreapta, dar nu si drepte intregi, nelimitate, si este, in general, un domeniu
convex.
Tangenta la curba intr-unul dintre punctele acesteia este atunci o dreapta
infinita, care trece prin acel punct si ramane exterioara figurii cel putin in
vecinatatea punctului. O astfel de conceptie impune insa nu numai demonstrarea
existentei tangentei intr-un punct al curbei dar, in cazul existentei acesteia,
si a unicitatii ei. Aceasta a doua parte a demonstratiei consta in a arata ca
oricare alta dreapta, diferita de tangenta, care trece prin punctul de contact,
sectioneaza in mod necesar figura. Cei trei mari matematicieni greci care au
tratat problema si ale caror scrieri au ajuns pana la noi - Euclid pentru cerc,
Apollonios pentru conice si Arhimede pentru spirala care-i poarta numele - au
procedat exact asa si cu aceeasi scrupulozitate.
Antichitatea s-a ocupat si de curbe strambe, dar nu dispunem de nici un text
are sa faca aluzie la tangentele la astfel de curbe.
Arhimede trece sub tacere analiza care i-a permis sa gaseasca tangenta la
spirala lui, insa aici, partea delicata rezida nu in aceasta analiza, ci in
sinteza pe care el o expune cu mana de maestru. Este relativ usor de demonstrat
ca dreapta presupusa tangenta este, intr-adevar, exterioara figurii, insa este
mult mai dificil de stabilit ca ea este singura care se bucura de aceasta
proprietate. Rationamentul lui Arhimede vadeste aici o frumoasa eleganta
geometrica, insa ca de obicei, marele matematician pretinde foarte multe din
partea cititorului. Pentru a demonstra propozitia, Arhimede inlocuieste o
problema transcendeta prin alte doua probleme, care sunt algebrice si de grad
mai mare decat 2. Acestea sunt asa-numitele intercalari, cazuri particulare de
neusis. El se opreste aici si lasa pe seama cititorului discutia acestor
probleme pe care o considera banala. Pappus ii reproseaza acest fapt, insa este
usor sa i se dea satisfactie, inlocuindu-le, la randul lor, prin altele de
gradul I; este tocmai ceea ce se face astazi, in mod curent, in calculul
diferential.
Arhimede enunta, in prefata, rezultatul esential al studiului sau: "Daca o dreapta este
tangenta la spirala in punctul care este ultima extremitate a acesteia si daca
pe dreapta care s-a rotit pana ce si-a reluat locul se ridica o perpendiculara
pe extremitatea fixa a acesteia, pana la intalnirea cu tangenta, spun ca
dreapta astfel dusa pana la intersectie este egala cu circumferinta cercului".
MASURAREA CERCULUI. Se poate
spune ca memoriul Despre spirale face parte din cercetarile teoretice cu
privire la rectificarea circumferintei cercului. Cat priveste micul tratat
despreMasurarea cercului el
face parte din cercetarile cu caracter practic referitoare la aceeasi problema.
El constituie un frumos exemplu de geodezie greaca sau de geometrie practica.
Se stie ca, pentru egipteni, cercul era echivalent cu un patrat cu latura cat
8/9 din diametru. Aceasta revine la a adopta pentru π valoarea 
.
Babilonienii, in calculele lor mai precise, admiteau aproximatia 
(in numeratia sexagesimala) adica 31/8.
Desi nu ne-a ramas nici un document, este de presupus ca grecii, in cursul
diferitelor tentative de cvadratura, au fost condusi sa adopte valori care erau
apropiate de cele de mai sus si a caror exactitate era mai mult sau mai putin
bine stabilita.
Micul tratat al lui Arhimede arata, in prima propozitie, ca in cazul cercului,
problema cvadraturii este echivalenta cu problema rectificarii circumferintei.
Mai exact, el stabileste, prin metoda exhaustiunii, ca cercul este echivalent
cu triunghiul dreptunghic care are una dintre laturile unghiului drept egala cu
raza, iar cealalta latura egala cu circumferinta. A doua propozitie stabileste
ca daca circumferinta este 
din diametru, cercul este 11/4 din patratul
acestuia. In fine, a treia propozitie demonstreaza, in mod riguros, ca
circumferinta este cuprinsa intre
din diametru, cu alte cuvinte, ca
aceasta ultima valoare, atat de simpla, este o aproximatie prin exces,
imprecizia ei fiind, grosso modo, mai mica decat 1/500.
Punctul slab al logisticii grecesti, arta calculului, consta in secolul al
III-lea, in absenta fractiilor sistematice. In secolul al II-lea, astronomii au
facut apel la fractiile sexagesimale babilonene, conferind acestora o
perenitate cvasiabsoluta, deoarece le mai folosim si azi pentru masurarea
unghiurilor si a timpului. In acest tratat, Arhimede foloseste in calcule numai
fractiile obisnuite.
El o face, ca de obicei, cu o mana de maestru, fara insa sa dea nici cea mai
mica explicatie de detaliu. Astfel, fara sa clipeasca, el adopta 
pentru
valoarea prin exces 1351/780 si valoarea prin lipsa 265/153. Ambele valori sunt
excelente, ele reprezentand reduse ale dezvoltarii lui in fractie
continua.
NUMERATIA: ARENARIUM. Ultimul
tratat care ne-a ramas de examinat, Arenarium, se refera la logistica numerelor
intregi, adica la numeratie.
Grecii utilizau doua procedee de scriere a numerelor. Primul, sistemul atic,
numit uneori si herodian, era analog sistemului roman care s-a pastrat pana in
zilele noastre. Literele I, II, Δ, H, X, M reprezentau, respectiv,
numerele 1, 5, 10, 100, 1000 si 10000.
Ca si sistemele analoge lui, sistemul atic nu se putea preta la calcule cat de
cat complicate (asa cum s-a intamplat ulterior si cu sistemul latin). Aceste
calcule necesitau utilizarea tablelor socotitoare sau a abacelor, pe care se
manipulau jetoane.
Insa probabil de pe la mijlocul secolului al V-lea si, mai ales, incepand din
secolul al III-lea, grecii au inceput sa utilizeze, intre altele, si o savanta
numeratie scrisa, semipozitionala si zecimala, bazata pe principiul urmator:
primele 9 litere ale alfabetului grecesc reprezentau primele 9 numere; alte 9
litere reprezentau primele 9 zeci si, in fine, urmatoarele 9 litere - primele 9
sute. Petru mii se lua alfabetul de la inceput, insa jos, in stanga literei, se
plasa un indice.
In decursul timpului, numeratia aceasta a suferit mai multe modificari. De
exemplu,
Arhimede isi propune sa elaboreze mai departe acest sistem de numarare - mai
putin practic decat cel folosit de noi, insa foarte comod in calcule - pentru
a-i permite sa reprezinte numere extrem de mari.
El reuseste, in cele din urma, sa enunte un numar egal cu 
,
adica unu urmat de 800 de milioane de zerouri, si ilustreaza procedeul imaginat
de el, calculand un numar mai mare decat numarul grauntilor de nisip care ar
putea fi continuti in sfera stelelor fixe. Arhimede foloseste aceasta problema
drept pretext pentru a expune succint sistemul astronomic al lui Aristarh din
Samos.
Calea indicata de Arhimede pentru a ajunge la scrierea numerelor foarte mari
n-a fost urmata; s-a preferat o cale mai simpla, datorata lui Apollonios si
care foloseste o progresie in miriade.
Completata in astronomie prin adoptarea fractiilor sexagesimale, numeratia savanta
a grecilor a fost instrumentul pe care l-au folosit toti calculatorii, in
special astronomii, pana la introducerea cifrelor asa-zise arabe, pe care le
folosim noi. Chiar si dupa adoptarea de catre matematicienii arabi a
aritmeticii de pozitie, compatriotii lor, astronomii, au ramas mult timp fideli
procedeului grecesc, adaptat alfabetului arab. In schimb, in Occident, dupa
ruptura de Imperiul de rasarit, gasim exemple de calcule efectuate in
continuare, cu ajutorul penibilei numeratii latine.
B i b l i o g r a f i e:
"ISTORIA GENERALA A STIINTEI"
Publicata sub conducerea lui Rene Taton
Vol. I Stiinta antica si medievala de la origini la 1450
