
|
|
|
1 Prezentare
In anumite aplicatii, datele nu se descompun logic in inregistrari independente, asupra carora sa se poata aplica metodele de cautare clasice. O astfel de clasa de aplicatii este identificarea (cautarea) sirurilor de caractere. In acest tip de aplicatii se prelucreaza un sir de caractere, numit sir text in care se cauta prima aparitie sau toate aparitiile unui subsir, numit sablon.
Literatura de limba engleza foloseste termenii pattern pentru sablon, match pentru identificare si no match pentru nepotrivire.
Caracterele fac parte dintr-un alfabet finit A. Dimensiunea alfabetului din care este construit sirul este un factor important in proiectarea algoritmilor de indentificare.
Printre aplicatiile practice ale prelucrarii sirurilor se numara: editarea textelor (sir text), prelucrarea imaginilor (sir binar), muzica (sirul este format din reprezentari ale notelor muzicale) si, in general, orice recunoastere de obiecte care pot fi codificate prin simboluri (unghiuri de poligoane, perechi de baza de acizi DNA, partile unui ansamblu mecanic, etc).
Identificarea (recunoasterea) sabloanelor este o operatie de baza asupra sirurilor. Fiind dat un text de forma T = t1t2t3tN, unde N este lungimea sirului, si un sablon P = p1p2p3pM, de lungime M, sa cere sa se gaseasca o aparitie a sablonului in text, adica se cere gasirea pozitiei i (pentru prima aparitie) sau a multimii de pozitii i (pentru toate aparitiile), astfel incit ti+j = p1+j, cu 1 i N-M+1.
Algoritmii prezentati se refera la gasirea primei aparitii a sablonului, dar pot fi extinsi cu usurinta la gasirea tuturor aparitiilor, deoarece fac o trecere secventiala prin text si pot porni din nou dupa gasirea primei aparitii a sablonului.
Observatie: Problema "identificarii sabloanelor" poate fi vazuta si ca o problema de cautare, unde cheia este sablonul, dar algoritmii de cautare clasici nu se pot aplica, deoarece sablonul poate fi lung si poate sa se "alinieze" oriunde in text.
2 Scurt istoric al algoritmilor de recunoastere a sabloanelor
1. Algoritmul fortei brute. Are un timp al cazului cel mai nefavorabil proportional cu N*M, dar in multe cazuri practice, timpule mediu este proportional cu N+M.
In 1970, S.A. Cook a demonstrat teoretic, folosind un model de masina abstracta, ca exista un algoritm de identificare a sabloanelor cu timpul cel mai nefavorabil proportional cu N+M. Pornind de la modelul lui Cook, D.E. Knuth si V.R. Pratt au construit un astfel de algoritm. In acelasi timp, J.H. Morris a descoperit acelasi algoritm in timpul implementarii unui editor de texte, din dorinta de a nu se mai intoarce in text dupa aparitia unei nepotriviri.
3. R.S. Boyer si J.S. Moore au descoperit, in 1976, un algoritm chiar mai rapid decit (2) in multe aplicatii, deoarece examineaza in multe cazuri numai o parte din caracterele textului. Multe din editoarele de texte moderne folosesc acest algoritm pentru eficienta.
Observatii:
Algoritmul KMP se bazeaza pe teoria automatelor finite si are avantajul ca nu se intoarce niciodata in sirul text, deci este foarte potrivit pentru cazul in care cautarea se face pe un mediu extern. El imbunatateste performantele cazului cel mai nefavorabil.
Algoritmul BM se bazeaza pe ideea ca alfabetul este finit (exploateaza aceasta idee), imbunatateste timpul mediu, dar se intoarce in sir (de fapt nu se intoarce sa compare din nou, dar merge si de la dreapta la stinga in sir, nu numai de la stinga la dreapta).
4. In 1980, R.M. Karp si M.O. Rabin au observat ca problema identificarii sabloanelor nu este mult diferita de o problema standard de cautare si au descoperit un algoritm aproape la fel de simplu ca cel al fortei brute, dar care are virtual intotdeauna timpul proportional cu M+N. In plus, algoritmul lor se extinde cu usurinta la un sir si un sablon in doua dimensiuni (util in prelucrarea imaginilor).
3 Algoritmul cautarii directe
Ideea de baza a acestei metode este sa se verifice, pentru fiecare pozitie din text, daca apare sau nu sablonul. Exemplul de mai jos cauta prima aparitie a sablonului p in sirul a si intoarce pozitia sablonului in text, daca p a, sau N in caz de nepotrivire.
int cautsablon1(char *p, char *a)
if (j==M) return i-M;
i-=j-1;
j = 0;
} while (i<N);
return i;
}
Comentariu: Se fac doua teste in bucla interioara si un test in cea exterioara. Se poate elimina testul (i < N) din bucla interioara daca se introduce o santinela: la sfirsitul lui a se adauga p, astfel ca p sa fie intotdeauna gasit. Daca valoarea intoarsa este N (lungimea lui a inainte de adaugarea santinelei) atunci p nu este cuprins in a.
O alta varianta a aceluiasi algoritm este prezentata in continuare.
int cautsablon2(char *p, char *a)
if (j==M)
return i-M;
else
return i;
}
Comentarii:
(a) Cit timp i si j desemneaza caractere egale, i si j sint incrementati. Daca cele doua caractere sint diferite, j se reseteaza la inceputul sablonului, iar i se deplaseaza cu o pozitie la dreapta fata de cea din care s-a inceput comparatia (i = i-j+1).
(b) Se introduce santinela p la sfarsitul lui a.
(b) Daca s-a ajuns la sfirsitul sablonului (j==M), atunci a aparut identificarea pe pozitia a[i‑M]; altfel, inseamna ca s-a ajuns la sfirsitul sirului si se intoarce N (pe post de santinela, semnificind no-match).
In multe aplicatii de prelucrare a textelor, bucla interioara se executa rareori si timpul de rulare este proporional cu N+M. Daca sablonul are insa multe caractere comune cu textul, deci exista multe starturi false, performantele se inrautatesc.
Proprietate: Algoritmul fortei brute necesita, in cazul cel mai nefavorabil, un numar de maxim N*M comparatii de caractere.
Cazul cel mai nefavorabil poate apare, de exemplu, la prelucrarea imaginilor binare. Daca atit textul, cit si sablonul sint siruri de 0 urmate de siruri de 1, atunci, pentru fiecare din cele N-M+1 pozitii de identificare, toate caracterele din sablon sint comparate cu sirul. Rezulta ca timpul de rulare in acest caz este proportional cu M(N-M+1), si cum M « N obtinem valoarea aproximativa N*M.
4 Algoritmul Knuth-Morris-Prat
Acest algoritm se bazeaza pe urmatoarea idee: cind se detecteaza o nepotrivire intre sir si sablon, falsul start al identificarii consta din caractere deja cunoscute (comparate) si aceasta informatie poate fi utila. Pe baza ei, este posibil ca, dupa detectarea unui fals start, sa nu se mai decrementeze pointerul i din sir.
Pentru a ilustra intuitiv principiul acestui algoritm vom considera urmatorul caz particular: fie un sablon in care primul caracter nu mai apare in restul sablonului, de exemplu 1000000. Sa presupunem ca avem un start fals de j-1 caractere:
sir: 1000001000000
sablon: 1000000
Cind se detecteaza nepotrivirea, pe pozitia j (j==i) se constata ca nu este nevoie ca i sa fie scazut (i=i-j+1), deoarece nici unul din cele j-1 caractere dinaintea celui din pozitia i nu se pot identifica cu primul caracter din sablon. Aceasta schimbare ar putea fi tradusa in program inlocuind i-=j-1 cu i++.
Efectul este insa limitat, deoarece putine sabloane au proprietatea acestui caz particular. Cu toate acestea, autorii algoritmului KMP au demonstrat ca se poate construi un algoritm in care i sa nu fie decrementat, nici chiar dupa un start fals.
Fie urmatoarea situatie:
sir: 1010100111
sablon: 10100111
Nepotrivirea apare la al cincilea caracter (j==4), dar in acest caz nu se poate elimina decrementarea lui i, deoarece este posibila o identificare incepind cu al doilea caracter din sir.
Se poate sti dinainte exact cu cit trebuie decrementat i, deoarece acest lucru depinde de sablon, nu de sirul de intrare. Aceasta dependenta este data caracterele sau grupurile de caractere care se repeta in sablon. Daca nepotrivirea intre sir si sablon apare pe pozitia j in sablon, si exista un k intre 0 si j-2 pentru care p[0] p[k-1] = p[j-k] p[j-1], atunci o posibila identificare intre sir si sablon poate apare incepind cu caracterul (din sir) corespunzator caracterului p[j-k] din sablon. Pentru a nu pierde nici o posibila identificare, trebuie cautat k maxim cu aceasta proprietate. In cazul in care nu exista nici un k pentru care proprietatea este adevarata, atunci cautarea poate fi reluata de la valoarea curenta a lui i (deci de la caracterul care a generat nepotrivirea).
In acest scop trebuie calculate componentele unui vector, numit next[M], in care se memoreaza valoarea cu care trebuie decrementat i cind se detecteaza o nepotrivire a caracterului j din sablon (in next[j]).
Prin definitie, valoarea unui element al vectorului, next[j], reprezinta numarul de caractere next[j] de la inceputul sablonului care se identifica cu ultimele next[j] caractere din sablon, deci este de fapt egala cu kmax care satisface relatia de mai sus.
Cunoscind valorile componentelor vectorului next se stie ca urmatoarea pozitie in sir pentru care sirul poate coincide cu sablonul dupa un start fals (pina la pozitia j in sir) este i-next[j].
4.1 Cum se calculeaza componentele lui next[M]?
In continuare se va da o metoda care este direct legata implementare, iar in finalul prezentarii se va arata cum se pot obtine aceste valori pornind de la modelul formal al unui automat finit determinist care recunoaste un sablon intr-un sir, peste un alfabet dat.
Sa presupunem ca se gliseaza o copie a primelor j caractere din sablon peste sablon, de la stinga la dreapta, incepind cu primul caracter din copie suprapus peste al doilea caracter din sablon. Glisarea se opreste fie cind toate caracterele suprapuse (pina la j-1) coincid, fie cind primul caracter al copiei ajunge pe pozitia j. Procesul ar trebui reluat din aceleasi pozitii (primul caracter al copiei peste al doilea din sablon, apoi suprapus cu al treilea, etc.) pentru fiecare j (incepind de la 1), dar se observa ca se obtine acelasi efect si daca, pentru un anumit j, reluarea se face din pozitia la care a ajuns copia pentru j-1.
j next[j]
1 0 10100111
1
2 0 10100111
10
10
3 1 10100111
101
101 o potrivire
4 2 10100111
1010
1010 doua potriviri
De fiecare data (pentru fiecare j), cautarea ar trebui reluata de la 1. Se observa insa ca este suficienta reluarea de la pozitia anterioara.
5 0 10100111
10100
10100
10100 zero
potriviri
10100
6 1 10100111
101001 o potrivire
7 1 10100111
1010011 o potrivire
1010011
In interpretarea figurii de mai sus trebuie tinut cont de cele spuse anterior, adica:
(1) Pentru un j la care apare o nepotrivire, trebuie cautat kmax, unde 0 k j-2, pentru care exista relatia p[0]p[k-1] = p[j-k]p[j-1]. Urmatoarea pozitie la care sablonul se poate suprapune perfect peste text este i-next[j].
(2) Prin definitie, primele next[j] caractere din sablon coincid cu ultimele next[j] caractere de la stinga lui j.
Caracterele suprapuse perfect (identice) definesc urmatorul loc posibil in care sablonul se poate identifica cu sirul, dupa ce se gaseste o nepotrivire pe pozitia j (caracterul p[j]). Distanta cu care trebuie sa ne intoarcem in sir este exact next[j], adica numarul de caractere care coincid. Dupa cum se va vedea in continuare (in program), este convenabil sa i se atribuie lui next[0] valoarea -1.
Cum se poate evita intoarcerea in sir ? Fie i pointer in sir, j pointer in sablon, nepotrivirea a aparut pentru a[i] != p[j], iar testarea a inceput la pozitia i-j+1 in sir. Atunci, dupa cum am aratat, urmatoarea pozitie (in sir) la care sablonul se poate suprapune prefect peste sir este i-next[j].
Dar, prin definitia vectorului next, primele next[j] caractere din pozitia i-next[j] in sir coincid cu primele next[j] caractere din sablon. Rezulta deci ca nu trebuie decrementat i, ci se poate atribui lui j valoarea next[j].
Exemplu:
sir: 1010100111 (i=4)
sablon: 10100111 (j=4)
Compararea ar trebui reluata astfel:
1010100111 (i'=i-2)
10100111 (j'=0, next[4]=2)
Este suficient totusi daca se continua ca mai jos:
1010100111 (i'=i)
10100111 (j'=2)
4.2 Cautarea sablonului
int cautKMP(char *p, char *a)
Comentarii:
a) Cind j=0 si a[i] nu coincide cu p[0], dorim sa incrementam i si sa tinem j la inceputul sablonului (in bucla for). Acest efect poate fi realizat prin initializarea next[0]= -1, ceea ce duce la j= -1 in bucla while, apoi i incrementat si j=0 in bucla for.
b) Se observa asemanarea cu a doua implementare a algoritmului fortei brute; KMP este avantajos in cazul in care sabloanele au parti repetitive.
4.3 Implementarea calculului tabelei next
Se foloseste programul de mai sus, dar se face identificarea sablonului cu el insusi. Se noteaza cu i pointerul in sablon, cu j pointerul in copia (conceptuala) a sablonului care se translateaza.
void initnext(char *p)
Comentarii:
a) Dupa incrementarea lui i si j, s-a determinat ca primele j caractere ale sablonului coincid cu p[i-j-1], , p[i-1], adica ultimele j caractere ale primelor i caractere din sablon. In plus, acesta este cel mai mare j cu aceasta proprietate (in caz contrar, o posibila identificare a sablonului cu el insusi s-ar fi pierdut) - deci next[i] = j.
b) Algoritmul poate fi imbunatatit in continuare, deoarece nu se ia in considerare caracterul care a generat nepotrivirea. Fie cazul urmator:
sir: 1011 Nepotrivirea apare la al patrulea caracter.
sablon: 10100111
Conform valorilor din vectorul next, compararea ar trebui reluata de al patrulea caracter din sir cu cel de al doilea caracter din sablon. Dar aceste caractere nu pot coincide, deoarece se stie, de la nepotrivire, ca urmatorul caracter din sir nu este 0, asa cum ar trebui sa fie in sablon. In algoritm, acest lucru se exprima inclocuind next[i] = j cu
next[i] = (p[i]==p[j]) ? next[j] : j;
Proprietate: Algoritmul KMP de cautare a sirurilor efectueaza maximum M+N comparatii de caractere.
Aceasta afirmatie se poate deduce din codul C prezentat mai sus: fie se incrementeaza j, fie j devine next[j], cel mult odata pentru fiecare i. In plus, ea se poate demonstra si formal, pornind de la modelul automatului finit care va fi prezentat in continuare.
4.4 Varianta pentru sablon fix
Programul prezentat se poate scrie intr-o maniera foarte eficienta daca se presupune ca sablonul de identificat este fix: vectorul next poate fi "cablat" in program. Urmatoarea varianta este echivalenta cu cea anterioara, pentru sablonul 10100111, dar este mult mai eficienta:
int cautKMP1(char*a)
Comentarii:
a) Secventa de trecere din si in si+1 este data de caracterele din sablon.
b) Etichetele folosite de instructiunile goto sint chiar valorile din tabela next; programul simuleaza de fapt atribuirea corespunzatoare lui j.
c) Pentru a evita verificarea i==N la fiecare incrementare a lui i, se foloseste o santinela (se copiaza sablonul la sfirsitul textului). Atentie! Santinela este obligatorie pentru varianta de mai sus care nu are testul i==N.
d) Acesta este un exemplu simplu de "compilator de siruri": dindu-se un sablon, se poate scrie un program foarte eficient pentru cautarea acelui sablon intr-un sir (text sau binar).
e) Imbunatatirea sugerata la sfirsitul primei implementari (i.e. in loc de next[i]=j, sa se foloseasca next[i] = (p[i]==p[j]) ? next[j] : j ) se poate realiza si in aceasta varianta. Se observa ca, in starea s3, pentru un caracter 1 (!=0) se trece la s1, de unde pentru un 1 (!=0) se trece la s0. Se poate inlocui acest dublu salt cu un salt direct la s0 din starea s3
4.5 Modelul formal al algoritmului KMP
Functionarea programului sugereaza descrierea procesului de identificare a sablonului prin intermediul unui automat finit. De fapt, acesta a fost modelul abstract pe baza caruia Cook a aratat ca timpul de identificare este proportional (in cazul cel mai nefavorabil) cu M+N si modelul de la care au pornit Knuth si Pratt in construirea algoritmului.
Pentru determinarea starii i, automatul are asociata o functie intreaga f, numita functie de esec ("failure function"), cu proprietatea ca f(j) este cea mai mare stare numerotata, mai mica decit sj(j), pentru care p1p2.ps este un sufix al lui p1p2.pj. Aceasta revina la a spune ca f(j) este cel mai mare s < j astfel incit p1p2.ps pj-s+1pj-s+2.pj. Daca nu exista un astfel de s 1, atunci avem f(j) = 0.
Functia f se defineste astfel:
f(1)(j) = f(j)
f(m)(j) = f(f(m-1)(j)), m > 1
Cum foloseste automatul functia f ?
Daca ak+1 pj+1, se aplica repetat functia starii j, pina cind se gaseste cea mai mica valoare pentru care
(a) fie f(m)(j) = u si ak+1 = pu+1, caz in care automatul trece in starea u+1,
(b) fie f(m)(j) = 0 si ak+1 p1, caz in care automatul trece in starea 0.
Am notat cu m cea mai mica valoare pentru care una din relatii este adevarata.
In cazul (a), daca p1p2.pj este cel mai lung prefix al lui p care este un sufix al lui a1a2.ak, este usor de verificat ca (p1p2pf(m)(j)+1) este cel mai lung sufix al lui a1a2.ak+1 In cazul (b) nu exista nici un prefix al lui p care sa fie sufixul lui a1a2.ak+1
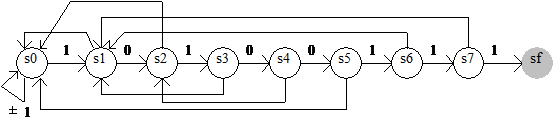
Caracterele din sirul de intrare total diferite de cele din sablon sint citite numai in s0, pe tranzitia s0 p--> s0, p p0. Automatul citeste un nou caracter de intrare numai pentru tranzitiile "la dreapta", i.e. cind caracterul din sir se potriveste cu sablonul; altfel automatul se intoarce fara a citi un nou caracter (acesta este motivul pentru care nu sint etichetate si tranzitiile "la stinga"). Si in acest automat se poate face imbunatatirea din program.
Din punct de vedere al teoriei automatelor, detectarea aparitiei unui sablon p = p1p2.pl in sirul a1a2.an poate fi reprezentata printr-un automat finit determinist construit asa cum se descrie in continuare.
Se construiesc l+1 stari s0, s1, . sl, unde l este lungimea sablonului si cite o tranzitie din si-1 in si pentru un simbol de intrare pi. Starea s0 are o tranzitie spre ea insasi pentru orice caracter diferit de p1 O stare si poate fi vazuta ca starea in care pointerul in sablon indica spre caracterul pi. O stare si corespunde prefixului p1p2.pi al sablonului.
Sa presupunem ca, dupa ce a citit din sir caracterele a1a2.ak, automatul este in starea sj. Aceasta implica faptul ca ultimele j caractere ale secventei a1a2.ak sint p1p2.pj si ca ultimele m caractere ale secventei a1a2.ak nu sint un prefix al lui p1p2.pl, pentru m > j.
Daca ak+1 = pj+1, atunci automatul trece in starea sj+1(j+1) si avanseaza pointerul in sir la ak+
Daca ak+1 pj+1, automatul intra in starea si, cu i cel mai mare numar pentru care p1p2.pi este un sufix al lui a1a2.ak+1; daca nu exista nci un astfel de sufix, automatul trece in starea s0
Exemplu
p = AABBAAB
i
1
2
3
4
5
6
7
f(j)
0
1
0
0
1
2
3
Se observa ca f are valorile vectorului next.
O schita a calculului functiei f avind modelul automatului, cu sablonul p1p2.pM si starile numerotate de la 0 la M, este:
f(1) 0
for j 2 to l do
i f(j-1)
while (p(j) <> p(j+1) and (i>0) do i f(i)
if (p(j) <> p(j+1) and (i=0)
then f(j) 0
else f(j) i+1
Observatii
Algoritmul KMP presupune precompilarea sablonului, ceea ce este justificat daca M « N, adica textul este considerabil mai lung decit sablonul;
Algoritmul KMP nu decrementeaza indexul din sir, proprietate folositoare mai ales pentru cautarile pe suport extern (in fisiere);
Algoritmul KMP da rezultate bune daca o nepotrivire a aparut dupa o identificare partiala de o anumita lungime; numai in acest caz se sar caractere din sablon. In cazul in care aceste situatii sint o exceptie, algoritmul nu aduce imbunatatiri semnificative;
Algoritmul KMP imbunatateste timpul cazului cel mai nefavorabil, dar nu si timpul mediu. Algoritmul Boyer-Moore, prezentat in continuare, amelioreaza timpul mediu de cautare.
5 Algoritmul Boyer-Moore
Daca intoarcerea in text nu este dificila, o metoda mai rapida poate fi dezvoltata prin inspectarea sablonului de la dreapta la stinga in identificarea cu sirul.
Ideea este sa decidem ce trebuie facut pe baza caracterului ce a determinat nepotrivirea intre text si sablon. Pasul de prelucrare consta in a decide, pentru fiecare caracter posibil ce apare in text, actiunea care trebuie executata in cazul cind acest caracter provoaca nepotrivirea.
Exemplu:
UN EXEMPLU DE CAUTARE RAPIDA
UTARE
UTARE
UTARE
UTARE
UTARE
Se incepe compararea de la dreapta la stinga intre sablon si sir. In cazul aparitiei unei nepotriviri, pentru un caracter din sir care nu apare in sablon, deplasam sablonul cu totul la dreapta, dupa acel caracter. Pentru o nepotrivire aparuta pe un caracter din sir care este continut in sablon, deplasam sablonul pina la suprapunerea caracterelor identice, i.e. caracterul din sir care a generat nepotrivirea peste aparitia acelui caracter in sablon. Pentru cazul particular din exemplu, metoda gaseste identificarea sablonului in sir prin compararea a 4 caractere (care au generat nepotriviri) + 5 caractere ale sablonului care duc la identificare.
5.1 Implementarea algoritmului
Se initializeaza un vector skip, care arata, pentru fiecare caracter din alfabet, cit de mult se sare (se deplaseaza sablonul la dreapta) in sir daca acest caracter a provocat nepotrivirea. Trebuie sa existe o intrare pentru fiecare caracter posibil din text. Pentru simplificare, sa presupunem existenta unei functii index, ce ia ca argument un char si intoarce i pentru a i‑a litera din alfabet. Presupunem de asemenea existenta unei rutine initskip, care initializeaza vectorul skip la M (cu M lungimea sablonului) pentru caracterele ce nu sint in sablon. Pentru pentru caracterele din sablon, adica pentru 0 j M-1, initializarea lui skip se face dupa relatia:
skip[index(p[j])] = M-j-1
In aceste conditii functia de identificare este:
int caut_BM(char *p, char*a)
Daca tabela skip ar fi toata 0, acest algoritm ar corespunde unei versiuni de la stinga la dreapta a algoritmului fortei brute, deoarece instructiunea i+=M-j face ca i sa ia urmatoarea pozitie in sir (pe masura ce sablonul se misca de la stinga la dreapta peste text); apoi j=M-1 reseteaza contorul in sablon pentru a-l pregati pentru identificarea de la dreapta la stinga.
In realitate, skip foloseste la a muta sablonul la dreapta cu M caractere (de cele mai multe ori, caci daca sablonul e mult mai scurt decit textul, marea majoritate a componentelor lui skip vor avea valoarea M).
Observatie:
In cazul in care caracterul care a produs o nepotivire este prezent de mai multe ori in sablon, trebuie sa folosim aparitia sa cea mai din dreapta, deci skip trebuie construit in consecinta.
Boyer si Moore au sugerat de fapt combinarea a doua metode pentru a afla exact cu cit trebuie deplasat la dreapta sirul: metoda de mai sus, si, in plus, metoda cu vectorul next, in varianta de la dreapta la stinga, pentru ca apoi sa se aleaga in skip cea mai mare valoare. In conditiile acestei modificari, este valabila urmatoarea proprietate.
Proprietate: Algoritmul Boyer-Moore face cel mult M+N comparatii de caractere si foloseste N/M pasi, daca alfabetul nu este mic si sablonul este scurt.