|
|
|
Grupuri. Izomorfisme de grupuri
1.
a) Fie 
. Sa se arate ca 
este grup abelian unde
.
b)
Sa se
arate ca este izomorf cu
grupurile 
si 
.
c)
Sa se
calculeze 
.
d)
Sa se
demonstreze ca este izomorf cu 
2.
Sa se
rezolve ecuatia 
stiind ca
multimea solutiilor sale este grup fata de operatia 
3.
Demonstrati
ca 
este grup abelian unde
.
4.
a) Sa se arate ca este grup abelian unde
.
b)
Sa se
determine m,n astfel incat functia 
sa fie izomorfism
de la la .
c)
Sa se
calculeze .
5.
Fie 
si 
. Demonstrati ca 
este grup abelian
izomorf cu .
6.
Sa se
arate ca 
este grup abelian
izomoef cu 
prin functia 
unde 
7.
Daca 
si 
sa se demonstreze
ca:
a)
este grup abelian.
b)
, prin 
.
c)
Sa se
calculeze .
8.
Fie 
, n impar, si 
Sa se demonstreze
ca:
a)
este grup abelian.
b)
9.
Daca 
si 
Sa se arate
ca 
este grup abelian .
10.
Fie
multimile 
, 
si legile 
respectiv 
. Aratati ca 
sunt grupuri izomorfe.
11.
Fie 
si 
iar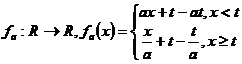 
, 
. Demonstrati ca 
este grup.
12.
Fie 
. Demonstrati ca este grup abelian.
13.
Fie 
si 
. Sa se arate ca si 
sunt grupuri izomorfe.
14.
Daca 
sa se arate
ca 
este grup abelian
si ca 
.
Grupuri de matrici
1.
Fie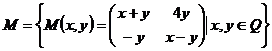 
. Sa se arate ca 
este grup abelian.
2. Sa se arate ca:
a)
Multimea
formeaza grup
abelian impreuna cu operatia de inmultire a matricilor.
b)
Este acest
grup izomorf cu 
?
3.
Fie
multimea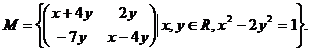 
Sa se arate ca 
este grup.
4. Se considera:
, 
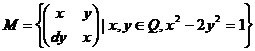unde d este un
numar liber de patrate.
Sa
se arate ca 
si 
sunt grupuri abeliene
izomorfe.
5.
Sa se
determine 
astfel incat 
sa fie grup,
daca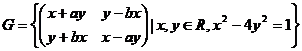 
.
6.
Fie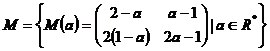 
. Sa se arate ca este grup izomorf cu 
.
7. Fie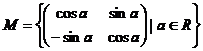 
. Sa se arate ca
este grup abelian
izomorf cu 
unde 
8.
Fie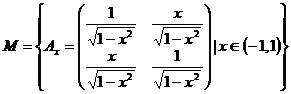 
. Demonstrati ca este grup abelian.
9.
Fie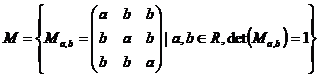 
. Sa se arate ca este grup abelian.
10.
Sa se
determine 
astfel incat sa fie grup, unde
.
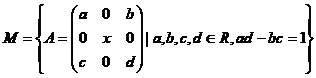11.
Fie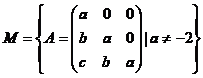 
si operatia 
. Sa se arate ca este grup.
12.
Fie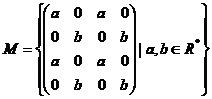 
. Sa se arate ca este grup.
13.
Fie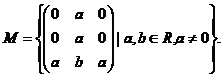 
Sa se arate
ca este grup.
14.
Fie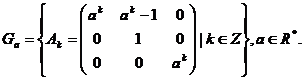 
Aratati ca 
este grup izomorf cu 
