
|
|
|
Spatiul si timpul
Ideile actuale asupra miscarii corpurilor dateaza de la Galilei si Newton. Inaintea lor oamenii il credeau pe Aristotel, care spunea ca starea naturala a unui corp era in repaus si ca el se misca numai actionat de o forta sau de un impuls. Rezulta ca un corp greu trebuie sa cada mai repede decat unul usor, deoarece ar fi fost atras mai mult spre pamant.
Traditia aristoteliana considera, de asemenea, ca toate legile care guverneaza universul pot fi elaborate doar prin gandire pura: nu era necesar sa se verifice prin observatie. Astfel, nimeni pana la Galilei nu s-a deranjat sa vada daca intr-adevar corpurile cu greutati diferite cad cu viteze diferite. Se spune ca Galilei a demonstrat ca parerea lui Aristotel era falsa, lasand sa cada greutati din turnul inclinat din Pisa. Povestea este aproape sigur neadevarata, dar Galilei a facut ceva echivalent: el a lasat sa se rostogoleasca bile cu greutati diferite pe o panta neteda. Situatia este similara aceleia a unor corpuri grele care cad vertical, dar este mai usor de observat deoarece vitezele sunt mai mici. Masurarile lui Galilei au aratat ca fiecare corp si-a marit viteza cu aceeasi valoare, indiferent de greutatea sa. De exemplu, daca lasati sa mearga o bila pe o panta care coboara cu un metru la fiecare 10 metri lungime, bila se va deplasa in josul pantei cu o viteza de circa un metru pe secunda dupa o secunda, de doi metri pe secunda dupa doua secunde s.a.m.d., indiferent cat de grea este bila. Desigur, o greutate de plumb ar cadea mai repede decat o pana, dar aceasta numai pentru ca o pana este incetinita de rezistenta aerului. Daca se lasa sa cada doua corpuri care nu intampina o rezistenta mare a aerului, cum ar fi doua greutati diferite de plumb, ele cad la fel.
Masurarile lui Galilei au fost utilizate de Newton ca baza pentru legile miscarii. In experimentele lui Galilei, atunci cand un corp se rostogolea pe panta, el era actionat intotdeauna de aceeasi forta (greutatea sa) si efectul era ca viteza sa crestea constant. Aceasta arata ca efectul real al unei forte este intotdeauna modificarea vitezei unui corp, nu acela de a-l pune in miscare, asa cum se credea anterior. Aceasta mai insemna ca ori de cate ori asupra unui corp nu actioneaza o forta, el isi va mentine miscarea in linie dreapta cu aceeasi viteza. Aceasta idee a fost pentru prima data enuntata explicit de Newton in lucrarea sa Principia Mathematica publicata in 1687, si este cunoscuta ca legea intaia a lui Newton. Legea a doua a lui Newton explica ce se intampla cu un corp atunci cand asupra sa actioneaza o forta. Aceasta afirma ca un corp va accelera, sau viteza lui se va modifica, cu o valoare proportionala cu forta. (De exemplu, acceleratia este de doua ori mai mare, daca forta este de doua ori mai mare). De asemenea, acceleratia este de atatea ori mai mica de cate ori este mai mare masa (sau cantitatea de materie) a corpului. (Aceeasi forta care actioneaza asupra unui corp cu masa dubla va produce jumatate din acceleratie). Un exemplu familiar este dat de un automobil: cu cat este mai puternic motorul, cu atat este mai mare acceleratia, dar cu cat este mai greu automobilul, cu atat este mai mica acceleratia, pentru acelasi motor.
In plus fata de legile miscarii, Newton a descoperit o lege care descrie forta de gravitatie; aceasta afirma ca fiecare corp atrage orice alt corp cu o forta proportionala cu masa fiecarui corp. Astfel, forta dintre doua corpuri va fi de doua ori mai puternica daca unul dintre corpuri (sa spunem, corpul A) are masa de doua ori mai mare. Acest lucru este de asteptat deoarece se poate considera ca noul corp A este format din doua corpuri cu masa initiala. Fiecare ar atrage corpul B cu forta initiala. Astfel, forta totala dintre A si B ar fi de doua ori forta initiala. si daca, sa presupunem, unul dintre corpuri avea de doua ori masa initiala si celalalt avea de trei ori masa sa initiala, atunci forta ar fi de sase ori mai puternica. Se poate vedea acum de ce toate corpurile cad la fel: un corp cu greutatea dubla va avea o forta de gravitatie dubla care-l trage in jos, dar va avea si masa dubla. Conform legii a doua a lui Newton, aceste doua efecte se vor anula unul pe celalalt, astfel ca acceleratia va fi aceeasi in toate cazurile.
Legea gravitatiei a lui Newton ne mai spune ca atunci cand corpurile sunt mai departate, forta este mai mica. Legea gravitatiei a lui Newton spune ca atractia gravitationala a unei stele este exact un sfert din aceea a unei stele similare aflata la jumatatea distantei. Aceasta lege prezice cu mare precizie orbitele pamantului, lunii si planetelor. Daca legea ar fi ca atractia gravitationala a unei stele scade mai rapid cu distanta, orbitele planetelor nu ar fi eliptice, ele ar fi spirale spre soare. Daca ea ar scadea mai lent, fortele gravitationale ale stelelor departate ar predomina fata de aceea a pamantului.
Marea diferenta dintre ideile lui Aristotel si acelea ale lui Galilei si Newton este ca Aristotel credea intr-o stare preferentiala de repaus, pe care orice corp ar trebui s-o aiba daca nu s-ar actiona asupra sa cu o forta sau un impuls. In particular, el credea ca pamantul era in repaus. Dar din legile lui Newton rezulta ca nu exista un criteriu unic al repausului. Se poate spune tot asa de bine ca, sa presupunem, corpul A era in repaus si corpul B in miscare cu viteza constanta in raport cu corpul A, sau corpul B era in repaus si corpul A era in miscare. De exemplu, daca se lasa deoparte pentru moment rotatia pamantului si miscarea pe orbita in jurul soarelui, se poate spune ca pamantul era in repaus si ca un tren de pe pamant se deplasa spre nord cu nouazeci de mile pe ora sau ca trenul era in repaus si ca pamantul era in miscare spre sud cu145 Km pe ora. Daca se efectueaza experimente cu corpuri in miscate in tren, toate legile lui Newton sunt de asemenea valabile. De exemplu, jucand ping-pong in tren, s-ar gasi ca mingea asculta de legile lui Newton exact ca o minge pe o masa de langa calea ferata. Astfel nu exista nici o modalitate de a spune cine se misca: trenul sau pamantul.
Lipsa unui criteriu absolut pentru repaus inseamna ca nu se poate determina daca doua evenimente care au loc la momente diferite se produc in aceeasi pozitie in spatiu. De exemplu, sa presupunem ca mingea de pingpong din tren salta in sus si in jos, lovind masa de doua ori in acelasi loc la distanta de o secunda. Pentru cineva de langa calea ferata cele doua salturi ar parea ca au loc la patruzeci de metri distanta, deoarece aceasta este distanta parcursa de tren pe calea ferata, intre salturi. Prin urmare, inexistenta unui repaus absolut inseamna ca nu se poate da unui eveniment o pozitie absoluta in spatiu asa cum credea Aristotel. Pozitiile evenimentelor si distantele dintre ele ar fi diferite pentru o persoana din tren si una de linga calea ferata si nu ar exista un motiv pentru a prefera pozitia unei persoane sau a celeilalte.
Newton a fost foarte ingrijorat de aceasta lipsa a pozitiei absolute, sau a spatiului absolut asa cum a fost numit, deoarece ea nu era in concordanta cu ideea sa despre un Dumnezeu absolut. De fapt, el a refuzat sa accepte lipsa unui spatiu absolut, chiar daca aceasta era o consecinta a legilor sale. Pentru aceasta credinta irationala el a fost sever criticat de multi, cel mai notabil fiind episcopul Berkeley, un filozof care credea ca toate obiectele materiale si spatiul si timpul sunt o iluzie. Cand faimosului dr. Johnson i s-a spus despre parerea lui Berkeley, el a strigat "O resping astfel" si a facut un gest de strivire cu piciorul pe o piatra mare.
Atat Aristotel cat si Newton credeau in timpul absolut. Adica, ei credeau ca intervalul de timp dintre doua evenimente se poate masura fara ambiguitati si ca acest timp ar fi acelasi indiferent cine l-ar masura, cu conditia sa aiba un ceas bun. Timpul era complet separat de spatiu si independent de acesta. Majoritatea oamenilor ar spune ca acesta este un punct de vedere de bun simt. Totusi, trebuie sa ne schimbam parerile despre spatiu si timp. Desi aparent notiunile noastre de bun simt actioneaza corect cand se trateaza obiecte ca merele, sau planetele, care se deplaseaza relativ lent, ele nu mai actioneaza pentru obiecte care se deplaseaza cu sau aproape de viteza luminii.
Faptul ca lumina se propaga cu o viteza finita, dar foarte mare, a fost descoperit prima oara in 1686 de astronomul danez Ole Christensen Roemer. El a observat ca timpii in care satelitii lui Jupiter treceau in spatele lui Jupiter nu erau egal distantati, asa cum ar fi de asteptat daca satelitii s-ar deplasa in jurul lui Jupiter cu viteza constanta. Deoarece pamantul si Jupiter se deplaseaza pe orbite in jurul Soarelui, distanta dintre ele variaza. Roemer a observat ca eclipsele satelitilor lui Jupiter apareau cu atat mai tarziu cu cat noi eram mai departe de Jupiter. El a argumentat ca acest lucru se intampla deoarece lumina provenita de la sateliti are nevoie de mai mult timp pentru a ajunge la noi atunci cand suntem mai departe. Totusi, masurarile variatiilor distantei dintre pamant si Jupiter, facute de el, nu erau foarte precise, astfel ca valoarea sa pentru viteza luminii era de 225 000 km pe secunda, fata de valoarea moderna de 300 000 km pe secunda. Cu toate acestea, realizarea lui Roemer, care nu numai ca a dovedit ca lumina se propaga cu viteza finita dar a si masurat acea viteza, a fost remarcabila aparand cu unsprezece ani inainte ca Newton sa publice Principia Mathematica.
O teorie corecta a propagarii luminii nu a aparut pana in 1865 cand fizicianul britanic James Clerk Maxwell a reusit sa unifice teoriile partiale care fusesera utilizate pana atunci pentru descrierea fortelor electricitatii si magnetismului. Ecuatiile lui Maxwell precizau ca in campul combinat electromagnetic puteau exista perturbatii ondulatorii si acestea se propagau cu viteza fixa, ca undele dintr-un bazin. Daca lungimea de unda a acestora (distanta dintre doua varfuri succesive ale undei) este de un metru sau mai mare, ele sunt ceea ce acum numim unde radio. Pentru lungimi de unda mai mici de cativa centimetri, ele se numesc microunde sau infrarosii (mai mari decat a zecea mia parte dintr-un centimetru). Lumina vizibila are o lungime de unda intre a patruzecea mia parte si a optzecea mia parte dintr-un centimetru. Pentru lungimi de unda si. mai scurte, ele se numesc raze ultraviolete, X si gamma.
Teoria lui Maxwell prezicea ca undele radio sau luminoase trebuie sa se deplaseze cu o anumita viteza fixa. Din teoria lui Newton el eliminase ideea de repaus absolut, astfel ca daca se presupunea ca lumina se deplaseaza cu viteza fixa, trebuie sa se indice si in raport cu ce trebuie masurata acea viteza fixa. Prin urmare s-a sugerat ca exista o substanta numita "eter" care exista peste tot chiar in spatiul "gol". Undele de lumina trebuie sa se deplaseze prin eter asa cum undele sonore se deplaseaza in aer si viteza lor trebuie deci sa fie in raport cu eterul. Diferiti observatori, care se deplaseaza in raport cu eterul, ar vedea lumina venind spre ei cu viteze diferite, dar viteza luminii in raport cu eterul ar ramane fixa. In particular, atunci cand pamantul se misca prin eter pe orbita sa in jurul soarelui, viteza luminii masurata in directia miscarii pamantului prin eter (cand noi ne miscam spre sursa de lumina) trebuie sa fie mai mare decat viteza luminii pe o directie perpendiculara fata de directia miscarii (cand noi nu ne miscam spre sursa). In 1887 Albert Michelson (care apoi a devenit primul american ce a primit premiul Nobel pentru fizica) si Edward Morley au efectuat un experiment foarte atent la Case School of Applied Science din Cleveland. Ei au comparat viteza luminii in directia miscarii pamantului cu aceea in directia perpendiculara pe cea a miscarii pamantului. Spre marea lor surpriza, au gasit ca ele sunt aceleasi!
Intre 1887 si 1905 au fost cateva incercari, cea mai notabila a fizicianului olandez Hendrik Lorentz, pentru a explica rezultatul experimentului Michelson-Morley prin obiecte care se contracta si ceasuri care raman in urma atunci cand se misca prin eter. Totusi, intr-o faimoasa lucrare din 1905, un functionar pana atunci necunoscut din biroul elvetian de patente, Albert Einstein, a aratat ca intreaga idee a eterului nu era necesara, cu conditia sa se abandoneze ideea timpului absolut. O atitudine similara a fost luata cateva saptamani mai tarziu de un matematician francez de prima marime, Henri Poincaré. Argumentele lui Einstein erau mai aproape de fizica decat acelea ale lui Poincaré care considera ca problema este matematica. De obicei noua teorie i se atribuie lui Einstein, dar Poincaré este amintit ca avand numele legat de o parte importanta a sa.
Postulatul fundamental al teoriei relativitatii, cum a fost numita, era ca legile stiintei trebuie sa fie aceleasi pentru orice observatori care se misca liber, indiferent de viteza lor. Acest lucru era adevarat pentru legile miscarii ale lui Newton, dar acum ideea a fost dezvoltata pentru a include teoria lui Maxwell si viteza luminii; toti observatorii trebuie sa masoare aceeasi viteza a luminii, indiferent cit de repede se misca ei. Aceasta idee simpla are unele consecinte remarcabile. Probabil cele mai bine cunoscute sunt echivalenta masei si energiei, exprimata de faimoasa ecuatie a lui Einstein: E = mc2 (unde E este energia, m este masa si c este viteza luminii) si legea ca nici un corp nu se poate deplasa mai repede decat viteza luminii. Datorita echivalentei energiei si masei, energia pe care o are un corp datorita miscarii sale se va adauga masei sale. Cu alte cuvinte, va face sa fie mai greu sa i se mareasca viteza. In realitate acest efect este semnificativ numai pentru obiecte care se misca cu viteze apropiate de viteza luminii. De exemplu, la 10% din viteza luminii, masa unui obiect este cu numai 0,5% mai mare decat in mod normal, in timp ce la 90% din viteza luminii ea ar fi de mai mult de doua ori masa lui normala. Atunci cand un obiect se apropie de viteza luminii, masa lui creste si mai rapid, astfel incat este necesara din ce in ce mai multa energie pentru a-i mari viteza. De fapt, el nu poate atinge viteza luminii, deoarece masa lui ar deveni infinita si, prin echivalenta energiei si masei, ar trebui o cantitate infinita de energie pentru a realiza aceasta. De aceea, orice obiect normal este intotdeauna limitat de relativitate sa se miste cu viteze mai mici decat viteza luminii. Numai lumina sau alte unde care nu au masa intrinseca se pot deplasa cu viteza luminii.
O consecinta tot atat de remarcabila a relativitatii este modul in care ea a revolutionat ideile noastre despre spatiu si timp. In teoria lui Newton, daca un impuls de lumina este trimis dintr-un loc in altul, diferiti observatori ar fi de acord asupra timpului necesar pentru acea deplasare (deoarece timpul este absolut), dar nu vor fi de acord intotdeauna asupra distantei parcurse de lumina (deoarece spatiul nu este absolut). Deoarece viteza luminii este raportul dintre distanta pe care a parcurs-o si timpul necesar pentru aceasta, observatori diferiti vor masura viteze diferite ale luminii. Pe de alta parte, in relativitate, toti observatorii trebuie sa fie de acord asupra vitezei luminii. Totusi, ei tot nu sunt de acord asupra distantei pe care a parcurs-o lumina, astfel ca acum ei nu trebuie deci sa fie de acord nici asupra timpului necesar pentru aceasta. (Timpul reprezinta raportul dintre distanta pe care a parcurs-o lumina asupra careia observatorii nu sunt de acord si viteza luminii asupra careia ei sunt de acord.) Cu alte cuvinte, teoria relativitatii pune capat ideii timpului absolut! Reiese ca fiecare observator trebuie sa aiba propria masura a timpului, inregistrata de un ceas pe care il poarta cu el si ca ceasuri identice purtate de observatori diferiti nu vor fi, in mod necesar, de acord.
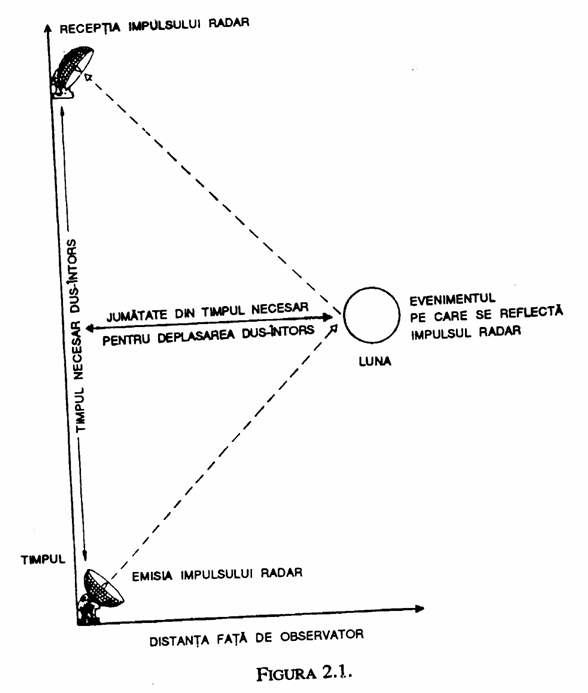
Fiecare observator poate utiliza radarul pentru a spune unde si cand are loc un eveniment, trimitand un impuls de lumina sau unde radio. O parte din impuls se reflecta inapoi la locul de producere a evenimentului si observatorul masoara timpul dupa care primeste ecoul. Atunci se spune ca timpul producerii evenimentului este exact la mijloc, intre momentul trimiterii impulsului si momentul primirii undelor reflectate; distanta la care se produce evenimentul este jumatate din timpul pentru aceasta deplasare dus-intors inmultit cu viteza luminii. (In acest sens, un eveniment este ceva care are loc intr-un singur punct in spatiu, intr-un moment specificat.) Aceasta idee este prezentata in figura 2.1, care reprezinta un exemplu de diagrama spatiu-timp. Utilizand acest procedeu, observatorii care se misca unii fata de altii vor atribui timpi diferiti si pozitii diferite aceluiasi eveniment. Nici o masurare a unui anumit observator nu este mai corecta decat o masurare a altui observator, dar toate masurarile sunt corelate. Orice observator poate calcula precis ce timp si ce pozitie va atribui evenimentului oricare alt observator, cu conditia sa stie viteza relativa a celuilalt observator.
Astazi noi utilizam aceasta metoda pentru a masura precis distantele, deoarece putem masura timpul mai precis decat lungimea. De fapt, metrul este definit ca fiind distanta parcursa de lumina in 0,000000003335640952 secunde, masurate cu un ceas cu cesiu. (Explicatia acestui numar este ca el corespunde definitiei istorice a metrului in functie de doua semne pe o anumita bara de platina tinuta la Paris.) De asemenea, putem utiliza o unitate de lungime noua, mai convenabila, numita secunda-lumina. Aceasta este definita simplu ca fiind distanta parcursa de lumina intr-o secunda. In teoria relativitatii, definim acum distanta in functie de timp si viteza luminii, astfel ca rezulta automat ca fiecare observator va masura aceeasi viteza a luminii (prin definitie, 1 metru pe 0,000000003335640952 secunde). Nu este nevoie sa se introduca ideea de eter, a carui prezenta oricum nu poate fi detectata asa cum a aratat experimentul Michelson Morley. Totusi, teoria relativitatii ne forteaza sa ne schimbam fundamental ideile despre spatiu si timp. Trebuie sa acceptam ca timpul nu este complet separat si independent de spatiu, ci se combina cu acesta formand un obiect numit spatiu-timp.
Este bine cunoscut ca pozitia unui punct in spatiu poate fi descrisa de trei numere, sau coordonate. De exemplu, se poate spune ca un punct dintr-o camera se gaseste la doi metri fata de un perete, la un metru de altul si un metru si jumatate deasupra podelei. Sau se poate stabili ca un punct era la o anumita latitudine si longitudine si la o anumita inaltime deasupra nivelului marii. Se pot utiliza oricare trei coordonate adecvate, desi ele au doar un domeniu limitat de valabilitate. Nu s-ar putea specifica pozitia lunii printr-un numar de kilometri la nord si la vest de Piccadilly Circus si la un numar de metri deasupra nivelului marii. In schimb, ea se poate descrie prin distanta fata de soare, distanta fata de planul orbitelor planetelor si unghiul dintre linia care uneste luna si soarele si linia care uneste soarele cu o stea apropiata cum ar fi Alpha Centauri. Chiar aceste coordonate nu ar fi de mare folos pentru descrierea pozitiei soarelui in galaxia noastra sau a pozitiei galaxiei noastre in grupul local de galaxii. De fapt, intregul univers se poate descrie printr-o colectie de zone care se suprapun. In fiecare zona, pentru a specifica pozitia unui punct se poate utiliza un set diferit de trei coordonate.
Un eveniment este ceva care se intampla intr-un anumit punct din spatiu si intr-un anumit moment. Astfel, el poate fi specificat prin patru numere sau coordonate. si aici, alegerea coordonatelor este arbitrara; se pot utiliza oricare trei coordonate spatiale bine definite si oricare masura a timpului. In teoria relativitatii nu exista o distinctie reala intre coordonatele spatiale si temporale exact asa cum nu exista o diferenta reala intre oricare doua coordonate spatiale. Se poate alege un set nou de coordonate in care, sa spunem, prima coordonata spatiala era o combinatie intre prima si a doua dintre vechile coordonate spatiale. De exemplu, in loc de a masura pozitia unui punct de pe pamant prin distanta in kilometri la nord de Piccadilly si la vest de Piccadilly se poate utiliza distanta in kilometri la nord-est de Piccadilly si la nord-vest de Piccadilly. Asemanator, in teoria relativitatii se poate utiliza o noua coordonata temporala care era vechiul timp (in secunde) plus distanta (in secunde-lumina) la nord de Piccadilly.
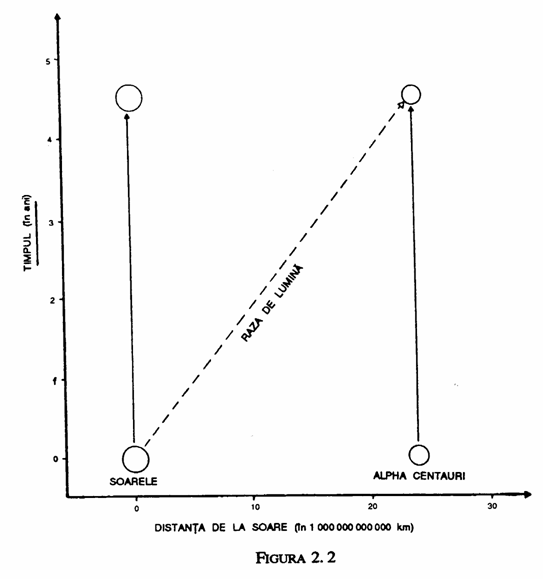
Adesea este util sa se ia in considerare cele patru coordonate ce specifica pozitia sa intr-un spatiu cvadridimensional numit spatiu-timp. Este imposibil sa se imagineze un spatiu cvadri-dimensional. Mie personal mi se pare destul de greu sa vizualizez spatiul tri-dimensional! Totusi, este usor sa se traseze diagrame ale spatiilor bidimensionale, cum este suprafata pamantului. (Suprafata pamantului este bi-dimensionala deoarece pozitia unui punct poate fi specificata prin doua coordonate, latitudine si longitudine.) in general, eu voi utiliza diagrame in care timpul creste in sus si una din dimensiunile spatiale este prezentata orizontal. Celelalte doua dimensiuni spatiale sunt ignorate sau, uneori, una din ele este indicata in perspectiva. (Acestea se numesc diagrame spatio-temporale, cum este figura 2.1.) De exemplu, in figura 2.2 timpul se masoara pe verticala in ani si distanta de-a lungul liniei de la soare la Alpha Centauri se masoara pe orizontala in kilometri. Traiectoriile soarelui si Alpha Centauri in spatiu si timp sunt prezentate ca linii verticale in stanga si in dreapta diagramei. O raza de lumina de la soare urmeaza a linie diagonala si are nevoie de patru ani pentru a ajunge de la soare la Alpha Centauri.
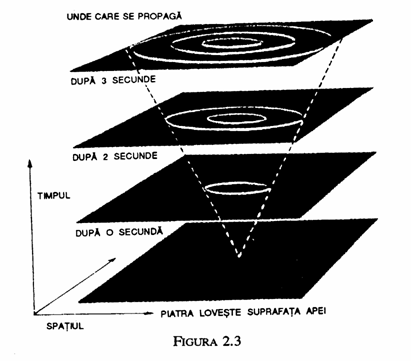
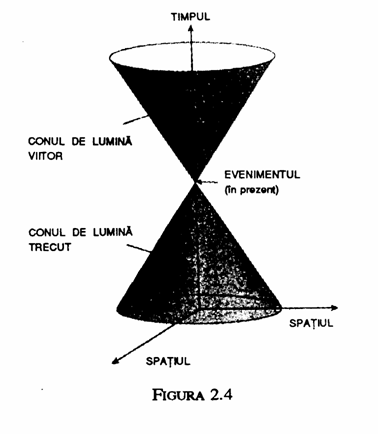
Asa cum am vazut, ecuatiile lui Maxwell preziceau ca viteza luminii trebuie sa fie aceeasi indiferent de viteza sursei, si acest lucru a fost confirmat de masurari precise. Rezulta din aceasta ca daca se emite un impuls de lumina la un anumit moment si intr-un anumit punct din spatiu, atunci pe masura ce trece timpul el se va imprastia ca o sfera de lumina ale carei dimensiune si pozitie sant independente de viteza sursei. Dupa o milionime de secunda lumina se va imprastia formand o sfera cu raza de 300 metri; dupa doua milionimi de secunda, raza va fi de 600 metri s.a.m.d. Va fi la fel ca undele care se raspandesc pe suprafata unui bazin cand se arunca o piatra in apa. Undele se raspandesc ca un cerc ce devine tot mai mare cu trecerea timpului. Daca se considera un model tri-dimensional care consta din suprafata bidimensionala a bazinului si o dimensiune a timpului,cercul de unde in expansiune va marca un con cu varful in locul si timpul in care piatra a lovit apa (fig: 2.3). Asemanator, lumina care se raspandeste de la un eveniment formeaza un con tridimensional in spatiu-timpul cvadri-dimensional. Acest con se numeste conul de lumina viitor al evenimentului. In acelasi fel putem trasa un alt con, numit conul de lumina trecut, care reprezinta setul de evenimente din care impulsul de lumina poate ajunge la evenimentul dat (fig. 2.4).
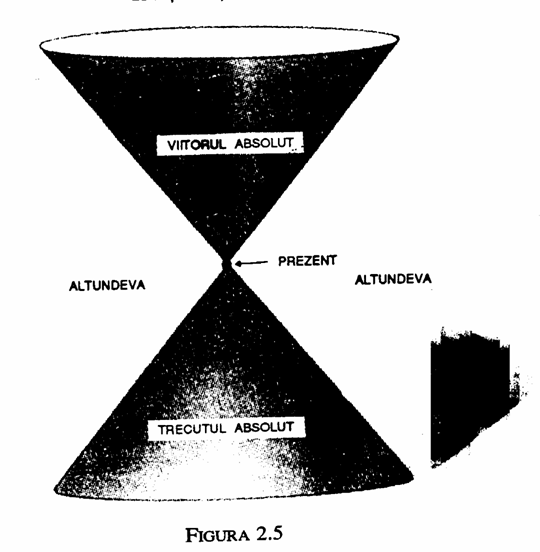
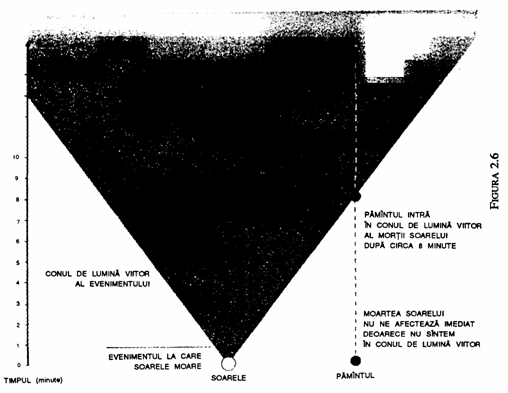
Conurile de lumina trecut si viitor ale evenimentului p impart spatiul-timpul in trei regiuni (fig. 2.5). Viitorul absolut al evenimentului este regiunea din interiorul conului de lumina viitor al lui P. EI este setul tuturor evenimentelor care pot fi afectate de ceea ce se intampla in P. Evenimentele din afara conului de lumina al lui P nu pot fi ajunse de semnalele din P deoarece nimic nu se deplaseaza mai repede decat lumina. Prin urmare ele nu pot fi influentate de ceea ce se intampla in P. Trecutul absolut al lui P este regiunea din interiorul conului de lumina trecut. El este setul tuturor evenimentelor ale caror semnale care se deplaseaza la sau sub viteza luminii pot ajunge in P. El este setul tuturor evenimentelor care pot afecta ceea ce se intampla in P. Daca se cunoaste ceea ce se intampla la un anumit moment undeva intr-o regiune a spatiului care se gaseste in conul de lumina trecut al lui P, se poate prezice ce se va intampla in P. Restul reprezinta regiunea de spatiu-timp care nu se gaseste in conurile de lumina viitor sau trecut ale lui P. Evenimentele din aceasta regiune nu pot afecta sau nu pot fi afectate de evenimente din P. De exemplu, daca soarele ar inceta sa lumineze chiar in momentul de fata, el nu ar afecta obiectele de pe Pamant in momentul de fata deoarece ele s-ar gasi in regiunea din afara conului evenimentului corespunzand stingerii soarelui (fig. 2.6). Noi am sti despre aceasta numai dupa 8 minute, timpul necesar luminii sa ajunga de la soare la noi. Numai atunci evenimentele de pe Pamant s-ar gasi in conul de lumina viitor al evenimentului corespunzator stingerii soarelui. In mod asemanator, nu cunoastem ce se intampla la momente indepartate in univers; lumina pe care o vedem de la galaxiile indepartate le-a parasit acum milioane de ani si in cazul obiectelor celor mai indepartate pe care le vedem, lumina le-a parasit acum circa opt miliarde de ani. Astfel, cand privim universul, il vedem asa cum a fost in trecut.
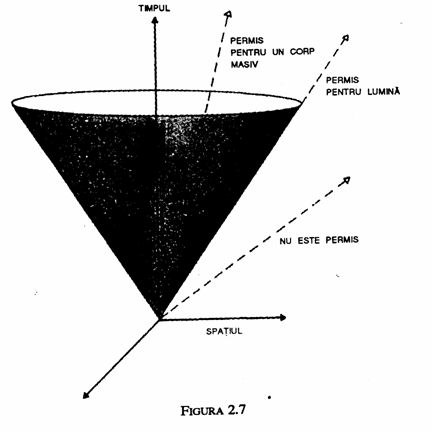
Daca se neglijeaza efectele gravitationale, asa cum au facut Einstein si Poincaré in 1905, se obtine ceea se numeste teoria speciala a relativitatii. Pentru fiecare eveniment in spatiu-timp putem construi un con de lumina (setul tuturor traiectoriilor posibile ale luminii in spatiu-timp emise de eveniment) si deoarece viteza luminii este aceeasi pentru orice eveniment si in orice directie, toate conurile de lumina vor fi identice si vor fi indreptate in aceeasi directie. Teoria mai spune ca nimic nu se poate deplasa mai repede decat lumina. Aceasta inseamna ca traiectoria oricarui obiect in spatiu si timp trebuie sa fie reprezentata printr-o linie care se gaseste in interiorul conului de lumina pentru fiecare eveniment din el (fig. 2.7).
Teoria speciala a relativitatii a reusit foarte bine sa explice ca viteza luminii apare aceeasi pentru toti observatorii (asa cum a aratat experimentul Michelson-Morley) si sa descrie ce se intampla atunci cand obiectele se misca la viteze apropiate de viteza luminii. Totusi, ea nu era compatibila cu teoria newtoniana a gravitatiei, care spune ca obiectele se atrageau unele pe altele cu o forta care depinde de distanta dintre ele. Aceasta inseamna ca daca se deplaseaza unul dintre obiecte, forta exercitata asupra celorlalte s-ar schimba instantaneu. Sau, cu alte cuvinte, efectele gravitationale s-ar deplasa cu viteza infinita, in loc sa se deplaseze la sau sub viteza luminii, asa cum cerea teoria speciala a relativitatii. Intre 1908 si 1914 Einstein a facut mai multe incercari nereusite de a gasi o teorie a gravitatiei care sa fie compatibila cu teoria speciala a relativitatii. In cele din urma, in 1915, el a propus ceea ce noi numim acum teoria generala a relativitatii.
Einstein a emis ipoteza revolutionara ca gravitatia nu este o forta ca celelalte forte, ci este o consecinta a faptului ca spatiu-timpul nu este plan, asa cum s-a presupus anterior; el este curbat, sau "infasurat", de distributia masei si energiei in el. Corpuri ca pamantul nu sunt determinate sa se miste pe orbite curbe de o forta numita gravitatie; in schimb ele urmeaza corpul cel mai apropiat printr-o traiectorie dreapta intr-un spatiu curbat, care se numeste o linie geodezica. O linie geodezica este traiectoria cea mai scurta (sau cea mai lunga) intre doua puncte apropiate. De exemplu, suprafata pamantului este un spatiu curbat bi-dimensional. O linie geodezica pe pamant se numeste un cerc mare si este ruta cea mai scurta dintre doua puncte (fig. 2.8). Deoarece linia geodezica este calea cea mai scurta intre doua aeroporturi, aceasta este ruta pe care un navigator aerian o va indica pilotului pentru zbor. In relativitatea generalizata, corpurile urmeaza intotdeauna linii drepte in spatiu-timpul cvadridimensional dar, cu toate acestea, noua ni se va parea ca se deplaseaza pe traiectorii curbe in spatiul nostru tridimensional. (Este la fel ca atunci cand se priveste un avion care zboara deasupra unui teren deluros. Desi el urmeaza o linie dreapta in spatiul tri-dimensional, urma sa parcurge o traiectorie curbata pe solul bi-dimensional.)

Masa soarelui curbeaza spatiu-timpul astfel incat desi pamantul urmeaza o linie dreapta din spatiu-timpul cvadridimensional, noua ni se pare ca se misca de-a lungul unei orbite circulare in spatiul tri-dimensional. De fapt, orbitele planetelor prezise de relativitatea generalizata sunt aproape exact aceleasi cu cele prezise de teoria newtoniana a gravitatiei. Totusi, in cazul lui Mercur care, fiind cea mai apropiata planeta de soare, simte efectele gravitationale cel mai puternic si are o orbita mai alungita, relativitatea generalizata prezice ca axa lunga a elipsei trebuie sa se roteasca in jurul soarelui cu o valoare de circa un grad in zece mii de ani. Oricat de mic este acest efect, el a fost observat inainte de 1915 si a servit drept una din primele confirmari ale teoriei lui Einstein. In ultimii ani au fost masurate cu radarul abateri chiar mai mici ale orbitelor celorlalte planete fata de prezicerile newtoniene si s-a descoperit ca sunt in concordanta cu prezicerile relativitatii generalizate.
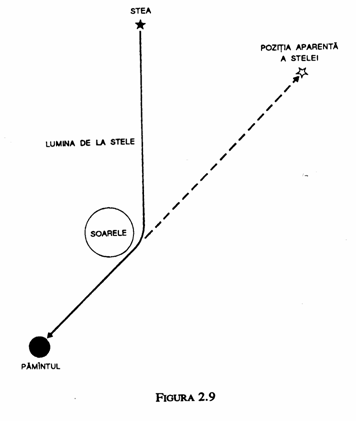
De asemenea, razele de lumina trebuie sa urmeze linii geodezice in spatiu-timp. Din nou, faptul ca spatiul este curbat inseamna ca lumina nu mai pare ca se propaga dupa linii drepte in spatiu. Astfel, relativitatea generalizata prezice ca lumina trebuie sa fie curbata de campurile gravitationale. De exemplu, teoria prezice ca conurile de lumina ale punctelor din apropierea soarelui ar fi usor curbate spre interior, datorita masei soarelui. Aceasta inseamna ca lumina unei stele indepartate care trece pe langa soare ar fi deviata cu un unghi mic, facand ca steaua sa apara intr-o pozitie diferita pentru un observator de pe pamant (fig. 2.9). Desigur, daca lumina stelei a trecut intotdeauna in apropierea soarelui, noi nu am putea spune daca lumina a fost deviata sau steaua a fost in realitate acolo unde o vedem. Totusi, atunci cand pamantul se misca in jurul soarelui, diferite stele par a trece in spatele soarelui si lumina lor este deviata. Prin urmare, ele isi schimba pozitia aparenta in raport cu celelalte stele.
In mod normal, acest efect este foarte greu de vazut, deoarece lumina soarelui face imposibila observarea stelelor care apar pe cer in apropierea soarelui. Totusi, acest lucru este posibil in timpul unei eclipse de soare, cand lumina soarelui este blocata de luna. Prezicerea lui Einstein privind devierea luminii nu a putut fi testata imediat in 1915, deoarece era in timpul primului razboi mondial si abia in 1919 o expeditie britanica, ce a observat o eclipsa din vestul Africii, a aratat ca intr-adevar lumina a fost deviata de soare, exact asa cum a prezis teoria. Aceasta verificare a unei teorii germane de oameni de stiinta britanici a fost salutata ca un act maret de reconciliere intre cele doua tari dupa razboi. De aceea, este o ironie ca o examinare ulterioara a fotografiilor luate de acea expeditie a aratat ca erorile erau tot atat de mari ca si efectul pe care incercau sa-l masoare. Masurarea lor a fost un noroc pur, sau un caz de cunoastere a rezultatului pe care au dorit sa-l obtina, o intamplare care nu este neobisnuita in stiinta. Totusi, devierea luminii a fost precis confirmata de mai multe observatii ulterioare.
O alta prezicere a relativitatii generalizate este ca timpul trebuie sa para ca trece mai incet langa un corp masiv ca pamantul. Aceasta deoarece exista o relatie intre energia luminii si frecventa sa (adica numarul de unde de lumina pe secunda): cu cat este mai mare energia cu atat este frecventa mai mare. Atunci cand lumina se propaga in sus in campul gravitational ai pamantului, ea pierde energie si astfel frecventa sa scade. (Aceasta inseamna ca timpul dintre un varf al undei si urmatorul creste.) Pentru cineva aflat la inaltime ar parea ca tot ce se intampla jos necesita un timp mai lung. Aceasta prezicere a fost testata in 1962, cu ajutorul unei perechi de ceasuri foarte precise montate in varful si la baza unui turn de apa. S-a descoperit ca ceasul de la baza, care era mai aproape de pamant, mergea mai incet, in exacta concordanta cu relativitatea generalizata. Diferenta de viteza a ceasurilor la diferite inaltimi deasupra pamantului este acum de importanta practica considerabila, o data cu aparitia sistemelor de navigatie foarte precise bazate pe semnale de la sateliti. Daca se ignora prezicerile relativitatii generalizate, pozitia calculata va fi gresita cu cativa kilometri.
Legea miscarii a lui Newton pune capat ideii de pozitie absoluta in spatiu. Teoria relativitatii a renuntat la timpul absolut. Sa consideram o pereche de gemeni. Sa presupunem ca unul dintre gemeni se duce sa traiasca pe varful unui munte, iar celalalt locuieste la malul marii. Primul va imbatrani mai repede decat al doilea. Astfel, daca se intalnesc, unul va fi mai in varsta decat celalalt. In acest caz, diferenta de varsta va fi foarte mica, dar ea ar fi mult mai mare daca unul dintre gemeni pleaca intr-o calatorie lunga cu o nava spatiala care se deplaseaza cu o viteza apropiata de viteza luminii. Atunci cand se intoarce, el va fi mult mai tanar decat cel care a ramas pe pamant. Acesta se numeste paradoxul gemenilor, dar el este un paradox numai daca se considera ca timpul este absolut. In teoria relativitatii nu exista timp absolut unic, dar in schimb fiecare individ are propria sa masura a timpului care depinde de locul catre care se deplaseaza si de modul in care se deplaseaza.
Inainte de 1915, spatiul si timpul au fost considerate ca o arena fixa in care au loc evenimentele, dar care nu este afectata de ceea ce se intampla in ea. Acest lucru a fost adevarat chiar pentru teoria speciala a relativitatii: Corpurile se miscau, fortele atrageau si respingeau, dar timpul si spatiul pur si simplu continuau sa ramana neafectate. Era natural sa se considere ca spatiul si timpul se derulau la infinit.
Totusi, in teoria generala a relativitatii situatia este destul de diferita. Spatiul si timpul sunt acum marimi dinamice: atunci cand un corp se misca, sau o forta actioneaza, aceasta afecteaza curbarea spatiului si timpului si la randul sau structura spatiu-timpului afecteaza modul in care corpurile se misca si fortele actioneaza. Spatiul si timpul nu numai ca afecteaza, dar sunt afectate de orice se intampla in univers. Exact asa cum nu se poate vorbi despre evenimente din univers fara notiuni de spatiu si timp, tot asa in relativitatea generalizata nu are sens sa se vorbeasca despre spatiu si timp in afara universului.
Pentru urmatoarele decenii aceasta noua intelegere a spatiului si timpului a revolutionat imaginea noastra despre univers. Vechea idee despre universul in esenta neschimbator care a existat si continua sa existe a fost inlocuita pentru totdeauna cu notiunea de univers dinamic in expansiune care parea sa fi inceput la un moment finit in trecut si care ar putea sa se termine la un moment finit in viitor. Aceasta revolutie formeaza subiectul urmatorului capitol. Si, ani de zile mai tarziu, a fost de asemenea punctul de inceput al activitatii mele in fizica teoretica. Roger Penrose si cu mine am aratat ca teoria generala a relativitatii a lui Einstein insemna ca universul trebuie sa aiba un inceput si, posibil, un sfarsit.