|
|
|
PROBLEME DE TIMP
1. Transformarea unitatilor arc in unitati timp si invers folosind relatiile dintre ele
In lipsa unui calculator sau a unor table de transformare, retinem relatiile de transformare :
360
= 24h
24h
= 360
15
= 1h
1h
= 15
1
= 4m
1m
= 15'
1'
= 4s
1s
= 15" = 0'.25
0'.1
= 0s.4
Unitati arc in unitati timp
1.
Sa se transforme
longitudinea 
in unitati de timp.
Rezolvare:
se transcrie valoarea data in grade, minute si secunde arc
se imparte numarul de grade la 15 - partea intreaga reprezinta ore intregi iar restul reprezinta fractiuni de ora care se inmultesc cu 60 pentru a fi transformate in minute timp
la rezultatul astfel obtinut se adaoga numarul de minute intregi iar rezultatul obtinut se imparte la 15, obtinandu-se numarul de minute intregi. Restul de fractiuni de minut se inmulteste cu 60 pentru a se transforma in secunde timp
la rezultatul astfel obtinut se adauga numarul de secunde arc iar rezultatul obtinut se imparte la 15, obtinandu-se numarul de secunde timp prin rotunjire
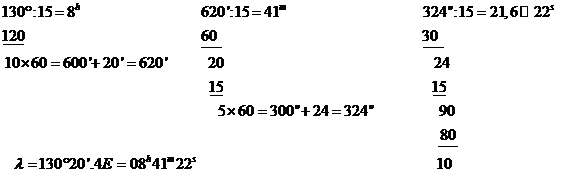
2.
Sa se transforme
longitudinea 
in unitati de timp.
R=
3.
Sa se transforme
longitudinea 
in unitati de timp.
R=
4.
Sa se transforme
longitudinea 
in unitati de timp.
R=
5.
Sa se transforme
longitudinea 
in unitati de timp.
R=
Unitati timp in unitati arc
1.
Sa se transforme in unitati arc
valoarea de timp 
Rezolvare:
inmultim separat orele, minutele si secundele cu 15 si le transformam in unitatea superioara acolo unde este cazul impartind la 60
adunam rezultatele obtinute
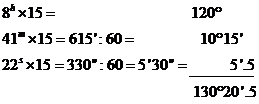
1.
Sa se transforme
in unitati arc valoarea de timp de 
R=
2.
Sa se transforme
in unitati arc valoarea de timp de 
R=
3.
Sa se transforme
in unitati arc valoarea de timp de 
R=
4.
Sa se transforme
in unitati arc valoarea de timp de 
R=
Transformarea unitatilor arc in unitati timp si invers folosind T58a si T58b
Unitati arc in unitati timp
1. Sa se transforme longitudinea in unitati de timp.
Rezolvare:
retranscriem valoarea arc in grade, minute si secunde arc
se intra succesiv in tabla T58a cu numarul de grade, apoi cu numarul de minute si apoi cu numarul de secunde si se extrag valorile corespunzatoare de unitati timp
valorile obtinute se aduna
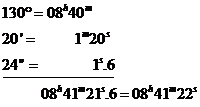
2.
Sa se transforme
longitudinea in unitati de timp.
R=
3. Sa se transforme longitudinea in unitati de timp.
R=
Unitati timp in unitati arc
1. Sa se transforme in unitati arc
valoarea de timp de
Rezolvare:
se foloseste tabla T58b intrandu-se succesiv - ore, minute si secunde
ATENTIE la faptul ca in tabla sunt inserate numai 5 ore, 59 minute si separat 59 secunde
pentru numarul de ore vom inmulti convenabil valorile din tabla corespunzator valorilor noastre. Astfel pentru 8 ore vom inmulti valoarea de la 4 ore cu 2; pentru 9 ore vom inmulti valoarea de la 3 ore cu 3; pentru 11 ore vom calcula valoarea de la 9 ore si vom adaoga valoarea de la 2 ore
adunam valorile extrase din tabla
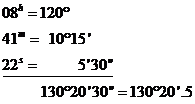
2.
Sa
se transforme in unitati arc valoarea de timp de R=
3.
Sa
se transforme in unitati arc valoarea de timp de R=
Transformarea unitatilor arc in unitati timp si invers folosind calculatorul
Unitati arc in unitati timp
1. Sa
se transforme longitudinea in unitati de timp.
Rezolvare:
tastam valoarea data pe calculator - citire calculator 130.34
impartim valoarea setata la 15 - citire calculator 8.6893333
rezultatul obtinut se transforma in grade
folosind tasta SHIFT - citire calculator 8°41°21,6 adica 
1.
Sa se transforme
longitudinea in unitati de timp.
R=
2.
Sa se transforme
longitudinea in unitati de timp.
R=
Unitati timp in unitati arc
1. Sa
se transforme in unitati arc valoarea de timp de
Rezolvare:
tastam pe calculator valoarea data in unitati timp ca si cum ar fi unitati arc - citire calculator 8,6894444
inmultim valoarea setata cu 15 - citire calculator 130.34166
rezultatul obtinut se transforma in grade folosind tasta SHIFT - citire calculator 130°20 adica 130°20
1.
Sa se transforme
in unitati arc valoarea de timp de
R=
2.
Sa se transforme in unitati arc valoarea
de timp de
R=
2. Calculul unghiului orar al unui astru la meridianul locului
1. Cunoscand
unghiul orar al Soarelui la meridianul Greenwich 
sa se determine
valoarea unghiului orar al astrului la meridianul locului 
.
Rezolvare:
relatia folosita este 
avem in vedere ca longitudinea intra cu semnul ei: daca este estica si - daca este vestica
ATENTIE la ordonarea cifrelor in tipul de calcul!
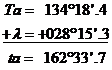
2. Cunoscand
unghiul orar al Soarelui la meridianul Greenwich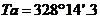 
sa se determine
valoarea unghiului orar al astrului la meridianul locului 
.
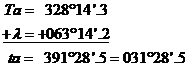
3. Cunoscand
unghiul orar al stelei ARCTURUS la meridianul Greenwich 
sa se determine
valoarea unghiului orar al astrului la meridianul locului 
.
ATENTIE!
longitudinea este vestica deci are semnul minus (-)
longitudinea este mai mare in valoare absoluta decat unghiul orar la Greenwich
unghiul orar al astrului la meridianul locului (t) se masoara de la meridianul superior al observatorului (cel care contine zenitul) pana la cercul orar al astrului si ia valori cuprinse intre 0° si 360° - CA ATARE NU ESTE NEGATIV NICIODATA!
rezulta ca vom suplimenta valoarea unghiului orar la Greenwich cu 360°
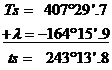
3. Calculul longitudinii fusului
a) Calculul longitudinii fusului folosind calculul matematic
Cunoscand longitudinea locului este necesar sa calculam longitudinea fusului orar in care ne aflam pentru a putea parcurge anumiti pasi in calculule de navigatie astronomica.
Pentru a afla longitudinea fusului (
) in functie de longitudinea locului (
) vom proceda astfel:
impartim valoarea longitudinii locului la 15
vom obtine un cat (C) si un rest (R)
daca restul este 
atunci 
daca restul este 
atunci 
1. Sa se determine longitudinea fusului () cunoscand ca
longitudinea locului este 
Rezolvare:
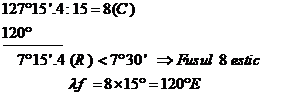
2. Sa se determine longitudinea fusului () cunoscand ca
longitudinea locului este 
Rezolvare:
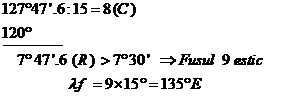
3.
Sa se determine longitudinea fusului () cunoscand ca
longitudinea locului este 
4.
Sa se determine longitudinea fusului () cunoscand ca
longitudinea locului este 
5.
Sa se determine longitudinea fusului () cunoscand ca
longitudinea locului este 
6.
Sa se determine longitudinea fusului () cunoscand ca
longitudinea locului este 
7.
Sa se determine longitudinea fusului () cunoscand ca
longitudinea locului este 
b) Calculul longitudinii fusului cu ajutorul calculatorului
3. Sa se determine
longitudinea fusului () cu ajutorul
calculatorului cunoscand ca longitudinea locului este
Rezolvare:
tastam valoarea data pe calculator - citire calculator 127.79333
impartim valoarea setata la 15 - citire calculator 8.5195555 - 8 este catul (C)
scadem numarul care reprezinta partea intreaga -8, citire calculator 0.5195555
inmultim valoarea rezultata cu 15 - citire calculator 7.7933332 - acesta este restul (R)
rezultatul obtinut se transforma in grade folosind tasta SHIFT - citire calculator 7°47°36 adica 7°47'.6
se observa ca restul obtinut este mai mare de 7°30 si ca numarul fusului este 9
.
4. Sa se determine
longitudinea fusului () cu ajutorul
calculatorului cunoscand ca longitudinea locului este 
R = 
4. Calculul timpului fusului (tf) in functie de timpul mediu la meridianul locului (tm)
1.
Sa se determine
valoarea timpului fusului pentru longitudinea 
pentru timpul mediu la meridianul locului avand
valoarea 
Rezolvare:
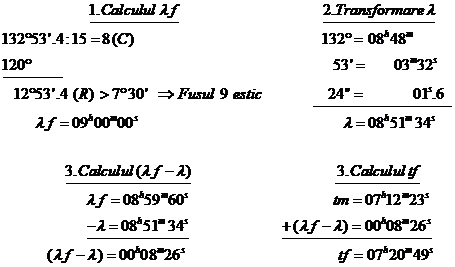
2.
Sa se determine
valoarea timpului fusului pentru longitudinea 
pentru timpul mediu la meridianul locului avand
valoarea 
3.
Sa se determine
valoarea timpului fusului pentru longitudinea 
pentru timpul mediu la meridianul locului avand
valoarea 
4.
Sa se determine
valoarea timpului fusului pentru longitudinea 
pentru timpul mediu la meridianul locului avand
valoarea 
5.
Sa se determine
valoarea timpului fusului pentru longitudinea 
pentru timpul mediu la meridianul locului avand
valoarea 
6.
Sa se determine
valoarea timpului fusului pentru longitudinea 
pentru timpul mediu la meridianul locului avand valoarea 
